POJ #1186 方程的解数 | 中途相遇法 + Hash | 解题报告

POJ #1186 - 方程的解数

时限 5000MS/Case 内存 128MB/Case

题目描述

已知一个n元高次方程：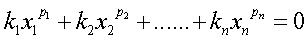 
 
其中：x1, x2,...,xn是未知数，k1,k2,...,kn是系数，p1,p2,...pn是指数。且方程中的所有数均为整数。 
假设未知数1 <= xi <= M, i=1,,,n，求这个方程的整数解的个数。 
1 <= n <= 6；1 <= M <= 150。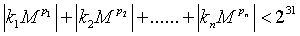 
 
方程的整数解的个数小于2³¹。 
★本题中，指数Pi(i=1,2,...,n)均为正整数。

输入格式

第1行包含一个整数n。第2行包含一个整数M。第3行到第n+2行，每行包含两个整数，分别表示ki和pi。两个整数之间用一个空格隔开。第3行的数据对应i=1，第n+2行的数据对应i=n。

输出格式

仅一行，包含一个整数，表示方程的整数解的个数。

样例输入

31501  2-1  21  2

样例输出

178

数据范围

1<=M<=150,1<=N<=6,1<=X[i]<=M

----------------------------------------------------------

题目分析

确定思路，因为这道题不好建立数学解题模型，所以直接选择上枚举算法。

枚举6个数再来检查的话时间复杂度为O(M^6)，最坏时间复杂度为O(150^6)，无法通过此题。

所以我们想到用中途相遇的思想，先枚举前3个数，把前三个数的和存起来，再枚举后三个数，得到的每一个和与前面的和进行验算，即可得到ans。

因为前半边最多能产生的和的个数为150*150*150，所以我们构建哈希表:hash[4000000]。

----------------------------------------------------------

代码(枚举过程挺渣的，好在1500ms跑完了全部测试点)

#include <iostream>#include <algorithm>#include <cstdio>#include <cstdlib>#include <cstring>#include <map>#include <set>#include <queue>#include <stack>#include <vector>#define hashsize 4000003using namespace std;long long p[151][10];struct node{int value;int count;};node h[hashsize];bool used[hashsize];int get_hash(int x){int tmp=(abs(x))%hashsize;while(used[tmp] && h[tmp].value!=x){tmp++;if(tmp>4000000) tmp%=hashsize;}return tmp;}int hash_count(int x){int i=get_hash(x);return h[i].count;}void hash_insert(int x){int i=get_hash(x);h[i].value=x;used[i]=true;h[i].count++;}int pow(int base,int power){if(p[base][power]>=1) return p[base][power];if(power==0) return 1;long long temp=pow(base,power/2);if(power%2==1) return p[base][power]=(temp*temp)*base;else return p[base][power]=(temp*temp);}void calcpow(){for(int i=1;i<=150;i++) p[i][1]=i;for(int i=1;i<=150;i++)for(int j=2;j<=9;j++) p[i][j]=p[i][j-1]*i;return;}void work(){int k[7],pow_up[7];int n,m,ans=0,tempr,cnt;scanf("%d%d",&n,&m);for(int i=1;i<=n;i++) scanf("%d%d",&k[i],&pow_up[i]);if(n==1){for(int i=1;i<=m;i++){if(pow(i,pow_up[1])*k[1]==0) ans++;}}else if(n==2){for(int i=1;i<=m;i++){for(int j=1;j<=m;j++){if(pow(i,pow_up[1])*k[1]+pow(j,pow_up[2])*k[2]==0) ans++;}}}else if(n==3){for(int i=1;i<=m;i++){for(int j=1;j<=m;j++){for(int l=1;l<=m;l++){if(pow(i,pow_up[1])*k[1]+pow(j,pow_up[2])*k[2]+pow(l,pow_up[3])*k[3]==0) ans++;}}}}else if(n==4){for(int i=1;i<=m;i++){for(int j=1;j<=m;j++){hash_insert(pow(i,pow_up[1])*k[1]+pow(j,pow_up[2])*k[2]);}}for(int i=1;i<=m;i++){for(int j=1;j<=m;j++){ans+=hash_count(-(pow(i,pow_up[3])*k[3]+pow(j,pow_up[4])*k[4]));}}}else if(n==5){for(int i=1;i<=m;i++){for(int j=1;j<=m;j++){hash_insert(pow(i,pow_up[1])*k[1]+pow(j,pow_up[2])*k[2]);}}for(int i=1;i<=m;i++){for(int j=1;j<=m;j++){for(int l=1;l<=m;l++){ans+=hash_count(-(pow(i,pow_up[4])*k[4]+pow(j,pow_up[5])*k[5]+pow(l,pow_up[3])*k[3]));}}}}else if(n==6){calcpow();for(int i=1;i<=m;i++){for(int j=1;j<=m;j++){for(int l=1;l<=m;l++){hash_insert(p[i][pow_up[1]]*k[1]+p[j][pow_up[2]]*k[2]+p[l][pow_up[3]]*k[3]);}}}for(int i=1;i<=m;i++){for(int j=1;j<=m;j++){for(int l=1;l<=m;l++){ans+=hash_count(-(p[i][pow_up[4]]*k[4]+p[j][pow_up[5]]*k[5]+p[l][pow_up[6]]*k[6]));}}}}printf("%d",ans);return;}int main(){work();return 0;}