动归---卡特兰数（栈）

题目背景

栈是计算机中经典的数据结构，简单的说，栈就是限制在一端进行插入删除操作的线性表。

栈有两种最重要的操作，即pop（从栈顶弹出一个元素）和push（将一个元素进栈）。

栈的重要性不言自明，任何一门数据结构的课程都会介绍栈。宁宁同学在复习栈的基本概念时，想到了一个书上没有讲过的问题，而他自己无法给出答案，所以需要你的帮忙。

题目描述

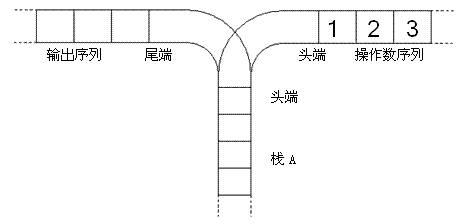
宁宁考虑的是这样一个问题：一个操作数序列，从1，2，一直到n（图示为1到3的情况），栈A的深度大于n。

现在可以进行两种操作，

1.将一个数，从操作数序列的头端移到栈的头端（对应数据结构栈的push操作）

2. 将一个数，从栈的头端移到输出序列的尾端（对应数据结构栈的pop操作）

使用这两种操作，由一个操作数序列就可以得到一系列的输出序列，下图所示为由1 2 3生成序列2 3 1的过程。

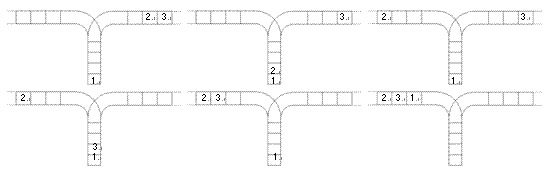
（原始状态如上图所示）

你的程序将对给定的n，计算并输出由操作数序列1，2，…，n经过操作可能得到的输出序列的总数。

输入输出格式

输入格式：

输入文件只含一个整数n（1≤n≤18）

输出格式：

输出文件只有一行，即可能输出序列的总数目

输入输出样例输出样例#1：

3         5

题解：

这是一道dp题（推倒卡特兰数）；

原问题为：序列个数为n时出栈方案数；

则子问题为：数列个数为i时的方案数；

定义状态f（i）表示数列个数为i时的方案数；

怎么写状态转移方程呢。（这有点困难）；

首先，我们设f(n)=序列个数为n的出栈序列种数。(我们假定，最后出栈的元素为k，显然，k取不同值时的情况是相互独立的，也就是求出每种k最后出栈的情况数后可用加法原则，由于k最后出栈，因此，在k入栈之前，比k小的值均出栈，此处情况有f(k-1)种，而之后比k大的值入栈，且都在k之前出栈，因此有f(n-k)种方式，由于比k小和比k大的值入栈出栈情况是相互独立的，此处可用乘法原则，f(n-k)*f(k-1)种。

首次出空之前第一个出栈的序数k将1~n的序列分成两个序列，其中一个是1~k-1，序列个数为k-1，另外一个是k+1~n，序列个数是n-k。

此时，我们若把k视为确定一个序数，那么根据乘法原理，f(n)的问题就等价于--序列个数为k-1的出栈序列种数乘以序列个数为n - k的出栈序列种数，即选择k这个序数的f(n)=f(k-1)×f(n-k)。而k可以选1到n，所以再根据加法原理，将k取不同值的序列种数相加，得到的总序列种数为:f(n)=f(0)f(n-1)+f(1)f(n-2)+……+f(n-1)f(0)。

最后，令f(0)=1，f(1)=1。

于是这道题就很简单了

状态转移方程为：f(i)= f(0)f(i-1)+f(1)f(i-2)+……+f(i-1)f(0)。

时间复杂度：o（n*n）

空间复杂度为：o（n）；

下面是程序；

#include<bits/stdc++.h>
using namespace std;
int f[19],n;
int main()
{
cin>>n;
f[0]=1;f[1]=1;//初始值 
for(int i=2;i<=n;i++)//i从2开始，防止改变前面数据 
for(int j=0,k=i-1;j<=i-1&&k>=0;j++,k--)
f[i]=f[i]+f[j]*f[k];
cout<<f[n];
}