Area pick原理+线段上格点数目+向量叉乘

Area

Time Limit: 1000MS Memory Limit: 10000KTotal Submissions: 6787 Accepted: 2928

Description

Being well known for its highly innovative products, Merck would definitely be a good target for industrial espionage. To protect its brand-new research and development facility the company has installed the latest system of surveillance robots patrolling the area. These robots move along the walls of the facility and report suspicious observations to the central security office. The only flaw in the system a competitor抯 agent could find is the fact that the robots radio their movements unencrypted. Not being able to find out more, the agent wants to use that information to calculate the exact size of the area occupied by the new facility. It is public knowledge that all the corners of the building are situated on a rectangular grid and that only straight walls are used. Figure 1 shows the course of a robot around an example area. 

 
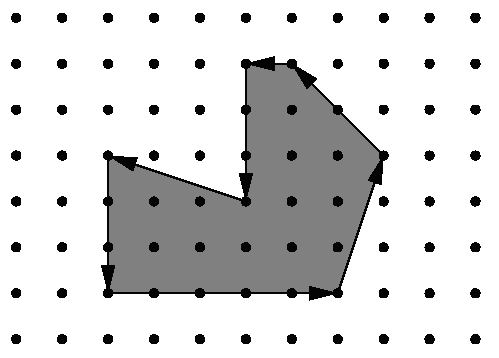
Figure 1: Example area. 

You are hired to write a program that calculates the area occupied by the new facility from the movements of a robot along its walls. You can assume that this area is a polygon with corners on a rectangular grid. However, your boss insists that you use a formula he is so proud to have found somewhere. The formula relates the number I of grid points inside the polygon, the number E of grid points on the edges, and the total area A of the polygon. Unfortunately, you have lost the sheet on which he had written down that simple formula for you, so your first task is to find the formula yourself. 

Input

The first line contains the number of scenarios. 
For each scenario, you are given the number m, 3 <= m < 100, of movements of the robot in the first line. The following m lines contain pairs 揹x dy�of integers, separated by a single blank, satisfying .-100 <= dx, dy <= 100 and (dx, dy) != (0, 0). Such a pair means that the robot moves on to a grid point dx units to the right and dy units upwards on the grid (with respect to the current position). You can assume that the curve along which the robot moves is closed and that it does not intersect or even touch itself except for the start and end points. The robot moves anti-clockwise around the building, so the area to be calculated lies to the left of the curve. It is known in advance that the whole polygon would fit into a square on the grid with a side length of 100 units. 

Output

The output for every scenario begins with a line containing 揝cenario #i:� where i is the number of the scenario starting at 1. Then print a single line containing I, E, and A, the area A rounded to one digit after the decimal point. Separate the three numbers by two single blanks. Terminate the output for the scenario with a blank line.

Sample Input

241 00 1-1 00 -175 01 3-2 2-1 00 -3-3 10 -3

Sample Output

Scenario #1:0 4 1.0Scenario #2:12 16 19.0

题意：

题目大意：以原点为起点然后每次增加一个x，y的值，求内部的点有多少个，在多边形边上的点有多少个，多边形的面积是多少。

分析：

1、以格子点为顶点的线段，覆盖的点的个数为GCD(dx,dy)，其中dx，dy分别为线段横向占的点数和纵向占的点数。

解释:当时很不理解这个公式为什么能算格点，后来动手画了一下图，才发现这个关系；

dx，dy互质时，组成的矩阵为互质小矩阵，格点为1。dx,dy有公约数n时，矩形可分割成相同的n^2份互质小矩阵，线段穿过的互质小矩阵为n份，故线段穿过的格点为n；（自己动手画一个6*3的矩阵研究一下）

2、Pick公式：s=a+b/2-1

平面上以格子点为顶点的简单多边形  面积=内部的点数+边上的点数/2-1。
3、任意一个多边形的面积等于按顺序求相邻两个点与原点组成的向量的叉积之和。

#include<cstdio>#include<cstring>#include<cmath>#include<algorithm>using namespace std;struct point{    int x,y;};int gcd(int m,int n){    if(!n)        return m;    return gcd(n,m%n);}int main(){    int t,m,cnt=1;    point A,B;    scanf("%d",&t);    while(t--)    {        int b=0;        float s=0;       A.x=0;A.y=0;       scanf("%d",&m);       for(int i=0;i<m;i++)       {           scanf("%d%d",&B.x,&B.y);           b+=gcd(abs(B.x),abs(B.y));           s+=B.x*A.y-B.y*A.x;           A.x+=B.x;A.y+=B.y;       }        s=abs(s);        printf("Scenario #%d:\n",cnt++);        printf("%d %d %.1f\n\n",(int)(s-b)/2+1,b,s/2);    }    return 0;}