平衡二叉树

平衡二叉树又称AVL树。它或者是颗空树，或者是具有下列性质的二叉树：它的左子树和右子树都是平衡二叉树，且左子树和右子树的深度之差的绝对值不超过1。若将二叉树节点的平衡因子BF定义为该节点的左子树的深度减去它的右子树的深度，则平衡二叉树上所有节点的平衡因子只可能为-1,0,1.只要二叉树上有一个节点的平衡因子的绝对值大于1，那么这颗平衡二叉树就失去了平衡。

假设我们已经有棵平衡二叉树，现在让我们来看看插入节点后，原来节点失去平衡后，我们进行选择的处理方式。

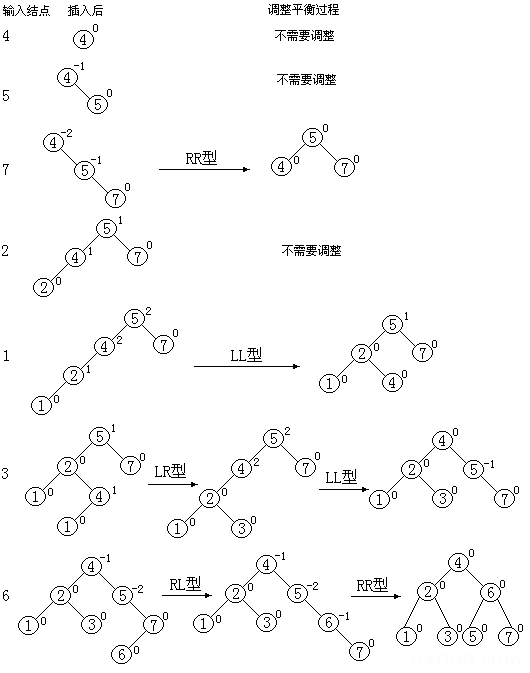
平衡二叉树多用于查找数据，所以平衡二叉树又是颗二叉排序树。

那么如何创建一颗平衡二叉树呢？

创建平衡二叉树，我们采用依次插入节点的方式进行。而平衡二叉树上插入节点采用递归的方式进行。递归算法如下：

（1）      若该树为一空树，那么插入一个数据元素为e的新节点作为平衡二叉树的根节点，树的高度增加1。

（2）      若待插入的数据元素e和平衡二叉树（BBST）的根节点的关键字相等，那么就不需要进行插入操作。

（3）      若待插入的元素e比平衡二叉树（BBST）的根节点的关键字小，而且在BBST的左子树中也不存在和e有相同关键字的节点，则将e插入在BBST的左子树上，并且当插入之后的左子树深度增加1时，分别就下列情况处理之。

(a)    BBST的根节点的平衡因子为-1（右子树的深度大于左子树的深度）：则将根节点的平衡因子更改为0，BBST的深度不变；

(b)    BBST的根节点的平衡因子为0（左右子树的深度相等）：则将根节点的平衡因子修改为1，BBST的深度增加1；

(c)    BBST的根节点的平衡因子为1（左子树的深度大于右子树的深度）：若BBST的左子树根节点的平衡因子为1，则需要进行单向右旋转平衡处理，并且在右旋处理后，将根节点和其右子树根节点的平衡因子更改为0，树的深度不变；

若BBST的左子树根节点的平衡因子为-1，则需进行先向左，后向右的双向旋转平衡处理，并且在旋转处理之后，修改根节点和其左，右子树根节点的平衡因子，树的深度不变；

（4）      若e的关键字大于BBST的根节点的关键字，而且在BBST的右子树中不存在和e有相同关键字的节点，则将e插入到BBST的右子树上，并且当插入之后的右子树深度加1时，分别就不同的情况处理之。

（a）      BBST的根节点的平衡因子是1（左子树的深度大于右子树的深度）：则将根节点的平衡因子修改为0，BBST的深度不变；

（b）      BBST的根节点的平衡因子是0（左右子树的深度相等）：则将根节点的平衡因子修改为-1，树的深度加1；

（c）      BBST的根节点的平衡因子为-1（右子树的深度大于左子树的深度）：若BBST的右子树根节点的平衡因子为1，则需要进行两次选择，第一次先向右旋转，再向左旋转处理，并且在旋转处理之后，修改根节点和其左，右子树根节点的平衡因子，树的深度不变；

若BBST的右子树根节点的平衡因子为1，则需要进行一次向左的旋转处理，并且在左旋之后，更新根节点和其左，右子树根节点的平衡因子，树的深度不变；

#include <stdio.h>#include <stdlib.h>/************************************************************************//*                    平衡二叉树---AVL                                  *//************************************************************************/#define LH +1#define EH  0#define RH -1typedef int ElemType;typedef struct BSTNode{ElemType data;int bf;//balance flagstruct BSTNode *lchild,*rchild;}*PBSTree;void R_Rotate(PBSTree* p){PBSTree lc = (*p)->lchild;(*p)->lchild = lc->rchild;lc->rchild = *p;*p = lc;}void L_Rotate(PBSTree* p){PBSTree rc = (*p)->rchild;(*p)->rchild = rc->lchild;rc->lchild = *p;*p = rc;}void LeftBalance(PBSTree* T){PBSTree lc,rd;lc = (*T)->lchild;switch (lc->bf){case LH:(*T)->bf = lc->bf = EH;R_Rotate(T);break;case RH:rd = lc->rchild;switch(rd->bf){case LH:(*T)->bf = RH;lc->bf = EH;break;case EH:(*T)->bf = lc->bf = EH;break;case RH:(*T)->bf = EH;lc->bf = LH;break;}rd->bf = EH;L_Rotate(&(*T)->lchild);R_Rotate(T);break;}}void RightBalance(PBSTree* T){PBSTree lc,rd;lc= (*T)->rchild;switch (lc->bf){case RH:(*T)->bf = lc->bf = EH;L_Rotate(T);break;case LH:rd = lc->lchild;switch(rd->bf){case LH:(*T)->bf = EH;lc->bf = RH;break;case EH:(*T)->bf = lc->bf = EH;break;case RH:(*T)->bf = EH;lc->bf = LH;break;}rd->bf = EH;R_Rotate(&(*T)->rchild);L_Rotate(T);break;}}int InsertAVL(PBSTree* T,ElemType e,bool* taller){if ((*T)==NULL){(*T)=(PBSTree)malloc(sizeof(BSTNode));(*T)->bf = EH;(*T)->data = e;(*T)->lchild = NULL;(*T)->rchild = NULL;}else if (e == (*T)->data){*taller = false;return 0;}else if (e < (*T)->data){if(!InsertAVL(&(*T)->lchild,e,taller))return 0;if(*taller){switch ((*T)->bf){case LH:LeftBalance(T);*taller = false;break;case  EH:(*T)->bf = LH;*taller = true;break;case RH:(*T)->bf = EH;*taller = false;break;}}}else{if(!InsertAVL(&(*T)->rchild,e,taller))return 0;if (*taller){switch ((*T)->bf){case LH:(*T)->bf = EH;*taller = false;break;case EH:(*T)->bf = RH;*taller = true;break;case  RH:RightBalance(T);*taller = false;break;}}}return 1;}bool FindNode(PBSTree root,ElemType e,PBSTree* pos){PBSTree pt = root;(*pos) = NULL;while(pt){if (pt->data == e){//找到节点，pos指向该节点并返回true(*pos) = pt;return true;}else if (pt->data>e){pt = pt->lchild;}elsept = pt->rchild;}return false;}void InorderTra(PBSTree root){if(root->lchild)InorderTra(root->lchild);printf("%d ",root->data);if(root->rchild)InorderTra(root->rchild);}int main(){int i,nArr[] = {1,23,45,34,98,9,4,35,23};PBSTree root=NULL,pos;bool taller;for (i=0;i<9;i++){InsertAVL(&root,nArr[i],&taller);}InorderTra(root);if(FindNode(root,103,&pos))printf("\n%d\n",pos->data);elseprintf("\nNot find this Node\n");return 0;}