HDU4651|HDU1028 Partition 整数拆分公式法

题目链接：HDU4651

题目大意：给你n,求出n的拆分数，例如p(4)=5  4=1+1+1+1 ，4=1+1+2 ， 4=1+3， 4=2+2，4=4；五种拆分，无序。

知识点：

1、广义五边形数：广义五边形数

广义五边形数的公式和五边形数相同，只是n可以为负数和零，n 依序为0, 1, -1, 2, -2, 3, -3, 4...，广义五边形数也可以用下式表示：

{\displaystyle p_{n}={\frac {3n^{2}\pm n}{2}}}

n 依序为0, 1, 2, 3, 4...，

其产生的数列如下：

0, 1, 2, 5, 7, 12, 15, 22, 26, 35, 40, 51, 57, 70, 77, 92, 100, 117, 126, 145, 155, 176, 187, 210, 222, 247, 260, 287, 301, 330, 345, 376, 392, 425, 442, 477, 495, 532, 551, 590, 610, 651, 672, 715, 737, 782, 805, 852, 876, 925, 950, 1001, 1027, 1080, 1107, 1162, 1190, 1247, 1276, 1335... (OEIS:A001318)

在欧拉的整数分拆理论中，五边形数定理说明广义五边形数和整数分拆的关系。

用第n个五边形数（n>2）排列组成的正五边形，外围点的个数有{\displaystyle 5(n-1)}个，因此在内部的点个数为：

{\displaystyle {\frac {3n^{2}-n}{2}}-5(n-1)={\frac {3n^{2}-11n+10}{2}}={\frac {(3n-5)(n-2)}{2}}={\frac {3(n-2)^{2}+(n-2)}{2}}}

刚好也是一个广义五边形数。

所有的整数都可以表示成不超过3个广义五边形数的和^[1]。

若三角形数可以被3整除，则除以3之后的数必为广义五边形数^[2]。

2、

整数拆分的公式

的生成函数是

{\displaystyle \sum _{n=0}^{\infty }p(n)x^{n}=\prod _{k=1}^{\infty }\left({\frac {1}{1-x^{k}}}\right)}

当|x|<1，右边可写成：

{\displaystyle (1+x+x^{2}+x^{3}+...)(1+x^{2}+x^{4}+x^{6}+...)(1+x^{3}+x^{6}+...)...}

{\displaystyle p(n)}生成函数的倒数为欧拉函数，利用五边形数定理可得到以下的展开式：

{\displaystyle \prod _{k=1}^{\infty }(1-x^{k})=\sum _{i=-\infty }^{\infty }(-1)^{i}x^{i(3i-1)/2}.}

将{\displaystyle p(n)}生成函数配合五边形数定理，可以得到以下的递归关系式

{\displaystyle p(n)=\sum _{i}(-1)^{i-1}p(n-q_{i})}

其中{\displaystyle q_{i}}是第{\displaystyle i}个广义五边形数。

3、就是利用最后一个公式来做题。注意的是qi是两个部分，最后一个公式也可以写成

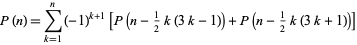
然后根据这个公式把样例手算一下 ，就很清晰了。

AC代码

/*整数拆分 公式法 打表2017年8月3日00:15:14AC代码*/ #include<stdio.h>#include<iostream>#include<string.h>using namespace std;typedef long long ll;const int mod=1e9+7;const int maxn=1e5+10; ll ans[maxn];int t,n;void init(){memset(ans,0,sizeof(ans));ans[0]=1;for(int i=1;i<=maxn;i++){int f;//代表这一位是加还是捡 for(int j=1;;j++){int a,b;/*i减去对应的两个广义五边形数*/ a=i-j*(3*j-1)/2;b=i-j*(3*j+1)/2;/*根据i判定这一位的正负*/if(j&1) f=1;//奇数 加 else f=-1;//偶数 减/*坑点，如果两个p(n-qi)都小于零，那么就加到这里为止*/ if(a<0&&b<0) break;/*任何一个p(n-qi)大于零都要算进去*/if(a>=0) ans[i]=(ans[i]+f*ans[a]) %mod;if(b>=0) ans[i]=(ans[i]+f*ans[b]) %mod;}ans[i]=(ans[i]+mod)%mod;}}int main(){cin.sync_with_stdio(false);cin>>t;init(); while(t--){cin>>n;cout<<ans[n]<<endl;}return 0;}

再来一个同类型的题目HDU1028

与上面不同的是，不需要模直接输出即可，AC代码

/*2017年8月16日10:07:18HDU1028AC */#include<stdio.h>  #include<iostream>  #include<string.h>  using namespace std;  typedef long long ll;    //const int mod=1e9+7;  const int maxn=1e5+10;   ll ans[maxn];  int t,n;  void init(){      memset(ans,0,sizeof(ans));      ans[0]=1;            for(int i=1;i<=maxn;i++){          int f;//代表这一位是加还是捡           for(int j=1;;j++){              int a,b;              /*i减去对应的两个广义五边形数*/               a=i-j*(3*j-1)/2;              b=i-j*(3*j+1)/2;              /*根据i判定这一位的正负*/              if(j&1) f=1;//奇数 加               else    f=-1;//偶数 减              /*坑点，如果两个p(n-qi)都小于零，那么就加到这里为止*/               if(a<0&&b<0) break;              /*任何一个p(n-qi)大于零都要算进去*/              if(a>=0) ans[i]=(ans[i]+f*ans[a]) ;              if(b>=0) ans[i]=(ans[i]+f*ans[b]) ;          }          //ans[i]=(ans[i]+mod)%mod;      }        }    int main(){      cin.sync_with_stdio(false);     // cin>>t;      init();       while(cin>>n){                   cout<<ans[n]<<endl;      }      return 0;  }