Partition(hdu4651)2013 Multi-University Training Contest 5----(整数拆分一)
来源:互联网 发布:linux libxml2 安装 编辑:程序博客网 时间:2024/05/16 16:58
Partition
Time Limit: 6000/3000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 954 Accepted Submission(s): 545
Problem Description
How many ways can the numbers 1 to 15 be added together to make 15? The technical term for what you are asking is the "number of partition" which is often called P(n). A partition of n is a collection of positive integers (not necessarily distinct) whose sum equals n.
Now, I will give you a number n, and please tell me P(n) mod 1000000007.
Now, I will give you a number n, and please tell me P(n) mod 1000000007.
Input
The first line contains a number T(1 ≤ T ≤ 100), which is the number of the case number. The next T lines, each line contains a number n(1 ≤ n ≤ 105) you need to consider.
Output
For each n, output P(n) in a single line.
Sample Input
45111519
Sample Output
756176490
Source
2013 Multi-University Training Contest 5
题意:问一个数n能被拆分成多少种方法
首先你要知道母函数+然后你要知道五边形数定理;
设第n个五边形数为

对应图形如下:
设五边形数的生成函数为
以上是五边形数的情况。下面是关于五边形数定理的内容:
五边形数定理是一个由欧拉发现的数学定理,描述欧拉函数展开式的特性。欧拉函数的展开式如下:
欧拉函数展开后,有些次方项被消去,只留下次方项为1, 2, 5, 7, 12, ...的项次,留下来的次方恰为广义五边形数。
五边形数和分割函数的关系
欧拉函数的倒数是分割函数的母函数,亦即:


上式配合五边形数定理,有:
在 n>0 时,等式右侧的系数均为0,比较等式二侧的系数,可得
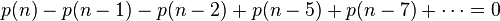
因此可得到分割函数p(n)的递归式:
例如n=10时,有: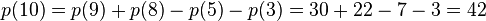
所以,通过上面递归式,我们可以很快速地计算n的整数划分方案数p(n)了。
详见维基百科:https://zh.wikipedia.org/wiki/%E4%BA%94%E8%A7%92%E6%95%B0#.E5.BB.A3.E7.BE.A9.E4.BA.94.E9.82.8A.E5.BD.A2.E6.95.B8 或 https://zh.wikipedia.org/wiki/%E4%BA%94%E9%82%8A%E5%BD%A2%E6%95%B8%E5%AE%9A%E7%90%86
转载请注明出处:http://blog.csdn.net/u010579068
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=4651
详见代码:
#include<iostream>#include<cstdio>#define NN 100005#define LL __int64#define mod 1000000007using namespace std;LL wu[NN],pa[NN];void init(){ pa[0]=1; pa[1]=1; pa[2]=2; pa[3]=3; LL ca=0; for(LL i=1;i<=100000/2;i++) { wu[ca++]=i*(3*i-1)/2; wu[ca++]=i*(3*i+1)/2; if(wu[ca-1]>100000) break; } for(LL i=4;i<=100000;i++) { pa[i]=(pa[i-1]+pa[i-2])%mod; ca=1; while(wu[2*ca]<=i) { if(ca&1) { pa[i]=(pa[i]-pa[i-wu[2*ca]])%mod; pa[i]=(pa[i]%mod+mod)%mod; if(wu[2*ca+1]<=i) pa[i]=(pa[i]-pa[i-wu[2*ca+1]])%mod; pa[i]=(pa[i]%mod+mod)%mod; } else { pa[i]=(pa[i]+pa[i-wu[2*ca]])%mod; pa[i]=(pa[i]%mod+mod)%mod; if(wu[2*ca+1]<=i) pa[i]=(pa[i]+pa[i-wu[2*ca+1]])%mod; pa[i]=(pa[i]%mod+mod)%mod; } ca++; } }}int main(){ int T,n; init(); scanf("%d",&T); while(T--) { scanf("%d",&n); printf("%I64d\n",pa[n]); } return 0;} 0 0
- Partition(hdu4651)2013 Multi-University Training Contest 5----(整数拆分一)
- Integer Partition(hdu4658)2013 Multi-University Training Contest 6 整数拆分二
- 2013 Multi-University Training Contest 5
- hdu 4638 Group(2013 Multi-University Training Contest 4)
- hdu 4911 Inversion ( 2014 Multi-University Training Contest 5)
- hdu 5791 2016 Multi-University Training Contest 5(dp)
- 2016 Multi-University Training Contest 5 1011 Two(DP)
- HDU4651|HDU1028 Partition 整数拆分公式法
- 2013 Multi-University Training Contest 1
- 2013 Multi-University Training Contest 1
- 2013 Multi-University Training Contest 2
- 2013 Multi-University Training Contest 1
- 2013 Multi-University Training Contest 1
- 2013 Multi-University Training Contest 3
- 2013 Multi-University Training Contest 3
- 2013 Multi-University Training Contest 4
- 2013 Multi-University Training Contest 6
- 2013 Multi-University Training Contest 7
- 由现实世界到抽象世界
- html5开发之viewport使用 移动前端开发之viewport的深入理解
- Struts获取HttpServletRequest / HttpSession / ServletContext / HttpServletResponse对象
- 使tableview每个section显示不同行数的方法
- oc三种传值方式:通知传值,代理传值,block传值
- Partition(hdu4651)2013 Multi-University Training Contest 5----(整数拆分一)
- 调度时机分析之被动调度(之中断处理返回)
- IOS--Delegate 自定义之个人感悟
- noi2015模板-决策单调性
- Linux 设备驱动之 DTS 描述的资源
- JS的面向对象的基础
- VC运行库依赖导致的InnoSetup安装程序调用DLL报错:无法导入DLL
- srm 540
- 1.3 编程范式







