HDU 5528 Count a*b ACM/ICPC 2015 Changchun（数论）

Count a * b

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 262144/262144 K (Java/Others)
Total Submission(s): 811    Accepted Submission(s): 299

Problem Description

Marry likes to count the number of ways to choose two non-negative integersa and b less than m to make a×b mod m≠0.
Let's denote f(m) as the number of ways to choose two non-negative integers a and b less than m to make a×b mod m≠0.
She has calculated a lot of f(m) for different m, and now she is interested in another function g(n)=∑m|nf(m). For example, g(6)=f(1)+f(2)+f(3)+f(6)=0+1+4+21=26. She needs you to double check the answer.

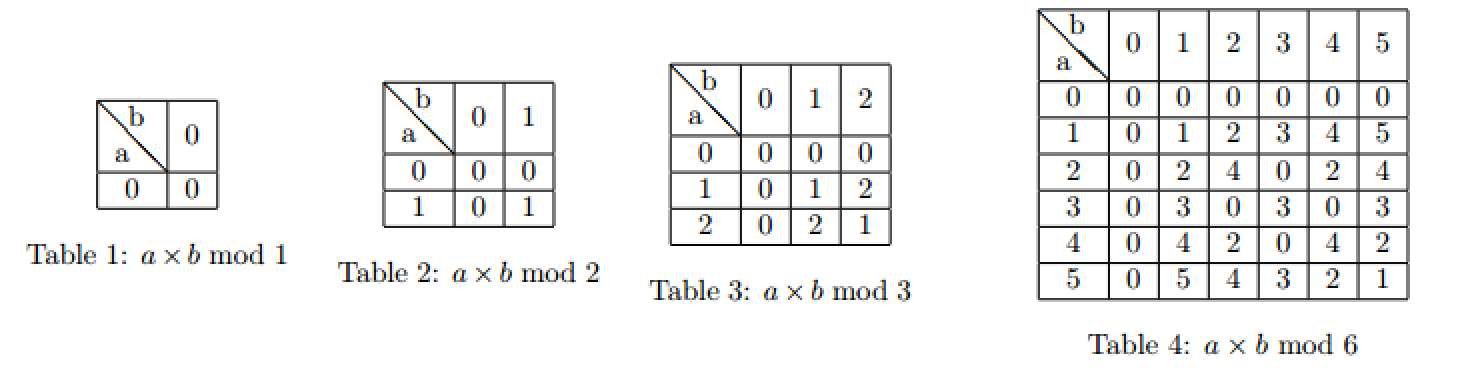
Give you n. Your task is to find g(n) modulo 264.

Input

The first line contains an integer T indicating the total number of test cases. Each test case is a line with a positive integern.
1≤T≤20000
1≤n≤109

Output

For each test case, print one integer s, representing g(n) modulo 264.

Sample Input

26514

Sample Output

26328194

Source

2015ACM/ICPC亚洲区长春站-重现赛（感谢东北师大）

        非常棒的一道数论题，而且还是一道金牌题，A了几乎就是金牌……

        至于具体推到姿势，由于符号难写，我就用某个大神的手迹来说明吧，大神写的真的很好。原文地址：http://blog.csdn.net/firstlucker/article/details/49336427

                          

         下面，我解释一下画横线那一步。之前已经是求到了sigma(gcd(a,x))，相当于1~x中所有数字与x的gcd之和。BTW，关于这个可以再说一篇文章，POJ 2480就是只求这个东西，这个利用积性可以巧妙的解决，具体可以看下一篇文章。在这里我们可以考虑x的每个约数作为gcd的次数，然后计算求和。于是我们就可以按照画横线那一步那样，枚举x的约数d，然后对于每一个d统计有多少个合法的。而所谓合法就是两个数字除以这个约数之后的gcd为1。a是从1~x取的，如果a不是d的倍数显然可以忽略，于是我们可以继续往下化简，得到横下往下那一步，用i代替a/d。此时i的取值是1~x/d，那么这个判定条件就变成了1~x/d中有多少个数字与x/d的gcd为1，或者说互质。那么很顺其自然的就可用欧拉函数写出最后的式子。

        但是即使推到了这一步我们还是不能在规定时间内解出答案，因为很多组数据，而且n可以取1e9，也不可能预处理出那么多的phi。于是我们还得继续化简。

  

        接着解释这个。首先是第一个画横线那里，说实话，我第一次看到的时候真的是一脸懵逼。然后后来慢慢回想起来，这是一个关于整数合式的一个定理，在《具体数学》书中也出现过。具体来说是这样子的：

                   

        知道了这个转换之后，我们就可以继续说事了。然后看第二条横线那，这个又是如何转换过来的呢？上面一行想到与是n/d所有约数的欧拉函数之和，下面画横线那变成了n/d。其实这是一个定理，一个数字x的所有约数的欧拉函数之后等于它本身。这样我们就可以顺其自然的化简到最后一行了，其中最后一行中h(n)表示n的约数个数。知道此时，我们算是比较完美的解决了后面那一部分的东西，但是前半部分东西还是不太好，约数的平方和，如果一个约数一个的算还是会TLE，前面努力就白费了，于是还要继续找性质化简。

        接下来，我们想到了积性。可以证明一个数字的约数平方和是一个积性函数，不仅如此，一个数约数的k次方和都是积性函数。所以我们可以得出最终式子：

                    

        然后具体细节的话还要注意，本题常数卡的比较厉害，需要预处理出素数表。然后在运算过程中虽然说对2^64取模（用unsigned long long即可），但是还是要做一些防止溢出的处理，因为有些东西本来不会溢出的，但是中间溢出的话会导致WA。具体见代码，还是非常刺激的一道题：

#include<bits/stdc++.h>#define ULL unsigned long long#define N 101000using namespace std;int prime[N],tot,n,m,t;bool isprime[N];void getlist(int listsize)//欧拉筛预处理出素数表{    memset(isprime,1,sizeof(isprime));    isprime[1]=false; tot=0;    for(int i=2;i<listsize;i++)    {        if(isprime[i]) prime[++tot]=i;         for(int j=1;j<=tot&&i*prime[j]<listsize;j++)         {            isprime[i*prime[j]]=false;            if(i%prime[j]==0)break;        }    }}int main(){    getlist(N);    int T_T; cin>>T_T;    while(T_T--)    {        scanf("%d",&n);        ULL x=1,y=n,p;        for(int i=1;prime[i]*prime[i]<=n;i++)        {            if (n%prime[i]==0)            {                t=1; p=1;                while(n%prime[i]==0)                    t++,n/=prime[i],p*=prime[i];                p*=prime[i]; y*=t;                ULL a=(p-1)/(prime[i]-1),b=p+1,c=prime[i]+1;                x*=((a/c)*(b/c)*c+a%c*(b/c)+b%c*(a/c));//防止溢出操作            }        }        if (n>1) x*=((ULL)n*n+1),y*=2;        printf("%I64u\n",x-y);    }    return 0;}