可视化信息论（译）

我喜欢开拓新思路的去思考世界的感觉。尤其喜欢一些模糊的概念从抽象变成具体的概念。信息论就是这样的一个例子。
信息论给了我们精确的语言去描述许多事情：我有多不确定？所了解到的关于问题A的答案能告诉我多少问题B的答案？一套信念和另一套有多么相似？从孩童时代起，我就有这些非正式的想法，但是信息论使得它们成为了精确的、有力的理念。这些想法有多种多样的应用：从数据压缩到量子物理，再到机器学习，以及前述应用之间广阔的领域。
不幸的是，信息论看起来有点吓人。我不觉得它应该是这样的。事实上，许多核心概念都完全可以可视化解释！

可视化概率分布

---

在我们进入信息论的大门之前，让我们想一想我们能够把概率分布想象得有多简单？稍后我们将会需要这个，而且现在去提出是很方便的。作为一个额外提示，这些可视化概率的技巧在它们自己中是十分有用的！
我生活在加利福利亚。这里偶尔下雨，但更多时候是晴天！我们假设75%的时间是晴天。很容易得到下图：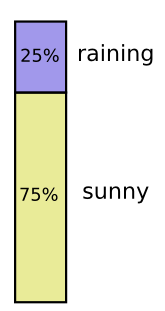

大多数时候，我穿着短袖，但是有时候我也穿外套。假设我有38%的时间穿外套。容易得到下图：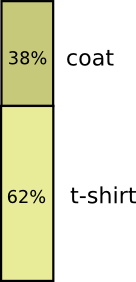

如果我想把这两张图同时可视化我应该怎么办呢？如果它们不相互影响的话这是很简单的——如果它们是独立的。举例来说，今天我是否穿着短袖或者雨衣并不影响下周的天气。我们可以使用一个轴作为一个变量另一个轴作为另一个变量来画出下图：

注意到垂直的和水平的线一路通过。这就是独立所看起来的样子！我穿着雨衣并不会改变在一周之内将会下雨这样的事实。换句话说，我穿着雨衣和下周将会下雨的概率仅仅是我穿着雨衣的概率乘以将会下雨的概率。它们并不会相互影响。
当变量相互影响的时候，会出现一些额外的详细的变量对的概率同时还会遗失其他一些概率。这些额外的概率是我穿着雨衣并且下雨因为这些变量是相关的，它们使得互相更可能。我在下雨天穿着雨衣就比我穿着雨衣但是另外一些天下雨的概率要大。
从视觉上来说，这看起来就像是一些方块由于额外的概率膨胀，同时其他一些方块由于不太可能的事件搭配而缩小：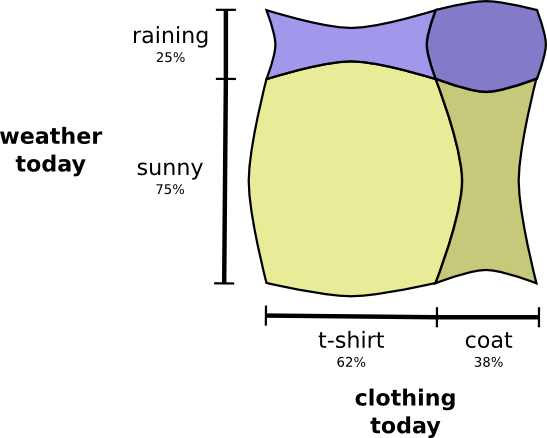

但是尽管这个看起来比较酷，这对与理解发生了什么却并没有太大的用处。
相反，我们先来看看天气这一个变量。我们知道晴天或下雨的可能性。在两种情况下，我们可以看看条件概率。如果是晴天我有多大可能穿着短袖？如果是雨天我有多大可能穿着雨衣？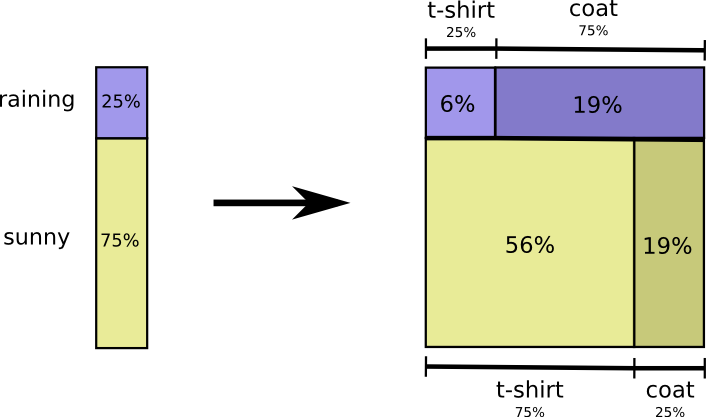

有25%的可能性会下雨。如果下雨了，有75%的可能性我会穿雨衣。因此，下雨并且我穿雨衣的概率是25%乘以75%也即是19%。下雨并且我穿雨衣的概率是下雨的概率乘以如果下雨那么我穿雨衣的概率。我们写作：

这是概率论中最基础的例子之一：

我们来展开这个分布，把它展开成两部分。首先我们来看看一个变量的概率比如天气将会取得一个确定的值。然后我们看看另一个变量的概率，在本例中是衣服，它将会取一个基于第一个变量的确定的值。
选择哪一个变量作为第一个变量是随机的。我们也可以很容易地以衣服开始，然后观察基于衣服的天气的概率。这也许感觉不太直观，因为我们认为衣服和天气有因果关系而不是其它关系……但这个仍然起作用！
让我们来仔细看看一个例子。如果我们随便选择一个日子，那么就有38%的概率我会穿雨衣。如果我们知道我穿雨衣，那么有多大可能下雨？当然，我在雨天穿雨衣比晴天穿雨衣的可能性要大，但是雨水在加利福利亚比较少，因此得出了有50%的机会会下雨。并且下雨并且我穿着雨衣的概率是我穿着雨衣的概率乘以如果我穿着雨衣下雨的概率也即大概是19%：

这给了我们第二种方式来可视化相同的概率分布。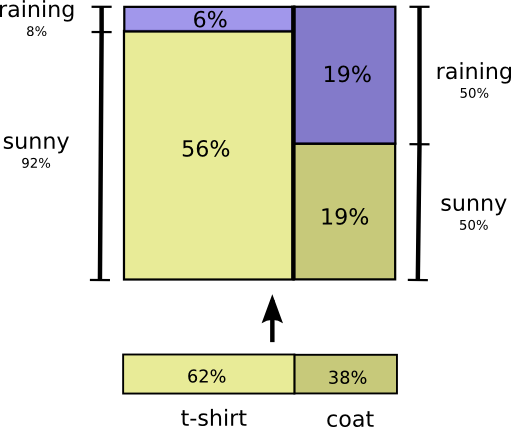

需要指出的是标签比之前的图标有些稍微不同的含义：短袖和雨衣现在被称之为边缘分布，也即是在不考虑天气的情况下我穿着各种衣服的概率。在另一方面，现在有两套下雨和晴天的标签，因为它们是分别基于我穿着短袖和我穿着雨衣的概率。
（你可能听说过贝叶斯原理。如果你愿意，你可以把上述看做是在两种不同的概率分布的转换！）

补充：辛普森悖论

---

这些技巧对于可视化概率分布有帮助吗？我认为是有的！在稍后我们可视化信息论之前将会有用，因此我希望先说一些离题的并且使用它们去探索辛普森悖论。辛普森悖论是一个十分不直观的统计学现象。它很难以一种直观的方式去理解。Michael Nielsen写了一篇不错的文章，Reinventing Explanation,这篇文章用不同的方式去解释它。我喜欢使用我们在之前章节所叙述的技巧自己去解决。
两种治疗肾结石的手段被测试。一半的病人得到了A治疗同时另一半得到了B治疗。接受到B治疗的病人比接受到A治疗的病人更可能存活。

然而，仅仅患有小块肾结石的病人如果接受A治疗更可能存活。同时患有大块肾结石的病人如果接受A治疗也更可能存活！这怎么可能？
这个问题的核心是研究并没有随机。接受A治疗的患者更可能患有大块肾结石，同时接受B治疗的患者更可能患有小块肾结石。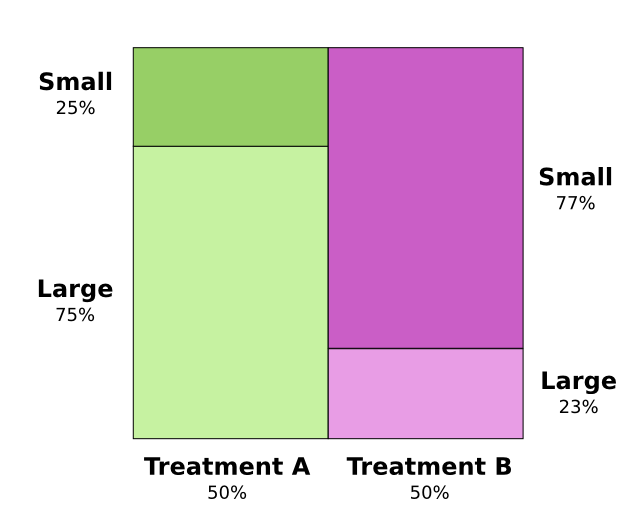

正如上图所指出的那样，患有小块肾结石的病人通常来说更可能存活。
为了更好地理解这个，我们可以结合前两个图表，生成了一个标出大块肾结石和小块肾结石的存活率的3维的图表。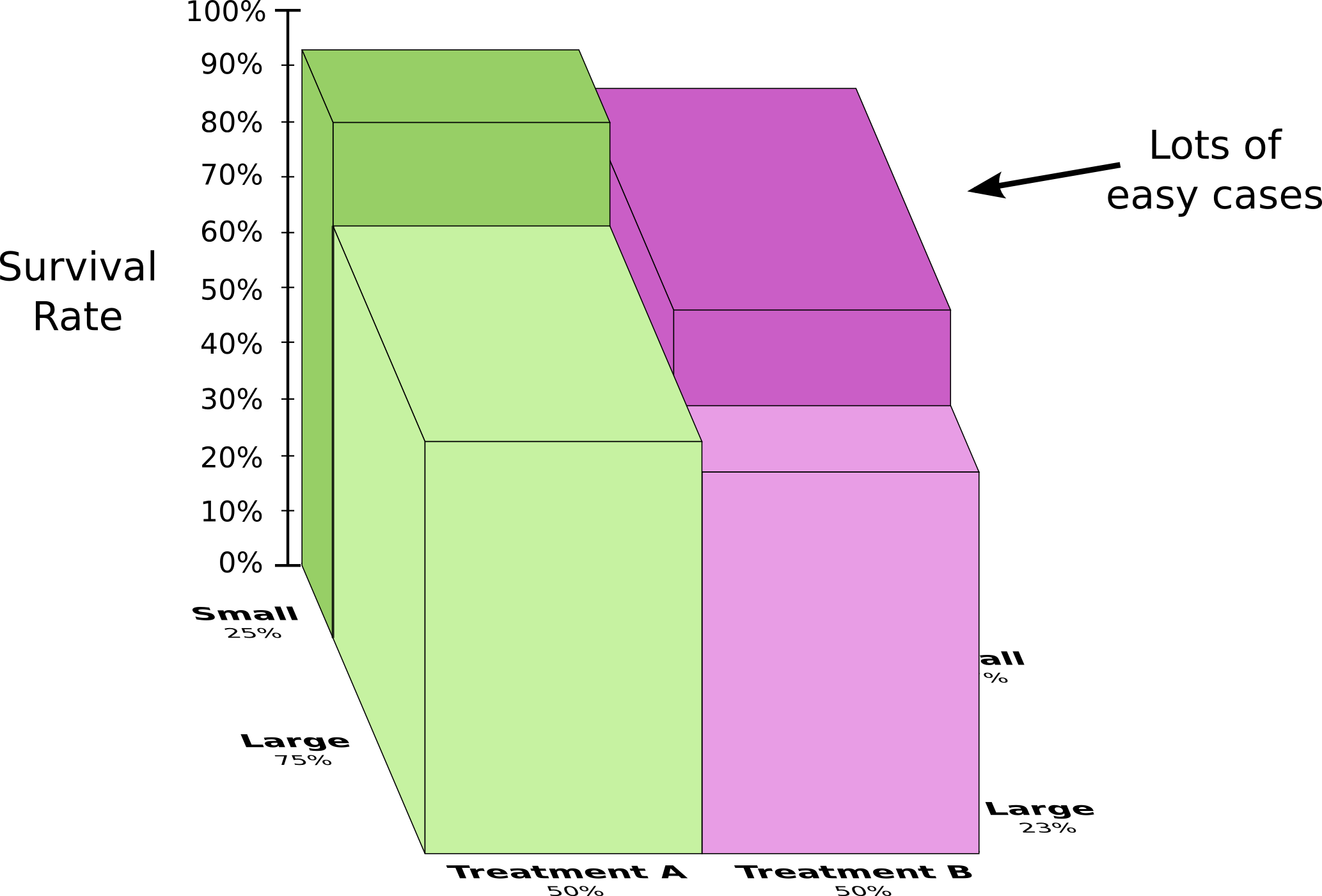

现在我们可以看到在小块的病情和大块的病情下，A治疗打败了B治疗。B治疗看起来更好仅仅是因为实施B治疗的病人更可能存活在小块的场景下。

代码

---

既然我们有可视化可能性的方法，我们就可以深入信息论了。
我们先假定我有一个朋友Bob。Bob很喜欢动物。他一直在谈论动物。事实上，他一直只说四个单词：dog、cat、fish、bird。
几周前，尽管是我想象出来的，Bob前往澳大利亚。而且，他决定他只想用二进制交流。所有我从Bob处得到的信息都是类似这样的：

为了交流，Bob和我建立了一套准则，也就是把单词映射到位序列的方法。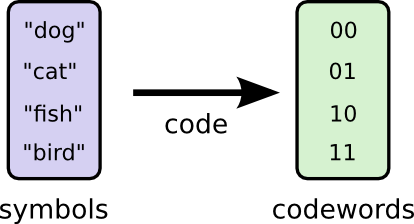

为了发送消息，Bob把每一个字符都替换成了相关的代码，然后把它们拼接在一起形成了编码字符串。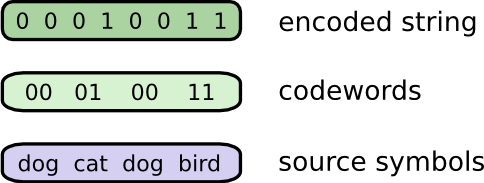

可变长度的代码

---

不幸的是，交流服务在假想-澳大利亚之间是很昂贵的。我必须为我从Bob处收到的消息的每一位付出5美元的代价。我有提到Bob喜欢说很多吗？为了防止我破产，Bob和我决定我们应该调查是否有其他方式我们能够使我们的平均信息长度更短。
正如上面指出，Bob并不是说所有单词一样频繁。Bob真的很喜欢dog。他总是在说dog。有时，他会说其他动物——尤其是他的狗喜欢追逐的cat——但是大多数时候他谈论dog。这有一幅他的单词频率图：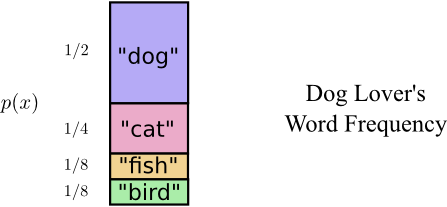

这看起来是很有希望的。我们旧的编码长度为2，不管它们多么常用。
这有一个很不错的方式去可视化这个。在下面这张图表中，我们使用竖直的轴去可视化每一个单词的概率，%P(x)%,并且使用水平的轴去可视化相关的代码的长度，L(x)。注意到这个区域是我们发送的代码的平均长度——在这个例子中是2位。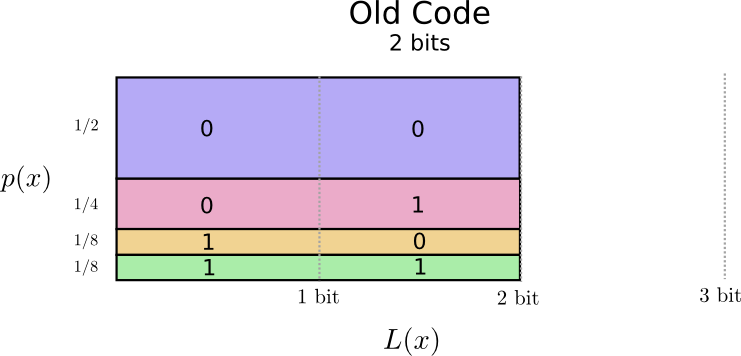

也许我们可以变聪明并且制造出可变长度的代码，在这套代码中常用的单词会特别短。遇到的挑战是代码词之间的竞争——让一些更短就会使得另一些更长。为了最小化信息长度，我们希望所有的代码词都很短，但是我们尤其希望经常被使用的会很短。因此得出的代码对于常用的单词（比如：dog）有更短的代码词，对于不太常用的代码词（比如：bird）使用更长的代码词。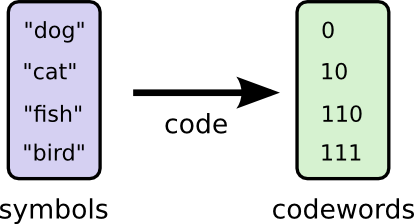

让我们再次可视化这些代码。注意到最常用的代码词更短，同时不太常用的变得更长。净计算的结果是更小的区域。这符合期望的更小的代码长度。平均来说，代码的长度现在是1.75位！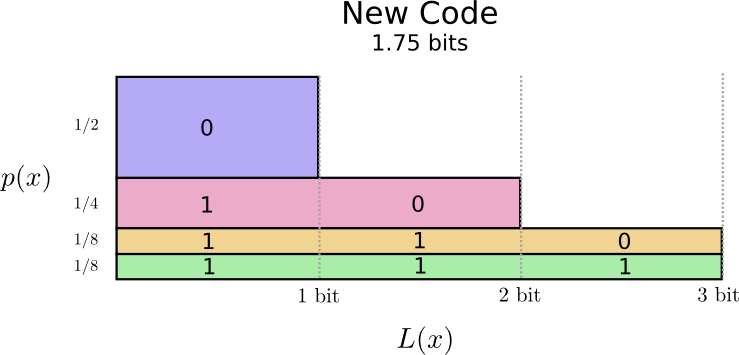

（你也许想要知道：为什么不使用1本身作为一个代码词？遗憾的是当我们对编码字符串解码时这将会造成模棱两可的境况。我们将会简短的谈论这些）
事实证明这种代码时最可能的代码。对于这种分布，没有任何其他的代码能够给出平均长度小于1.75位的代码。
这仅仅是一个基本的限制。交流哪些单词被说出了和这种分布会出现什么事件要求我们平均长度至少1.75位。无论我们的代码多么聪明，这都是不可能的去得到更少的代码长度。我们称这个基本限制为分布熵——我们将会讨论更多细节。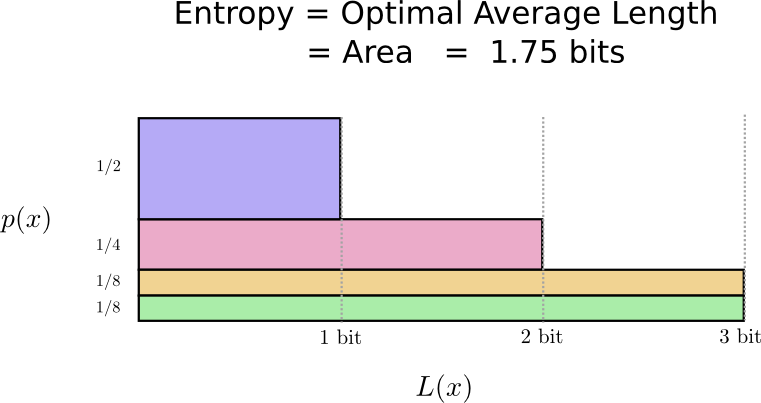

如果我们想要理解这个限制，关键是理解在让一些代码更短和让另一些代码更长之间做权衡。一旦我们理解了这个，我们就能够理解最好的代码是什么。

代码空间

---

有两个代码长度为1位：0和1.有四个代码长度为2位：00,01,10,11。每加一位就会使得代码的数量加倍。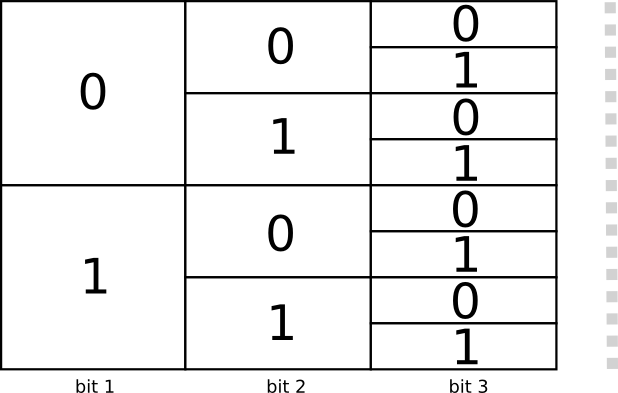

我们感兴趣的是可变长度的代码，也就是说一些代码的长度比另一些要长。一种可能的简单情况是我们有8个长度为3位的代码词。还有可能有更复杂的情况，比如两个代码词的长度是2,四个代码词的长度是3.是什么决定了我们能有多少不同长度的代码词？
回忆一下Bob把它的信息通过用代码词替换每一个单词并且拼接它们来转换成了编码字符串。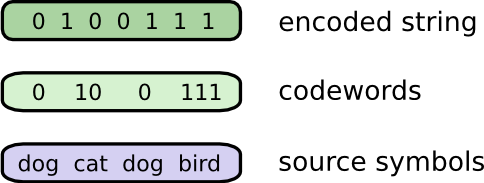

在制作可变长度的代码时，有一个很精细的问题我们需要注意。我们怎样把编码字符串划分成代码词？当所有的代码词都是相同长度的时候这很容易——仅仅把字符串划分成几组就行了。但是当不同长度的代码词出现时，我们确实需要注意到这个内容。
我们希望我们的代码是能有独一无二的解码方法的，仅仅有一种解码编码字符串的方法。我们不希望这是含糊不清的。如果我们有一些特殊的结束字符，这将会很容易。但是我们没有——我们仅仅发送0和1.我们需要去寻找一个拼接代码词的序列并且能够指出在哪里停止。
使得代码不能被唯一的解码是容易的。举个例子，想象0和01都是代码词。编码字符串0100111的第一个代码词是什么将会是不清楚的——这应该是清楚的！
我们希望是如果我们能看到一个特殊的代码词，就不应该有更长的代码词也包含这个。另一个达到这个目的的方法是所有代码词都不应该成为其他代码词的前缀。这称之为前缀性质，遵循这个性质的代码称之为前缀码。
一种有用的方式是每一个代码词都会有一个可能的代码词空间的牺牲。如果我们采用代码词10，我们就会失去任何以10为前缀的代码词的可能。我们不能使用010或者011010110因为这样会含糊不清——我们在失去它们。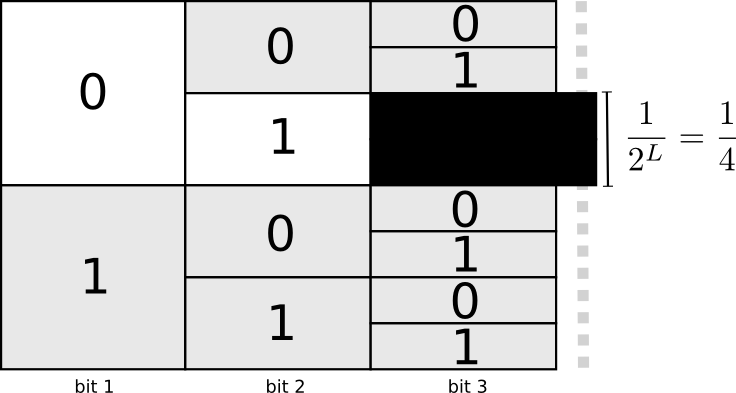

因为四分之一的代码词都是以01开头，我们就牺牲了四分之一的可能的代码词。
这是我们为有一个仅仅2位长的代码词而付出的代价！这个牺牲还意味着所有其他的代码词都会更长一位。总会存在在不同的代码词之间的权衡。短的代码词要求你要牺牲更多的可能代码词的空间，阻住了其他代码词更短。我们需要搞清楚的是正确的权衡是什么！

最佳编码

---

你可以把这当做在得到短的代码词的过程中存在有限的预算。我们为一个代码词牺牲了一部分可能的代码词。
获得一个长度为0的代码词的代价是1，所有可能的代码词——如果你想有一个长度为0的代码词，那么你就不能有其他任何代码词。长度为1的代码词比如说‘0’的代价是1/2因为一半的可能的代码词都是以0开头的。长度为2的代码词比如说‘01’的代价是1/4因为四分之一的可能的代码词都是以01开头。通常来说，代码词的代价随着代码词的长度指数递减。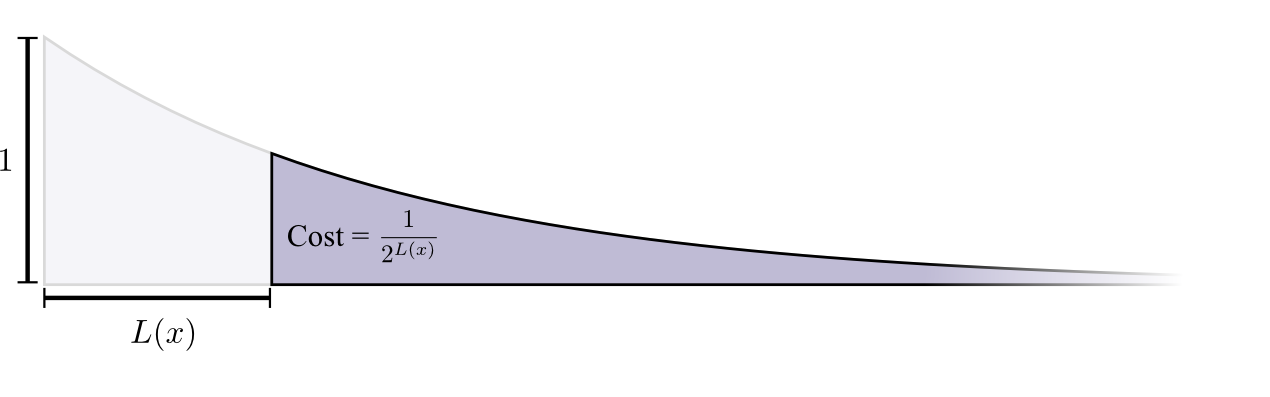

需要指出的是如果成本指数减少，那么高度和面积都是这样的！
我们想要短的代码词因为我们短的平均信息长度。每一个代码词都使得平均信息长度更长通过它的概率乘以它的长度。举个例子，如果我们想要发送一个长度为4位概率为50%的代码词，我们的平均信息长度就会在增加2位。我们可以画成一个矩形：

这两个值是相关的。我们付出的代价决定了代码词的长度。代码词的长度控制了它增加了多少平均信息长度。我们可以把这两个画在一起：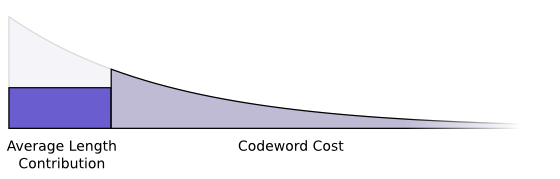

短的代码词减少平均信息长度但是很昂贵，同时长的代码词增加平均代码长度但是很便宜：

使用我们有限预算的最佳用法是什么呢？对于每一个事项我们应该花费多少在代码词上呢？
就像是一个人想要去更多地投资在人们经常使用的工具上，我们想要花费更多在在人们使用频繁的代码词上。这有一个特别自然的方法：把我们的预算按照它们常用的比例来分配。因此，如果一个事50%的时间都在发生，我们就花费50%的预算为它获得一个短的代码词。但是如果一个事只在1%的时间发生，我们就仅仅花费1%的预算，因为我们不太关心这个代码词是否长。
这是十分自然的，但是这是最优化的方式吗？是的，我将证明它！
接下来的证明是可视化的而且应该是容易理解的，但是将会经历本文最难的部分。读者可以把这个作为一个已知随意跳过，调到下一部分。
让我们来画一个具体的例子，我们需要交流两个可能受到事情哪个会发生。事件a以概率p(a)发生，事件b以概率p(b)发生。我们把我们的预算按照上文所描述的自然的方式来分配，为a花掉我们预算的p(a)部分，为b花掉我们预算的p(b)部分。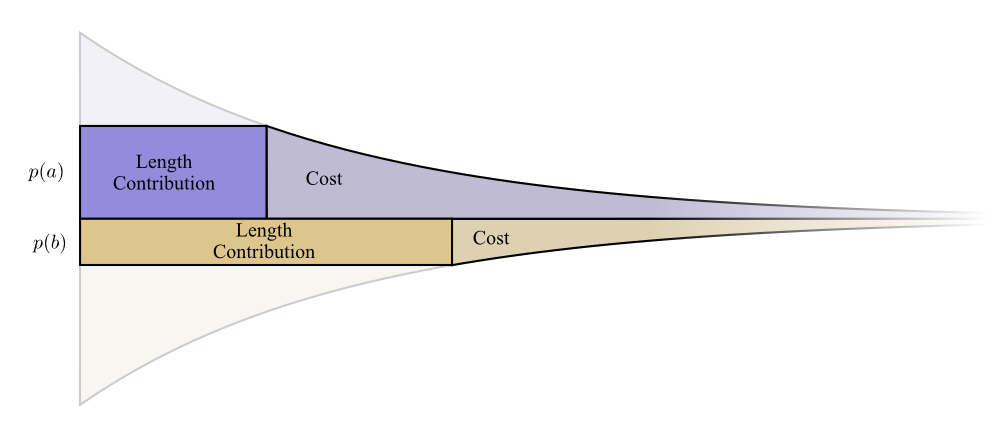

代价和长度分界线被画出了，这有任何的意义吗？
如果我们轻微改变代码词的长度，考虑一下发生了什么。如果我们轻微增加代码词的长度，信息长度分布信息长度分布将会按它边界线高度比例增加，同时代价会按照边界线高度比例减少。

因此，使得代码词a更短的代价是p(a)。同时，我们同等不关心每一个代码词的长度，我们是按我们使用它们的次数来关心它们。在a这个例子中是p(a)。把代码词a设定成1位的好处就是p(a)。
有趣的是它们的导数都是相同的。这意味着我们的初始预算有一个有趣的性质：如果你多花费一位，这对于投资使得任何代码词更短是同样有利的。我们真正关心的是好处和代价的比值——这个是决定我们应该多投资哪个的标准。在本例中，这个比例是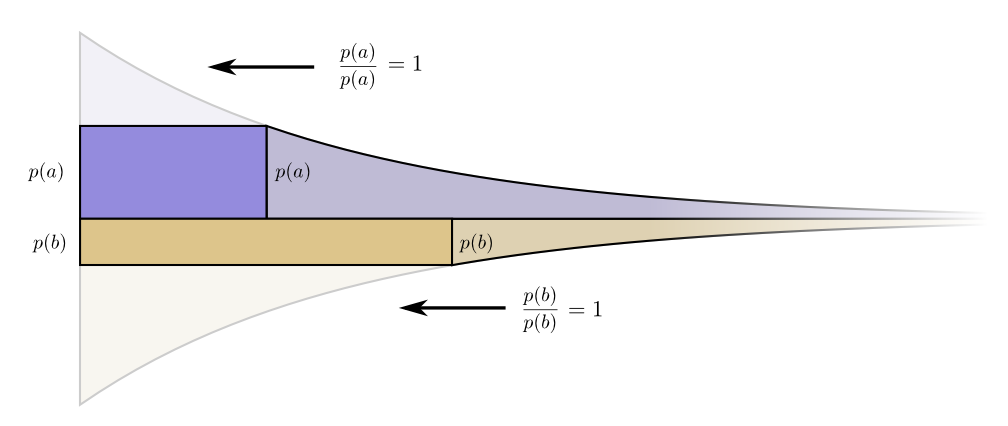p(a)p(a)，这等于1.这独立于p(a)——这个比值总是1.我们可以应用同样的参数到其他的事项中。好处/代价总是1，因此这使得对他们中的任何一个投资多1位来说是有同样的意义的。

从无穷小的角度来说，改变预算是没有意义的。但是这并不是证明这就是最佳预算。为了证明这个，我们来考虑一个不同的预算，我们以另一个为代价来对这个花费额外的一位。我们将要对b减少投资ϵ并且把它投资到a上。这使得a短了一位，b长了一位。
现在获得更短的代码词a的代价就变成了p(a)+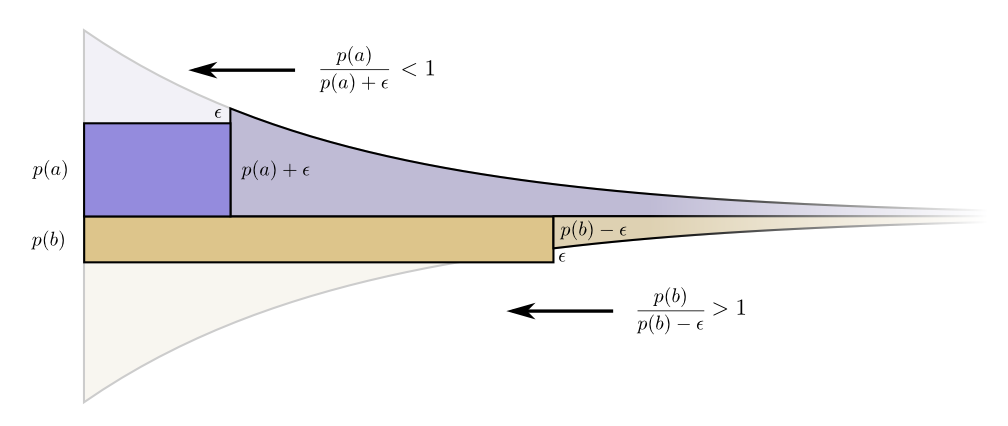ϵ，获得更短的代码词b的代价就变成了p(b)-ϵ。但是好处没有变。这就导致了a的收益代价比（如下图）小于1，同时b的收益代价比大于1。

代价就不在平衡了。b比a更好。投资人尖叫了：“买b！卖a！”我们回到了最初始的预算计划。所有的预算都可以通过移向我们的初始计划来提升。
原始的预算——按照我们使用它们的频率来投资——不仅仅是自然的，也是最优的。（尽管这个证明是针对两个代码词的，但是可以很容易的推广到多个。）
(仔细的读者可能会发现，我们的最佳预算方案会产生分数长度的编码。这好像是一个问题。这意味着什么？当然，在实践的时候，当你要发送一个编码的时候需要取整。但是我们会看到，当我们发送很多次编码的时候，能够发送分数的编码是有很重要的意义的。所以希望你能耐心的看文章的下一部分。)

计算熵值

---

回忆一下长度为L的信息的代价是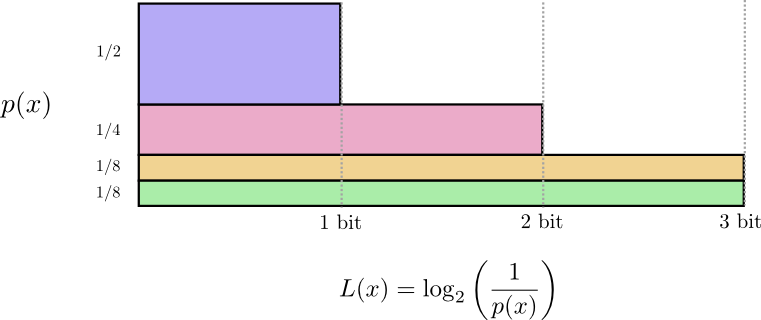12L。我们可以把这个转化为得到代价为给定的log2(1cost)信息长度。因为我们在代码词x上花了p(x)，所以长度就是log2(1p(x))。这些就是最佳的长度。

稍早的时候，我们讨论了基于一个特殊的概率分布p我们能得到用于交流的平均信息能有多短的基本的限制。这样的限制，平均信息长度使用最佳的代码，称之为p的熵值，H(p)。既然我们知道了代码词的最佳长度，我们就能够计算它！

无论我做什么，平均来说如果我想交流发生的一些事件，我需要至少去发送的这些位。
被用于交流的平均信息的数量对于压缩有明显的影响。但是这里有其他原因我需要关心的吗？是的！这描述了我多么不确定并且给了一种方式去量化信息。
如果我确实知道将会发生什么，我根本不会发送一个信息！如果有两件发生概率为50%的事情，我只需要发送一位。但是如果有64个不同的事情以同样的概率发生，我需要去发送6位。概率越集中，我就可以用更短的平均信息来制作聪明代码。
结果越不确定，平均来说，当我发现发生了什么的时候我就会学到的越多。
在Bob动身前往澳大利亚之前，他和Alice结婚了，另一个我想象的人物。令我吃惊的是Alice并不是一个狗的爱好者。她是一个猫的爱好者。尽管这样，他们两个仍然能够在他们对动物的痴迷和非常有限的词汇量中找到共同点。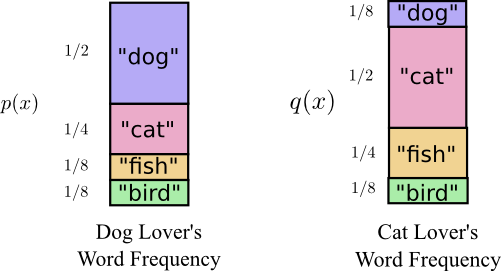

他们两个说同样的单词，仅仅是频率不同。Bob总是在说dog，Alice总是在说cat。
最初，Alice使用Bob的代码给我发消息。不幸的是她的信息太长了。Bob的代码对于他的概率分布式最优的。Alice有不同的概率分布，Bob的代码对于她来说并不是最优的。
这个长度——用一个分布的最优代码来和另一个分布交流的平均长度——被称之为交叉熵。正式的讲，我们可以定义交叉熵为：

在这个例子中，交叉熵就是Alice的单词频率关于Bob的单词频率。

代更