Codeforces Round #439 (Div. 2)（补题） A模拟+set B 数学 C dp or 杨辉三角组合数

A. The Artful Expedient

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Rock... Paper!

After Karen have found the deterministic winning (losing?) strategy for rock-paper-scissors, her brother, Koyomi, comes up with a new game as a substitute. The game works as follows.

A positive integer n is decided first. Both Koyomi and Karen independently choosen distinct positive integers, denoted by x₁, x₂, ..., x_n and y₁, y₂, ..., y_n respectively. They reveal their sequences, and repeat until all of 2n integers become distinct, which is the only final state to be kept and considered.

Then they count the number of ordered pairs (i, j) (1 ≤ i, j ≤ n) such that the valuex_ixor y_j equals to one of the2n integers. Here xor means the bitwise exclusive or operation on two integers, and is denoted by operators ^ and/or xor in most programming languages.

Karen claims a win if the number of such pairs is even, and Koyomi does otherwise. And you're here to help determine the winner of their latest game.

Input

The first line of input contains a positive integer n (1 ≤ n ≤ 2 000) — the length of both sequences.

The second line contains n space-separated integersx₁, x₂, ..., x_n (1 ≤ x_i ≤ 2·10⁶) — the integers finally chosen by Koyomi.

The third line contains n space-separated integersy₁, y₂, ..., y_n (1 ≤ y_i ≤ 2·10⁶) — the integers finally chosen by Karen.

Input guarantees that the given 2n integers are pairwise distinct, that is, no pair (i, j) (1 ≤ i, j ≤ n) exists such that one of the following holds:x_i = y_j;i ≠ j and x_i = x_j;i ≠ j and y_i = y_j.

Output

Output one line — the name of the winner, that is, "Koyomi" or "Karen" (without quotes). Please be aware of the capitalization.

Examples

Input

31 2 34 5 6

Output

Karen

Input

52 4 6 8 109 7 5 3 1

Output

Karen

Note

In the first example, there are 6 pairs satisfying the constraint:(1, 1), (1, 2), (2, 1), (2, 3), (3, 2) and(3, 3). Thus, Karen wins since 6 is an even number.

In the second example, there are 16 such pairs, and Karen wins again.

题意：问有多少对（i，j）对满足a[i]^b[j]的结果在输入中的2*n个数中出现过

思路：模拟即可，开始用map不知道怎么超时了，改用set存储。

Code：

#include <bits/stdc++.h>using namespace std;const int AX = 2e3+66;int a[AX];int b[AX];set<int>sa;set<int>sb;int main(){int n;cin >> n;for( int i = 0 ; i < n ; i++ ){cin >> a[i];sa.insert(a[i]);}for( int i = 0 ; i < n ; i++ ){cin >> b[i];sb.insert(b[i]);}int ans = 0 ;for ( int i = 0 ; i < n ; i ++ ){for( int j = 0 ; j < n ; j ++ ){int temp = ( a[i] ^ b[j] );if( sa.count(temp) || sb.count(temp) ){ans ++ ;}}}//cout << ans << endl;if( ans % 2 == 0 ){cout << "Karen" << endl;}else{cout << "Koyomi" << endl;}return 0;}

B. The Eternal Immortality

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Even if the world is full of counterfeits, I still regard it as wonderful.

Pile up herbs and incense, and arise again from the flames and ashes of its predecessor — as is known to many, the phoenix does it like this.

The phoenix has a rather long lifespan, and reincarnates itself once every a! years. Here a! denotes the factorial of integera, that is, a! = 1 × 2 × ... × a. Specifically,0! = 1.

Koyomi doesn't care much about this, but before he gets into another mess with oddities, he is interested in the number of times the phoenix will reincarnate in a timespan ofb! years, that is, 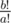. Note that whenb ≥ a this value is always integer.

As the answer can be quite large, it would be enough for Koyomi just to know the last digit of the answer in decimal representation. And you're here to provide Koyomi with this knowledge.

Input

The first and only line of input contains two space-separated integers a and b (0 ≤ a ≤ b ≤ 10¹⁸).

Output

Output one line containing a single decimal digit — the last digit of the value that interests Koyomi.

Examples

Input

2 4

Output

2

Input

0 10

Output

0

Input

107 109

Output

2

Note

In the first example, the last digit of 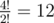is2;

In the second example, the last digit of 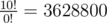is0;

In the third example, the last digit of 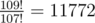is2.

题意：求b!/a!输出结果的末尾数字

思路：只要求末尾数字，已知9！的末尾为0，因此只要两个数相差大于9，结果必定是0，小于9就直接暴力算出。

Code：

→ Source #include <iostream>#include <stdio.h>#include <string.h>#include <algorithm>#define LL long longusing namespace std;int main(){LL a ,b;cin >> a >> b;if( b - a >= 9 ){cout << 0 << endl;}else{LL res = 1;for( LL i = a + 1 ; i <= b ; i++ ){res *= i;res %= 10;}cout << res << endl;}return 0;}

C. The Intriguing Obsession

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

— This is not playing but duty as allies of justice, Nii-chan!

— Not allies but justice itself, Onii-chan!

With hands joined, go everywhere at a speed faster than our thoughts! This time, the Fire Sisters — Karen and Tsukihi — is heading for somewhere they've never reached — water-surrounded islands!

There are three clusters of islands, conveniently coloured red, blue and purple. The clusters consist ofa, b andc distinct islands respectively.

Bridges have been built between some (possibly all or none) of the islands. A bridge bidirectionally connects two different islands and has length1. For any two islands of the same colour, either they shouldn't be reached from each other through bridges, or the shortest distance between them isat least 3, apparently in order to prevent oddities from spreading quickly inside a cluster.

The Fire Sisters are ready for the unknown, but they'd also like to test your courage. And you're here to figure out the number of different ways to build all bridges under the constraints, and give the answer modulo998 244 353. Two ways are considered different if a pair of islands exist, such that there's a bridge between them in one of them, but not in the other.

Input

The first and only line of input contains three space-separated integers a, b and c (1 ≤ a, b, c ≤ 5 000) — the number of islands in the red, blue and purple clusters, respectively.

Output

Output one line containing an integer — the number of different ways to build bridges, modulo998 244 353.

Examples

Input

1 1 1

Output

8

Input

1 2 2

Output

63

Input

1 3 5

Output

3264

Input

6 2 9

Output

813023575

Note

In the first example, there are 3 bridges that can possibly be built, and no setup of bridges violates the restrictions. Thus the answer is2³ = 8.

In the second example, the upper two structures in the figure below are instances of valid ones, while the lower two are invalid due to the blue and purple clusters, respectively.

题意：给出a,b,c三个岛群上的岛屿数量，要求同一个岛群上的小岛不能相连或者相连的最小距离大于3，问你有多少不同的建桥方式。

思路：由题意，同一个岛群的小岛不可能连接所以不予考虑，只考虑3个岛群之间的建桥方案，那就转换成求两两之间的组合问题了，之后再将两两之间的方案数相乘即可。

Code：

（杨辉三角版本）

#include <bits/stdc++.h>#define LL long long#define MOD  998244353using namespace std;const int AX = 5e3+6;LL f[AX];LL C[AX][AX];void init(){f[0] = 1;memset(C,0,sizeof(C));for( int i = 1 ; i < AX ; i++ ){f[i] = f[i-1] * i % MOD;}for( int i = 1 ; i < AX ; i++ ){C[i][0] = 1;C[i][i] = 1;for( int j = 1 ; j < i;  j++ ){C[i][j] = (C[i-1][j] + C[i-1][j-1])%MOD;}}}LL solve( int m , int n ){int tmp = min(m,n);LL ans = 0;for( int i = 0 ; i <= tmp ; i++ ){ans = ( ans + (1LL*C[m][i]*C[n][i])%MOD*1LL*f[i]%MOD)%MOD; //m中取i个*n中取i个*i个岛数量的阶乘}return ans ;}int main(){int a , b , c;init();cin >> a >> b >> c;LL res1 = solve(a,b) , res2 = solve(a,c) , res3 = solve(b,c);LL res = (((1LL*res1*res2)%MOD)*1LL*res3)%MOD;cout << res << endl;return 0;}

DP版本：dp[i][j] = dp[i-1][j] + dp[i-1][j-1]*i

#include <bits/stdc++.h>#define LL long long#define MOD  998244353using namespace std;const int AX = 5e3+2;LL dp[AX][AX];int main(){int a , b , c;cin >> a >> b >> c;for( int i = 0 ; i < AX ; i++ ){for( int j = 0 ; j < AX ; j++ ){if( j ){dp[i][j] = (dp[i][j]+dp[i][j-1]) % MOD;if( i ){dp[i][j] = (dp[i][j] + i * dp[i-1][j-1])%MOD;}}else{dp[i][j] = 1;}}}cout << ((* dp[a][b] * dp[a][c]) % MOD * dp[b][c])%MOD << endl;return 0;}