Educational Codeforces Round 33 E Counting Arrays（欧拉素筛+费马小定理+快速幂）

E. Counting Arrays

time limit per test

3 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

You are given two positive integer numbers x and y. An array F is called an y-factorization of x iff the following conditions are met:

• There are y elements in F, and all of them are integer numbers;
• .

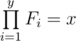You have to count the number of pairwise distinct arrays that are y-factorizations of x. Two arrays A and B are considered different iff there exists at least one index i (1 ≤ i ≤ y) such that Ai ≠ Bi. Since the answer can be very large, print it modulo 109 + 7.

Input

The first line contains one integer q (1 ≤ q ≤ 105) — the number of testcases to solve.

Then q lines follow, each containing two integers xi and yi (1 ≤ xi, yi ≤ 106). Each of these lines represents a testcase.

Output

Print q integers. i-th integer has to be equal to the number of yi-factorizations of xi modulo 109 + 7.

Example

input

26 34 2

output

366

Note

In the second testcase of the example there are six y-factorizations:

• { - 4,  - 1};
• { - 2,  - 2};
• { - 1,  - 4};
• {1, 4};
• {2, 2};
• {4, 1}.

【思路】

题目要求能连乘为x的y个数的方案数，结果对1000000007取模，大致路线是先求这y个数全部为正的方案数，然后再乘上其中存在偶数个负数的可能。那么先求x的所有质因数放入y个位置的方案数，采用隔板法，例如x含有r个质因数p，那么将r个p放入y个位置的方案数应为C(y - 1 + r, r)，然后结果再乘上其中存在若干对负数的可能，即2的(y - 1)次方。在这里思路不是问题，重点是采用恰当的方式求大组合数C(n, m) = n! / (n - m)! / (m)!，阶乘最好是递推求解，对于分子连乘即可，而对于分母，应乘以它在取模意义下的乘法逆元，在这里求乘法逆元也用了递推方式来求。在此注意一个坑点，y - 1 + r 有将可能大于1e6，所以计算范围应稍大于1e6。

【代码】

#include <cstdio>#include <cstring>#include <algorithm>using namespace std;const int MAXN = 1e6 + 30, MOD = 1e9 + 7;long long prime[MAXN], factorial[MAXN], inverse[MAXN], pow[MAXN];bool boolprime[MAXN];int t, total;long long x, y;long long qpow(long long a, long long b){    long long ans = 1;    while (b != 0) {        if (b & 1 == 1) ans = ans * a % MOD;        a = a * a % MOD;        b >>= 1;    }    return ans;}void euler(long long n){    total = 0;    memset(boolprime, false, sizeof(boolprime));    for (int i = 2; i <= n; i++) {        if (!boolprime[i]) prime[++total] = i;        for (int j = 1; j <= total && i * prime[j] <= n; j++) {            boolprime[i * prime[j]] = true;            if (i % prime[j] == 0) break;        }    }}void init(){    euler(1100);    factorial[0] = 1; pow[0] = 1;    for (int i = 1; i < MAXN; i++) {        factorial[i] = factorial[i - 1] * i % MOD;        pow[i] = pow[i - 1] * 2 % MOD;    }    inverse[MAXN - 1] = qpow(factorial[MAXN - 1], MOD - 2) % MOD;    for (int i = MAXN - 2; i >= 0; i--) inverse[i] = inverse[i + 1] * (i + 1) % MOD;}long long comb(long long n, long long m){    if (n < m) return 0;    if (n - m < m) m = n - m;    return factorial[n] * inverse[n - m] % MOD * inverse[m] % MOD;}int main(){    scanf("%d", &t);    init();    while (t--) {        scanf("%lld %lld", &x, &y);        long long ans = 1;        for (int i = 1; i <= total && prime[i] <= x; i++) {            int cnt = 0;            while (x % prime[i] == 0) {                x /= prime[i];                cnt++;            }            if (cnt >= 1) ans = ans * comb(y - 1 + cnt, cnt) % MOD;        }        if (x != 1) ans = ans * comb(y, 1) % MOD;        ans = ans * pow[y - 1] % MOD;        printf("%lld\n", ans);    }    return 0;}