二叉树--AVL树
来源:互联网 发布:linux ntp命令 编辑:程序博客网 时间:2024/06/05 06:17
AVL Tree
Time Limit: 1000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Submission(s): 642 Accepted Submission(s): 310
Problem Description
An AVL tree is a kind of balanced binary search tree. Named after their inventors, Adelson-Velskii and Landis, they were the first dynamically balanced trees to be proposed. Like red-black trees, they are not perfectly balanced, but pairs of sub-trees differ in height by at most 1, maintaining an O(logn) search time. Addition and deletion operations also take O(logn) time.
Definition of an AVL tree
An AVL tree is a binary search tree which has the following properties:
1. The sub-trees of every node differ in height by at most one.
2. Every sub-tree is an AVL tree.
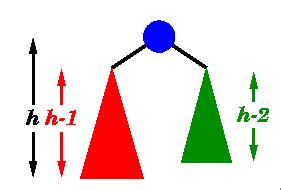
Balance requirement for an AVL tree: the left and right sub-trees differ by at most 1 in height.An AVL tree of n nodes can have different height.
For example, n = 7:
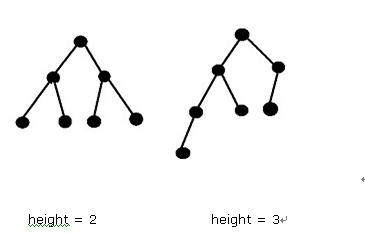
So the maximal height of the AVL Tree with 7 nodes is 3.
Given n,the number of vertices, you are to calculate the maximal hight of the AVL tree with n nodes.
Definition of an AVL tree
An AVL tree is a binary search tree which has the following properties:
1. The sub-trees of every node differ in height by at most one.
2. Every sub-tree is an AVL tree.

Balance requirement for an AVL tree: the left and right sub-trees differ by at most 1 in height.An AVL tree of n nodes can have different height.
For example, n = 7:

So the maximal height of the AVL Tree with 7 nodes is 3.
Given n,the number of vertices, you are to calculate the maximal hight of the AVL tree with n nodes.
Input
Input file contains multiple test cases. Each line of the input is an integer n(0<n<=10^9).
A line with a zero ends the input.
A line with a zero ends the input.
Output
An integer each line representing the maximal height of the AVL tree with n nodes.
Sample Input
120
Sample Output
01
Author
scnu
题意:给结点求最大深度。
#include<iostream>#include<cstdio>#include<cstring>#include<algorithm>#include<cmath>using namespace std;int a[46];int n;int main(){a[0]=1;a[1]=2;for (int i=2;i<=45;i++)a[i]=a[i-1]+a[i-2]+1;while (~scanf("%d",&n),n){int ans=0;while (a[ans]<=n) ans++;printf("%d\n",--ans);}return 0;}阅读全文
0 0
- 二叉树--AVL树
- AVL 平衡二叉树
- 平衡二叉树(AVL)
- 平衡二叉树(AVL)
- AVL 平衡二叉树
- avl平衡二叉树
- 二叉平衡树AVL
- AVL二叉查找树
- 平衡二叉树(AVL)
- 平衡二叉树(AVL)
- 平衡二叉树 AVL
- 平衡二叉树(AVL)
- 平衡二叉树(AVL)
- 平衡二叉树(AVL)
- 平衡二叉树(AVL)
- 平衡二叉树(AVL)
- 二叉平衡树AVL
- AVL平衡二叉树
- NLP大神推荐的机器学习入门书单(附大量百度网盘电子书)
- hdu 2675 Equation Again (二分)
- 1057. 数零壹(20)
- numpy 矩阵类
- 【NoSQL】宏观学习
- 二叉树--AVL树
- 范数与距离的关系以及在机器学习中的应用
- 【Java消息中间件】Java消息中间件( 第4章 使用activemq
- 我在IT职场超15年:从程序员做到副总,送你21个超实用的职场法则!
- poj3281最大流(模板)
- node.js 小功能
- Strange Printer
- LeetCode16 3Sum Closest
- 侵入式容器


