转+原：RMQ与LCA(From TopCoder Algorithm Tutorials)

原帖地址：

http://www.topcoder.com/tc?module=Static&d1=tutorials&d2=lowestCommonAncestor#Range_Minimum_Query_%28RMQ%29

RMQ(Range Minimal Query)问题

 

给定一个数组A[1..N]，RMQ(A,i,j)就是A[i..j]的最小值的下标。

 

 

 

朴素的RMQ在线算法O(N²)-O(1)

 

逐一计算出每一对（i，j）的值，存储在NXN的数组M中，算法复杂度为N*N²=N³。利用动态规划，可以降低到O(N²)。

 

voidrmq_dp(int a[],int m[][MAXN],int n){int i,j;for(i=0;i<n;i++)m[i][i]=a[i];for(i=0;i<n;i++)for(j=i+1;j<n;j++)m[i][j]=a[m[i][j-1]]>a[j]?j:m[i][j-1];}

 

时空复杂度均为O(N²)。

 

O(N)-O(sqrt(N))的一种解法

 

将数组按照每段的大小为sqrt(N）(向下取整)进行分段，则一共有sqrt(N)(向上取整)段

 

用M[0..sqrt(N)]保存每一段的最小值，复杂度为O(N)。

查询的过程先求出i,j所在段x,y

RMQ(i,j)=M[x]                    x==y

RMQ(i,j)=Min{A[i..sqrt(N)+i-1],M[x+1..y-1],A[y*sqrt(N)..j]}                        x!=y

元素个数最多不超过3sqrt(N)

 

Sparse Table algorithm（ST算法）O(N*logN)-O(1)

 

实际上也是一种DP算法，用m[i][j]来表示从下标i开始，长度为2^j的子数组的最小值，数组大小只需要m[0..N-1][0..logN]

 

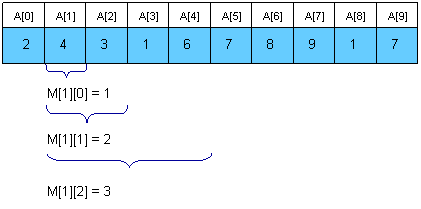
DP状态转移方程为

M[i][j]=A[i]                                                                       j=0

M[i][j]=Min{A[M[i][j-1]],A[M[i+2^j-1][j-1]]}                        j>0

voidrmq_st(int a[],int m[][LOGMAXN],int n){int i,j;for(i=0;i<n;i++)m[i][0]=a[i];for(i=0;i<n;i++)for(j=1;i+(1<<j)-1<n;j++)m[i][j]=a[m[i][j-1]]<a[m[i+(1<<(j-1))][j-1]]?m[i][j-1]:m[i+(1<<(j-1))][j-1];}

 

查询的过程需要找到能够将区间[i,j]覆盖但是又不能越界的两个m区间,采用的方法是

m[i][k]为从i开始长度为2^k的区间，m[j-2^k+1][j]为以j结束长度为2^k的区间

需要的条件是j>=i+2^k-1>=j-2^k+1

故取k=log(j-i+1)

取a[m[i][k]]和a[m[j-2^k+1][k]]中的较小的值的下标即为RMQ(i,j)

 

Segment trees 线段树 O(N)-O(logN)

解决RMQ问题也可以用Segment trees，Segment trees是一种类似堆的数据结构，定义如下

 

 

 

[0,9]的segment trees如下图所示

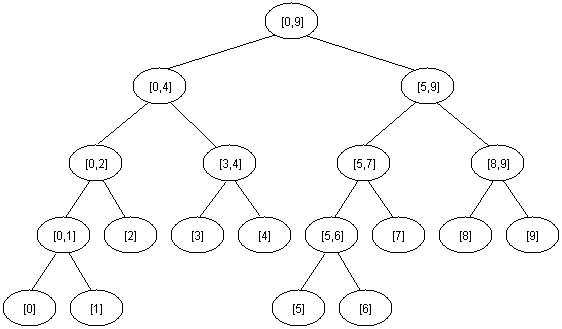
segment trees可以采用heap的数据存储结构，节点node的左儿子为节点2*node，右儿子为2*node+1

类似堆，可以用数组M[1..2*2^logN+1]来表示，对于RMQ问题，存储的区间信息就是该区间的最小值

segment trees的一个建立过程：初始调用应该是 segtree_init(1,0,N-1,m,a)

 

voidsegtree_init(int node,int b,int e,int m[],int a[]){if(b==e)m[node]=b;else{segtree_init(node*2,b,(b+e)/2,m,a);segtree_init(node*2+1,(b+e)/2+1,e,m,a);m[node]=a[m[node*2]]<a[m[node*2+1]]?m[node*2]:m[node*2+1];}}

 

查询过程

 

intseg_query(int node,int b,int e,int i,int j,int m[],int a[]){int p1,p2;if(i>e || j<b)return -1;if(i<=b && j>=e)return m[node];p1=seg_query(node*2,b,(b+e)/2,i,j,m,a);p2=seg_query(node*2+1,(b+e)/2+1,e,i,j,m,a);if(p1==-1)return p2;if(p2==-1)return p1;return a[p1]<a[p2]?p1:p2;}

比较次数为O(logN)

 

Lowest Common Ancestor (LCA问题) 这里讨论的都是在线算法

 

 一个分段解法 O(N)-O(sqrt(N))

 以sqrt(H)为大小进行分段，H为树的高度，例如

 

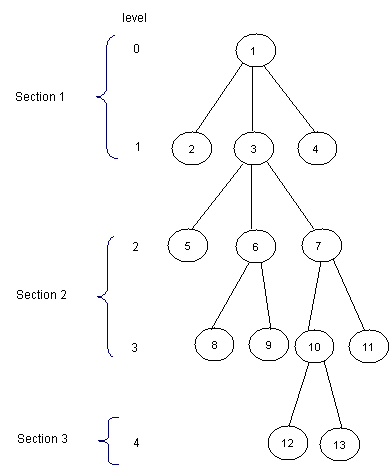
用一个深度优先遍历的顺序来预处理每个节点i

对于第一段所有的节点i，祖先是节点1，置P[i]=1

后面的每一段的最上层的节点，即深度最低的节点i，P[i]=father[i]，其他层次的节点i,P[i]=P[father[i]]

这样预处理后，每个节点都指向上一段的最低一层，即深度最高的祖先节点，对于P[i]=P[j]，节点i,j的LCS一定是P[i]或P[i]的子节点

 

 

这样，如果要查询的两个节点 (x,y) 如果P[x]=P[y] ,那么最多进行O(sqrt(H))次查询即可得到

while(x != y) if (L[x] > L[y]) x = T[x]; else y = T[y]; return x;

对于P[i]!=P[j]的，进行O(sqrt(H))次处理，使得P[x]=P[y] ,继续用上面的代码进行查询

while (P[x] != P[y]) if (L[x] > L[y]) x = P[x]; else y = P[y];

 

一共需要2*sqrt(H)次操作，最坏情况下H=N，算法最坏情况下的复杂度为O(sqrt(N))

 

另外一种简单的解法 O(NlogN)-O(logN)

 

 

仍然是DP，设P[i][j]为节点i的第 2^j 个祖先，那么有状态转移方程

P[i][0]=father[i]

P[i][j]=P[P[i][j-1]][j-1]     j>0

用2进制的思想，先使深度较高的节点2进制的阶段上升，使两个节点在同一深度上，设p,q为两个待查节点，且L(p)>L(q)，L表示p,q的深度，令log=log(L(p))，那么用log位2进制数就可以表示p的深度，从2^log开始检查，如果L(p)-2^log仍然>=L(q)，那么p=P[p][log]，上升到相应的祖先节点，log--，重复检查直到log=0。当两个节点在同一深度上，如果两个节点相等，那么直接返回，如果不相等，同样利用二进制思想，从log开始检查，如果P[p][log]！=P[q][log]，分别上升至P[p][log]和P[q][log]，循环到0的时候，必然有LCA(p,q)=father(p)

预处理复杂度为NlogN，查询复杂度为logH，最坏情况下H=N，为logN

 

从LCA到RMQ

 

 

LCA问题可以在线性时间内转化成RMQ问题，所有解决RMQ问题的方法都适用。

 

 

 

 

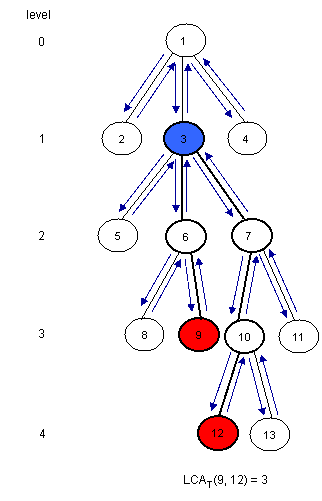
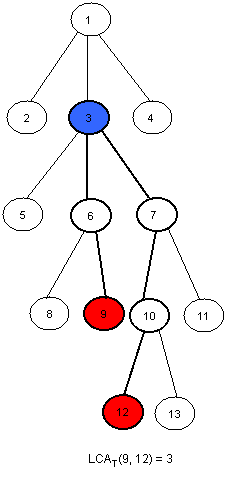
深度优先遍历树，并且记录每次访问边的端点，首先记录下根节点，那么一共有2N+1个节点被记录，用数组E[1..2N+1]来存储节点，并且用L[1..2N+1]来存储相应的节点的深度。R[1..N]来表示第一次访问节点N的数组E的下标，例如对于上图，R[9]=10,R[12]=15,而LCA(9,12)=E[RMQ(L,10,15)]。

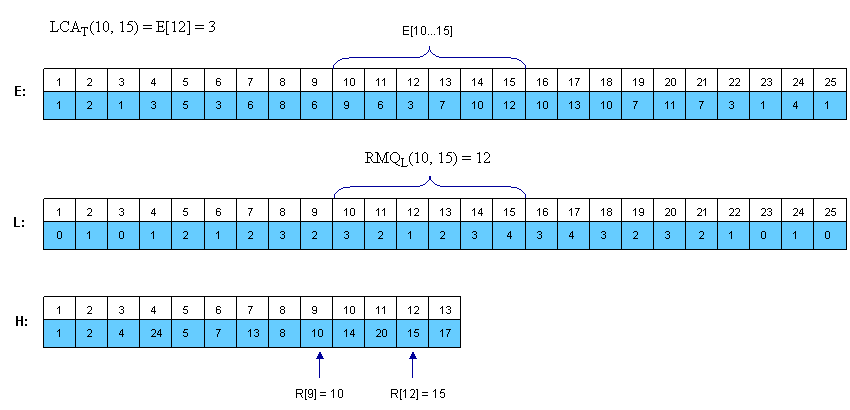
同时L数组有个特点，相邻元素的差为+-1，一般叫做+-1RMQ问题。

 

从RMQ到LCA

 

RMQ问题同样可以转换到LCA问题。这意味着一般的RMQ问题可以转换成特殊的+-1RMQ问题。我们需要用到 cartesian trees 笛卡尔树。

数组A[0..N-1]的笛卡尔树是一个以数组最小值为根的二叉树C(A)，以该最小值的下标i来标识根节点。如果i>0那么该节点的左儿子是数组A[0..i-1]的笛卡尔树，否则就没左儿子。右儿子是数组A[i+1,N-1]的笛卡尔树。如果数组里有相同的元素，该数组的笛卡尔树不是唯一的，这里相同的元素取第一个出现的，所以这里的笛卡尔树是唯一的。显然，RMQ(A,i,j)=LCA(C,i,j),示例如下

 

 

 

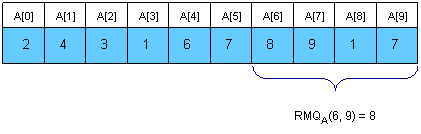
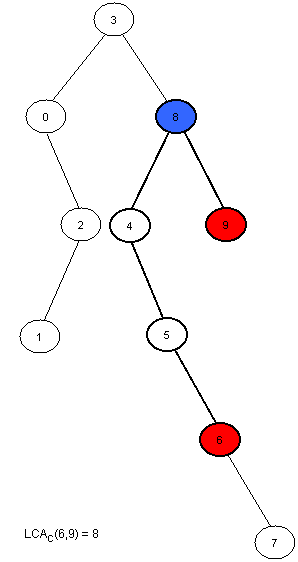
可以用栈来完成RMQ到LCA的线性时间的转化。初始栈为空，数组元素依次入栈，入栈的元素从栈底到栈顶是递增的顺序，即，如果入栈的元素i小于栈顶元素，那么栈顶元素出栈，直到栈顶元素<=当前要入栈的元素i为止，接着完成i入栈，并且i作为入栈前栈顶的右儿子，而最后出栈的元素作为i的左儿子。如此循环所有元素，最后将栈排空，最后出栈的就是根节点。

 

步 栈 修改树000是树中唯一的节点。10 1A[1]>A[0]，故1入栈，1为0的右儿子。20 2A[2]<A[1],1出栈，2入栈，2为0的右儿子，1为2的左儿子。33A[3]是数组中最小的元素，故所有元素都出栈，3为树的根。0为3的左儿子。43 44入栈，4为3的右儿子。53 4 55入栈，5为4的右儿子。63 4 5 66入栈，6为5的右儿子。73 4 5 6 77入栈，7为6的右儿子。83 88也是最小的元素，除了3所有的元素出栈，8为3的右儿子，最后出栈的4为8的左儿子。93 8 99入栈，9为8的右儿子。

T[i]表示i的父亲节点。st[]实现栈。

intrmq2lca(int *a,int n){int i,k,top;int st[MAXN];top=-1;k=top;for(i=0;i<n;i++){while(k>=0 && a[i]<a[st[k]])k--;if(k!=-1)T[i]=st[k];if(k<top)T[st[k+1]]=i;st[++k]=i;top=k;}T[st[0]]=-1;}

+-1RMQ问题的算法 O(N)-O(1)

 

现在我们知道一般的RMQ问题可以通过LCA来转化成+-1RMQ问题。我们可以利用+-1的性质来找到一个O(N)-O(1)算法。

对于数组A[1..N],相邻元素之差为+-1,那么对于所有的i,j的RMQ(A,i,j)的集合就只有 2^N 种可能性。

将问题按照大小为 I=(logN)/2 分组，故共有 N/I 组，数组 A‘ 存储每一个分块的最小值，数组 B 存储其下标，时间复杂度为O(N)。数组A'和B的大小都为N/I。现在我们用ST算法来预处理A’，时空开销都为 O(N/l*log(N/l))=O(N) 。每一个分块的大小为I，故每一个分块的RMQ就只有2^I=sqrt(N) 种可能性。计算出每一种可能性并存储在表P中，时空复杂度为O(sqrt(N)*I²)=O(N)，计算出每一个小块所属于的数组，数组类型可以用10序列来表示，即计算两个元素的差，然后用0来替换-1，复杂度为O(N)。

 

对于查询RMQ(i,j)，计算出i，j所在块x,y和块内下标a,b

 

如果x==y，则进行块内搜索，查出块x的数组类型，用a，b查询表P即可。

如果x!=y，则i，j区间分成三块，a到x块末尾，x+1到y-1块，y块开头到b,每一块的查询都是O(1)的复杂度，求出最小值即可。