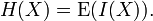信息熵 information Entropy

Introduction

Entropy is ameasureof disorder, or more precisely unpredictability. For example, a series of coin tosses with a fair coin has maximum entropy, since there is no way to predict what will come next. A string of coin tosses with a coin with two heads and no tails has zero entropy, since the coin will always come up heads. Most collections of data in the real world lie somewhere in between. It is important to realize the difference between the entropy of a set of possible outcomes, and the entropy of a particular outcome. A single toss of a fair coin has an entropy of one bit, but a particular result (e.g. "heads") has zero entropy, since it is entirely "predictable".

English text has fairly low entropy. In other words, it is fairly predictable. Even if we don't know exactly what is going to come next, we can be fairly certain that, for example, there will be many more e's than z's, or that the combination 'qu' will be much more common than any other combination with a 'q' in it and the combination 'th' will be more common than any of them. Uncompressed, English text has about onebit of entropy for each byte (eight bits) of message.^{[citation needed]}

If a compression scheme is lossless—that is, you can always recover the entire original message by uncompressing—then a compressed message has the same total entropy as the original, but in fewer bits. That is, it has more entropy per bit. This means a compressed message is more unpredictable, which is why messages are often compressed before being encrypted. Roughly speaking,Shannon's source coding theorem says that a lossless compression scheme cannot compress messages, on average, to have more than one bit of entropy per bit of message. The entropy of a message is in a certain sense a measure of how much information it really contains.

Shannon's theorem also implies that no lossless compression scheme can compress all messages. If some messages come out smaller, at least one must come out larger. In the real world, this is not a problem, because we are generally only interested in compressing certain messages, for example English documents as opposed to random bytes, or digital photographs rather than noise, and don't care if our compressor makes random messages larger.

最初定义

信息理论的鼻祖之一Claude E. Shannon把信息（熵）定义为离散随机事件的出现概率。所谓信息熵，是一个数学上颇为抽象的概念，在这里不妨把信息熵理解成某种特定信息的出现概率。

对于任意一个随机变量 X，它的熵定义如下：变量的不确定性越大，熵也就越大，把它搞清楚所需要的信息量也就越大。 　　

信息熵是信息论中用于度量信息量的一个概念。一个系统越是有序，信息熵就越低；反之，一个系统越是混乱，信息熵就越高。所以，信息熵也可以说是系统有序化程度的一个度量。

Named after Boltzmann's H-theorem, Shannon denoted the entropy H of a discrete random variable X with possible values {x₁, ...,x_n} as,

Here E is the expected value, and I is the information content of X.

I(X) is itself a random variable. If p denotes the probability mass function of X then the entropy can explicitly be written as

where b is the base of the logarithm used. Common values of b are 2, Euler's number e, and 10, and the unit of entropy isbit for b = 2,nat for b = e, and dit (or digit) for b = 10.^[3]

In the case of p_i = 0 for some i, the value of the corresponding summand 0 log_b 0 is taken to be 0, which is consistent with thelimit:

.

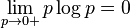The proof of this limit can be quickly obtained applying l'Hôpital's rule.

计算公式

　　H(x)=E[I(xi)]=E[ log(1/p(xi)) ]=-∑p(xi)log(p(xi)) (i=1,2,..n)

具体应用示例

1、香农指出，它的准确信息量应该是 　　= -(p1*log p1 + p2 * log p2 +　．．．　+p32 *log p32)，其中，p1，p2 ，　．．．，p32 分别是这 32 个球队夺冠的概率。香农把它称为“信息熵” (Entropy)，一般用符号 H 表示，单位是比特。有兴趣的读者可以推算一下当 32 个球队夺冠概率相同时，对应的信息熵等于五比特。有数学基础的读者还可以证明上面公式的值不可能大于五。

2、在很多情况下，对一些随机事件，我们并不了解其概率分布，所掌握的只是与随机事件有关的一个或几个随机变量的平均值。例如，我们只知道一个班的学生考试成绩有三个分数档：80分、90分、100分，且已知平均成绩为90分。显然在这种情况下，三种分数档的概率分布并不是唯一的。因为在下列已知条件限制下p1*80+p2*90+p3*100=90，P1+p2+p3=1。有无限多组解，该选哪一组解呢？即如何从这些相容的分布中挑选出“最佳的”、“最合理”的分布来呢？这个挑选标准就是最大信息熵原理。

按最大信息熵原理，我们从全部相容的分布中挑选这样的分布，它是在某些约束条件下（通常是给定的某些随机变量的平均值）使信息熵达到极大值的分布。这一原理是由杨乃斯提出的。这是因为信息熵取得极大值时对应的一组概率分布出现的概率占绝对优势。从理论上可以证明这一点。在我们把熵看作是计量不确定程度的最合适的标尺时，我们就基本已经认可在给定约束下选择不确定程度最大的那种分布作为随机变量的分布。因为这种随机分布是最为随机的，是主观成分最少，把不确定的东西作最大估计的分布。

3 Data as a Markov process

A common way to define entropy for text is based on the Markov model of text. For an order-0 source (each character is selected independent of the last characters), the binary entropy is:

where p_i is the probability of i. For a first-orderMarkov source (one in which the probability of selecting a character is dependent only on the immediately preceding character), theentropy rate is:

where i is a state (certain preceding characters) andp_i(j) is the probability ofj given i as the previous character.

For a second order Markov source, the entropy rate is

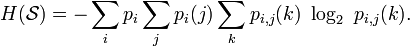
4  b-ary entropy

In general the b-ary entropy of a source 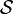= (S,P) withsource alphabet S = {a₁, ..., a_n} anddiscrete probability distribution P = {p₁, ..., p_n} where p_i is the probability of a_i (sayp_i = p(a_i)) is defined by:

Note: the b in "b-ary entropy" is the number of different symbols of the "ideal alphabet" which is being used as the standard yardstick to measure source alphabets. In information theory, two symbols arenecessary and sufficient for an alphabet to be able to encode information, therefore the default is to letb = 2 ("binary entropy"). Thus, the entropy of the source alphabet, with its given empiric probability distribution, is a number equal to the number (possibly fractional) of symbols of the "ideal alphabet", with an optimal probability distribution, necessary to encode for each symbol of the source alphabet. Also note that "optimal probability distribution" here means auniform distribution: a source alphabet with n symbols has the highest possible entropy (for an alphabet withn symbols) when the probability distribution of the alphabet is uniform. This optimal entropy turns out to be.