求回文子串 O(n) manacher算法

回文串定义：“回文串”是一个正读和反读都一样的字符串，比如“level”或者“noon”等等就是回文串。
回文子串，顾名思义，即字符串中满足回文性质的子串。
经常有一些题目围绕回文子串进行讨论，比如 HDOJ_3068_最长回文，求最长回文子串的长度。朴素算法是依次以每一个字符为中心向两侧进行扩展，显然这个复杂度是O(N^2)的，关于字符串的题目常用的算法有KMP、后缀数组、AC自动机，这道题目利用扩展KMP可以解答，其时间复杂度也很快O(N*logN)。但是，今天笔者介绍一个专门针对回文子串的算法，其时间复杂度为O(n)，这就是manacher算法。
大家都知道，求回文串时需要判断其奇偶性，也就是求aba和abba的算法略有差距。然而，这个算法做了一个简单的处理，很巧妙地把奇数长度回文串与偶数长度回文串统一考虑，也就是在每个相邻的字符之间插入一个分隔符，串的首尾也要加，当然这个分隔符不能再原串中出现，一般可以用‘#’或者‘$’等字符。例如：
原串：abaab
新串：#a#b#a#a#b#
这样一来，原来的奇数长度回文串还是奇数长度，偶数长度的也变成以‘#’为中心的奇数回文串了。
接下来就是算法的中心思想，用一个辅助数组P记录以每个字符为中心的最长回文半径，也就是P[i]记录以Str[i]字符为中心的最长回文串半径。P[i]最小为1，此时回文串为Str[i]本身。
我们可以对上述例子写出其P数组，如下
新串：#a#b#a#a#b#
P[]  : 12141252121
我们可以证明P[i]-1就是以Str[i]为中心的回文串在原串当中的长度。
证明：
1、显然2*P[i]-1即为新串中以Str[i]为中心最长回文串长度。
2、以Str[i]为中心的回文串一定是以#开头和结尾的，例如“#b#b#”或“#b#a#b#”所以L减去最前或者最后的‘#’字符就是原串中长度的二倍，即原串长度为(L-1)/2，化简的P[i]-1。得证。
依次从前往后求得P数组就可以了，这里用到了DP(动态规划)的思想，也就是求P[i]的时候，前面的P[]值已经得到了，我们利用回文串的特殊性质可以进行一个大大的优化。我先把核心代码贴上：
for(i=1;i<n;i++){if(MaxId>i){p[i]=Min(p[2*id-i],MaxId-i);}else{p[i]=1;}while(Str[i+p[i]]==Str[i-p[i]]){p[i]++;}if(p[i]+i>MaxId){MaxId=p[i]+i;id=i;}}

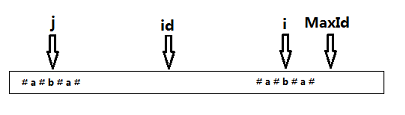
为了防止求P[i]向两边扩展时可能数组越界，我们需要在数组最前面和最后面加一个特殊字符，令P[0]=‘$’最后位置默认为‘\0’不需要特殊处理。此外，我们用MaxId变量记录在求i之前的回文串中，延伸至最右端的位置，同时用id记录取这个MaxId的id值。通过下面这句话，算法避免了很多没必要的重复匹配。
if(MaxId>i){    p[i]=Min(p[2*id-i],MaxId-i);}
那么这句话是怎么得来的呢，其实就是利用了回文串的对称性，如下图，
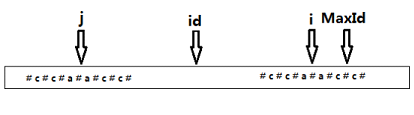
j=2*id-i即为i关于id的对称点，根据对称性，P[j]的回文串也是可以对称到i这边的,但是如果P[j]的回文串对称过来以后超过MaxId的话，超出部分就不能对称过来了，如下图，所以这里P[i]为的下限为两者中的较小者，p[i]=Min(p[2*id-i],MaxId-i)。
算法的有效比较次数为MaxId次，所以说这个算法的时间复杂度为O(n)。
附HDOJ_3068_最长回文代码：
/*-------------------------------*//* Problem: 3068/* Author:  zz_zigzag/* Date:    2012/06/05 15:59:00/*-------------------------------*/#include <stdio.h>#define M 110010char b[M],a[M<<1];int p[M<<1];int Min(int a,int b){    return a<b?a:b;}int main(){    int i,n,id,MaxL,MaxId;    while(scanf("%s",&b[1])!=EOF)    {        MaxL=MaxId=0;        for(i=1;b[i]!='\0';i++)        {            a[(i<<1)]=b[i];            a[(i<<1)+1]='#';        }        a[0]='?';a[1]='#';        n=(i<<1)+2;a[n]=0;        MaxId=MaxL=0;        for(i=1;i<n;i++)        {            if(MaxId>i)            {                p[i]=Min(p[2*id-i],MaxId-i);            }            else            {                p[i]=1;            }            while(a[i+p[i]]==a[i-p[i]])            {                p[i]++;            }            if(p[i]+i>MaxId)            {                MaxId=p[i]+i;                id=i;            }            if(p[i]>MaxL)            {                MaxL=p[i];            }        }        printf("%d\n",MaxL-1);    }    return 0;}