poj2409

Let it Bead

Description

"Let it Bead" company is located upstairs at 700 Cannery Row in Monterey, CA. As you can deduce from the company name, their business is beads. Their PR department found out that customers are interested in buying colored bracelets. However, over 90 percent of the target audience insists that the bracelets be unique. (Just imagine what happened if two women showed up at the same party wearing identical bracelets!) It's a good thing that bracelets can have different lengths and need not be made of beads of one color. Help the boss estimating maximum profit by calculating how many different bracelets can be produced. 

A bracelet is a ring-like sequence of s beads each of which can have one of c distinct colors. The ring is closed, i.e. has no beginning or end, and has no direction. Assume an unlimited supply of beads of each color. For different values of s and c, calculate the number of different bracelets that can be made.

Input

Every line of the input file defines a test case and contains two integers: the number of available colors c followed by the length of the bracelets s. Input is terminated by c=s=0. Otherwise, both are positive, and, due to technical difficulties in the bracelet-fabrication-machine, cs<=32, i.e. their product does not exceed 32.

Output

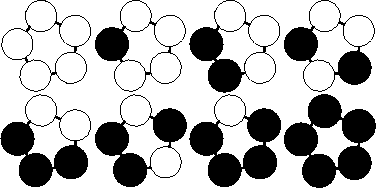For each test case output on a single line the number of unique bracelets. The figure below shows the 8 different bracelets that can be made with 2 colors and 5 beads.

Sample Input

1 12 12 25 12 52 66 20 0

Sample Output

123581321

Source

Ulm Local 2000

polya计数方法。
Polya定理:设G是n个对象的一个置换群,用m种颜色涂染这n个对象,则不同染色的方案数L=1/|G|*[m^c(a1)+m^c(a2)+....+m^c(an)].其中c(ai)是某个置换的循环数.
1.旋转置换.
我们假设依次顺时针旋转1~n个,则循环个数=gcd(i,n);
2.翻转置换
当n为偶数时,分两种情况,一种是中心轴在两个对称对象上,则循环个数为n/2+1,另一种是对称轴两边分别有n/2个对象,则循环个数为n/2;
当n为奇数时,对称轴就只能在一个对象上,则循环个数为n/2+1;
代码如下：

#include<stdio.h>  #include<math.h>    int gcd(int a,int b){      if(!b)          return a;      return gcd(b,a%b);  }    int main(void){      int c;      int s;      while(scanf("%d%d",&c,&s),s||c){          int sum=0;          for(int i=1;i<=s;i++)              sum+=pow(c,gcd(s,i));          if(s%2){              for(int i=1;i<=s;i++)              sum+=pow(c,s/2+1);          }          else{              for(int i=1;i<=s/2;i++)                  sum+=pow(c,s/2)+pow(c,s/2+1);               }          printf("%d\n",sum/2/s);      }      return 0;  }