轉置矩陣的意義

来源：互联网发布：查找算法时间复杂度编辑：程序博客网时间：2024/04/29 10:18

如果門徒向蘇格拉底提問：「轉置矩陣是甚麼？」蘇格拉底一如既往地回答：「不知道。」門徒於是轉而查閱課本的說法：

給定一 $m\times n$ 階矩陣 $A=[a_{ij}]$ ，轉置矩陣是 $n\times m$ 階矩陣，記作 $A^T$ ，其中 $(A^{T})_{ij}=a_{ji}$ 。

轉置矩陣 $A^T$ 不過就是將 $A$ 的行列對調位置而已，還有必要繼續討論下去嗎？「轉置矩陣 $A^T$ 與原矩陣 $A$ 有何關係？」誠懇向學的門徒不肯罷休又窮追猛問：「轉置矩陣 $A^T$ 有什麼代數和幾何意義？」越是基本的問題往往越難給出令多數人滿意的答案。所以先聲明：以下言論僅為個人觀點，不代表本人服務的工作單位的立場。

從矩陣的行列交換來理解轉置矩陣只是霧裡看花。相對地，逆矩陣的意義就十分明顯，因為逆矩陣的定義直接點出它的性質： $A^{-1}A=AA^{-1}=I$ ，不論解線性方程或線性變換都有直觀意義。令 $A$ 為一 $n$ 階方陣， $\mathbf{x}$ 和 $\mathbf{y}$ 為 $n$ 維向量。線性方程 $\mathbf{y}=A\mathbf{x}$ 可以解釋為 $\mathbf{x}$ 經過線性變換 $A$ 映射後得到的像 (image)。當 $A$ 是可逆時，

$\begin{aligned} A^{-1}\mathbf{y}&=A^{-1}A\mathbf{x}=I\mathbf{x}=\mathbf{x}\end{aligned}$

使用圖示可以清楚表達這個關係：

$\mathbf{x} \xrightarrow[]{~A~}\mathbf{y}\xrightarrow[]{~A^{-1}~}\mathbf{x}$

來自逆矩陣的啟發，我們不妨嘗試用線性變換觀點來認識轉置矩陣。以下設 $A$ 為 $m\times n$ 階實矩陣。既然任意矩陣 $A$ 代表一線性變換，其轉置 $A^T$ 當然也是線性變換，表面的差異是兩者的映射空間相反，即

$\begin{aligned} A&:\mathbb{R}^n\to\mathbb{R}^m\\ A^T&:\mathbb{R}^m\to\mathbb{R}^n\end{aligned}$

為便利說明，我們將 $A$ 和 $A^T$ 的關係想像為兩方在打桌球。見下圖桌球平台，圖中顯示兩個向量空間，我方 $\mathbb{R}^n$ 空間居左，對方 $\mathbb{R}^m$ 空間居右； $A$ 代表我方的球路，由左向右映射，而 $A^T$ 代表對方的球路，由右向左映射。

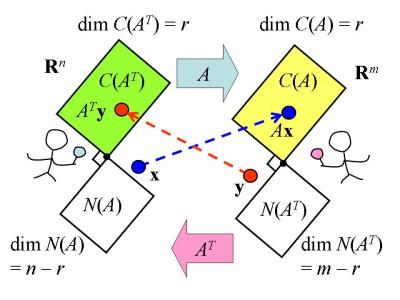
矩陣四個基本子空間分析平台

桌球平台還展示了四個主要子空間。設 $\mathbf{x}\in\mathbb{R}^n$ ， $\mathbf{y}\in\mathbb{R}^m$ 。若我方將球從 $\mathbf{x}$ 擊發，球至對方空間的落點為 $A\mathbf{x}$ ；若對方將球從 $\mathbf{y}$ 擊出，球則落於 $A^T\mathbf{y}$ 。將 $A^T$ 的行空間 (column space，即值域) ${C}(A^T)$ 想成我方球桌， $A$ 的行空間 ${C}(A)$ 為對方球桌。(在台灣，橫向稱為列，縱向稱為行。在中國大陸，橫向稱為行，縱向稱為列。) 當我方發球點 $\mathbf{x}$ 位於 $A$ 的零空間 ${N}(A)$ 內時， $A\mathbf{x}=\mathbf{0}$ 表示球彈落桌角後出界。同樣地，當對方發球點 $\mathbf{y}\in{N}(A^T)$ ，則 $A^T\mathbf{y}=\mathbf{0}$ 也表示球出界。設矩陣秩為 $r=\mathrm{rank}A$ ，則 $\mathrm{dim}{C}(A)=\mathrm{dim}{C}(A^T)=r$ ，這說明了我方球桌與對方球桌「大小」相同，都等於矩陣秩。秩—零度定理 (見“線性代數基本定理(一)”) 進一步指出 $A$ 和 $A^T$ 的行空間維度與其零度 (nullity，即零空間的維度) 的關係：

$\begin{aligned} r+\dim{N}(A)&=n\\ r+\dim{N}(A^T)&=m\end{aligned}$

到目前為止，桌球平台仍不足以完全解釋 $A$ 和 $A^T$ 的關係，我們要設法聯繫上圖顯示的四個擊球點和落點： $\mathbf{x}$ ， $A\mathbf{x}$ ， $\mathbf{y}$ ， $A^T\mathbf{y}$ 。注意， $\mathbf{x}$ 和 $A^T\mathbf{y}$ 同屬於 $\mathbb{R}^n$ 空間， $\mathbf{y}$ 和 $A\mathbf{x}$ 屬於 $\mathbb{R}^m$ 空間。我們猜想向量內積或許能夠提供一些有用的訊息，因為內積運算可以衍生向量長度的度量並建立子空間的正交關係。考慮 $\mathbb{R}^m$ 向量 $A\mathbf{x}$ 和 $\mathbf{y}$ 的內積 $(A\mathbf{x})^T\mathbf{y}=\mathbf{x}^TA^T\mathbf{y}=\mathbf{x}^T(A^T\mathbf{y})$ ，結果等於 $\mathbb{R}^n$ 向量 $\mathbf{x}$ 和 $A^T\mathbf{y}$ 的內積。數學家稱這種性質為伴隨 (adjoint)，並用它來定義轉置矩陣：給定一 $m\times n$ 階實矩陣 $A$ ， $n\times m$ 階轉置矩陣 $A^T$ 滿足

$(A\mathbf{x})^T\mathbf{y}=\mathbf{x}^T(A^T\mathbf{y})$

根據這個定義， $A^T$ 確實唯一存在嗎？存在性是無庸置疑的，我們只要證明唯一性即可。設 $B$ 和 $C$ 為 $n\times m$ 階矩陣且任意 $\mathbf{x}\in\mathbb{R}^n$ ， $\mathbf{y}\in\mathbb{R}^m$ 均滿足

$\begin{aligned} (A\mathbf{x})^T\mathbf{y}&=\mathbf{x}^T(B\mathbf{y})\\ (A\mathbf{x})^T\mathbf{y}&=\mathbf{x}^T(C\mathbf{y})\end{aligned}$

將二式相減，可得

$\begin{aligned} 0&=\mathbf{x}^T(B\mathbf{y})-\mathbf{x}^T(C\mathbf{y})=\mathbf{x}^T((B-C)\mathbf{y})\end{aligned}$

令 $\mathbf{x}=(B-C)\mathbf{y}$ ，就有 $\Vert(B-C)\mathbf{y}\Vert^2=0$ ，因為 $\mathbf{y}$ 是任意向量，故 $B-C=0$ ，證得 $A^T$ 是唯一的。

利用轉置矩陣的內積定義很容易發現子空間的正交關係 (參閱“線性代數基本定理(二)”)。考慮任一 $\mathbf{x}\in{N}(A)$ ，即 $A\mathbf{x}=\mathbf{0}$ ，則 $\mathbf{x}^T(A^T\mathbf{y})=(A\mathbf{x})^T\mathbf{y}=\mathbf{0}$ ，所以 $\mathbf{x}\perp A^T\mathbf{y}$ ，因為 $\mathbf{y}$ 是任意的，也就有 ${N}(A)\perp{C}(A^T)$ 。同樣道理也可以證得 ${N}(A^T)\perp{C}(A)$ 。再搭配秩—零度定理便推論出子空間的正交補集：

$\begin{aligned} {C}(A^T)&={N}(A)^{\perp}\\ {C}(A)&={N}(A^T)^{\perp}\end{aligned}$

以伴隨性質來定義轉置矩陣還有另外兩個目的：

(1) 內積運算比單純地把行列對調更富幾何意義。當我們從實幾何向量空間延伸至其他的向量空間，內積的定義將有所不同，所謂的伴隨形式也將隨之調整改變。例如，“內積的定義”曾經介紹複向量 $\mathbf{x},\mathbf{y}\in\mathbb{C}^n$ 的標準內積為 $\mathbf{x}^{\ast}\mathbf{y}=\overline{\mathbf{x}}^T\mathbf{y}$ ，也就有

$(A\mathbf{x})^{\ast}\mathbf{y}=(\overline{A\mathbf{x}})^T\mathbf{y}=\overline{\mathbf{x}}^T\overline{A}^T\mathbf{y}=\mathbf{x}^{\ast}(A^{\ast}\mathbf{y})$

對複矩陣 $A$ 而言，轉置必須變更為共軛轉置 (conjugate transpose) $A^{\ast}$ 方符合前述定義。

(2) 由伴隨性質出發可以輕易推論出轉置矩陣的代數性質。例如，欲證明 $(AB)^T=B^TA^T$ ，可對 $AB$ 連續使用兩次定義，先對 $A$ ，再對 $B$ ，得到

$(AB\mathbf{x})^T\mathbf{y}=(B\mathbf{x})^T(A^T\mathbf{y})=\mathbf{x}^T(B^TA^T\mathbf{y})$

將上式與 $(AB\mathbf{x})^T\mathbf{y}=\mathbf{x}^T((AB)^T\mathbf{y})$ 相比較，即證得所求。如欲證明 $(A^T)^T=A$ ，先對 $A$ 使用定義並對調位置，再對 $A^T$ 使用定義並對調位置：

$(A\mathbf{x})^T\mathbf{y}=\mathbf{x}^T(A^T\mathbf{y})=(A^T\mathbf{y})^T\mathbf{x}=\mathbf{y}^T((A^T)^T\mathbf{x})=((A^T)^T\mathbf{x})^T\mathbf{y}$

所以， $A$ 也是 $A^T$ 的轉置矩陣。

下面我們討論轉置矩陣的一個重要應用──最小平方法。見下圖，對方將球從 $\mathbf{y}\in\mathbb{R}^m$ 發出，球在我方桌面的落點為 $A^T\mathbf{y}$ 。再輪到我方發球，球從 $\mathbf{x}\in\mathbb{R}^n$ 擊出至對方桌面位置 $A\mathbf{x}$ ，對方反擊後彈回我方桌面並擊中 $A^TA\mathbf{x}$ 。如果球於我方桌面的兩次落點都在同一位置，即

$A^TA\mathbf{x}=A^T\mathbf{y}$

這代表什麼意義？上式稱為正規方程式 (normal equations)。當此式成立時， $A^T(\mathbf{y}-A\mathbf{x})=0$ ，可知 $(\mathbf{y}-A\mathbf{x})\in{N}(A^T)$ ， $A\mathbf{x}$ 正是 $\mathbf{y}$ 在對方桌面 ${C}(A)$ 的正交投影，根據正交原則，此時 $\Vert\mathbf{y}-A\mathbf{x}\Vert$ 距離最短。換句話說，我方雖未能將球直接擊中對方發球點 $\mathbf{y}$ (因為我方總是將球打向對方桌面，而 $\mathbf{y}$ 未必在對方桌面上)，但仍可令球朝著與 $\mathbf{y}$ 最接近的桌面位置擊發。當 $r=n$ 時， ${N}(A)=\{\mathbf{0}\}$ ，我方桌面 ${C}(A^T)$ 充滿了整個 $\mathbb{R}^n$ ， $n$ 階方陣 $A^TA$ 是可逆的，可得出最小平方解

$\mathbf{x}=(A^TA)^{-1}A^T\mathbf{y}$

縱使當 $r<n$ 時， $A^TA$ 不可逆，仍然可於我方桌面找到一個滿足上式的解 $\mathbf{x}$ ，比較麻煩的是這時候需要使用偽逆矩陣計算 (見“通過推導偽逆矩陣認識線性代數的深層結構”)。

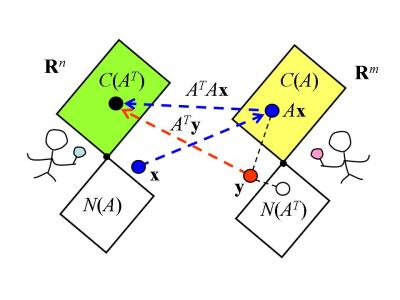
最小平方法的解釋

最後總結本文的討論：矩陣 $A$ 與其轉置 $A^T$ 的關係就像打乒乓球， $A$ 球路是「乒」， $A^T$ 球路是「乓」。我方乒過去，對方乓回來。對方是我方的「伴隨」球友，我方當然也是對方的「伴隨」球友，雙方共同遵守這條「乒乓協議」：

$(A\mathbf{x})^T\mathbf{y}=\mathbf{x}^T(A^T\mathbf{y})$

將轉置矩陣乒乓球化是我所能想到──既非十分抽象，也不過於粗淺──的解釋方法。如果讀者仍不能認同，我再提供另一個方法：想像一下，如果線性代數的世界少了轉置矩陣，哪些概念、理論和應用將因此消失？從遺失的部分反推，相信讀者也能夠建立他個人的一套轉置矩陣學說。