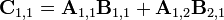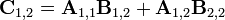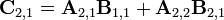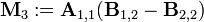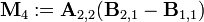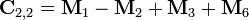程序博客网 > 淘宝app添加桌面

斯特拉森算法

来源：互联网发布：淘宝app添加桌面编辑：程序博客网时间：2024/05/14 11:00

Strassen演算法是個計算矩陣乘法的演算法。

設A, B為域 F上的方矩陣。求兩者的積C。

$\mathbf{C} = \mathbf{A} \mathbf{B} \qquad \mathbf{A},\mathbf{B},\mathbf{C} \in F^{2^n \times 2^n}$

（一般矩陣可以填0的方法計算令它成為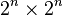 $2^n \times 2^n$ 矩陣。）

將A, B, C分成相等大小的方塊矩陣：

$\mathbf{A} =\begin{bmatrix}\mathbf{A}_{1,1} & \mathbf{A}_{1,2} \\\mathbf{A}_{2,1} & \mathbf{A}_{2,2}\end{bmatrix}\mbox { , }\mathbf{B} =\begin{bmatrix}\mathbf{B}_{1,1} & \mathbf{B}_{1,2} \\\mathbf{B}_{2,1} & \mathbf{B}_{2,2}\end{bmatrix}\mbox { , }\mathbf{C} =\begin{bmatrix}\mathbf{C}_{1,1} & \mathbf{C}_{1,2} \\\mathbf{C}_{2,1} & \mathbf{C}_{2,2}\end{bmatrix}$

即

$\mathbf{A}_{i,j}, \mathbf{B}_{i,j}, \mathbf{C}_{i,j} \in F^{2^{n-1} \times 2^{n-1}}$

於是

$\mathbf{C}_{1,1} = \mathbf{A}_{1,1} \mathbf{B}_{1,1} + \mathbf{A}_{1,2} \mathbf{B}_{2,1}$

$\mathbf{C}_{1,2} = \mathbf{A}_{1,1} \mathbf{B}_{1,2} + \mathbf{A}_{1,2} \mathbf{B}_{2,2}$

$\mathbf{C}_{2,1} = \mathbf{A}_{2,1} \mathbf{B}_{1,1} + \mathbf{A}_{2,2} \mathbf{B}_{2,1}$

$\mathbf{C}_{2,2} = \mathbf{A}_{2,1} \mathbf{B}_{1,2} + \mathbf{A}_{2,2} \mathbf{B}_{2,2}$

引入新矩陣

$\mathbf{M}_{1} := (\mathbf{A}_{1,1} + \mathbf{A}_{2,2}) (\mathbf{B}_{1,1} + \mathbf{B}_{2,2})$

$\mathbf{M}_{2} := (\mathbf{A}_{2,1} + \mathbf{A}_{2,2}) \mathbf{B}_{1,1}$

$\mathbf{M}_{3} := \mathbf{A}_{1,1} (\mathbf{B}_{1,2} - \mathbf{B}_{2,2})$

$\mathbf{M}_{4} := \mathbf{A}_{2,2} (\mathbf{B}_{2,1} - \mathbf{B}_{1,1})$

$\mathbf{M}_{5} := (\mathbf{A}_{1,1} + \mathbf{A}_{1,2}) \mathbf{B}_{2,2}$

$\mathbf{M}_{6} := (\mathbf{A}_{2,1} - \mathbf{A}_{1,1}) (\mathbf{B}_{1,1} + \mathbf{B}_{1,2})$

$\mathbf{M}_{7} := (\mathbf{A}_{1,2} - \mathbf{A}_{2,2}) (\mathbf{B}_{2,1} + \mathbf{B}_{2,2})$

可得：

$\mathbf{C}_{1,1} = \mathbf{M}_{1} + \mathbf{M}_{4} - \mathbf{M}_{5} + \mathbf{M}_{7}$

$\mathbf{C}_{1,2} = \mathbf{M}_{3} + \mathbf{M}_{5}$

$\mathbf{C}_{2,1} = \mathbf{M}_{2} + \mathbf{M}_{4}$

$\mathbf{C}_{2,2} = \mathbf{M}_{1} - \mathbf{M}_{2} + \mathbf{M}_{3} + \mathbf{M}_{6}$

其中M_{i,j}的計算也是使用Strassen演算法求得。

假定施特拉斯矩阵分割方案仅用于n>=8的矩阵乘法，而对于小于8的矩阵直接利用公式计算；n的值越大，斯拉特森方法更方便；设T(n)表示斯特拉森分治运算法所需时间，因为大的矩阵会被递归分成小矩阵直到每个矩阵的大小小于或等于k，所以T(n)的递归表达式为T(n)=d(n<=k);T(n)=7*t(n/2)+cn2(n平方）（n>k),其中cn2表示完成18次（n/2)(n/2)接矩阵的加减法，以及把大小为N的矩阵分割成小矩阵所需的时间。

淘宝app添加桌面

淘宝app添加桌面

原创粉丝点击

热门问题 老师的惩罚人脸识别我在镇武司摸鱼那些年重生之率土为王我在大康的咸鱼生活盘龙之生命进化天生仙种凡人之先天五行春回大明朝姑娘不必设防，我是瞎子黄芪的功效与作用禁忌黄苠小黄芪图片黄齐黄芪有什么功效黄芪泡水喝的功效药材黄芪黄芪的功效与作用及食用方法黄芪补什么大黄芪的功效什么是黄芪北苇作品北苑北苑小区北京北苑北苑抽粪北苑商铺北苑租房北苑站通州北苑北苑地铁站北苑新楼盘北苑的楼盘北苑学区房北苑楼盘北苑新房北苑楼盘融汇北苑北苑四合院北苑媒体村北苑在哪里景溪北苑北苑学前班华丰北苑翰林北苑北苑瑜伽馆北苑大厦锦绣北苑北苑1号院北苑医院金福北苑