牛顿法求方程根
来源:互联网 发布:三星怎么看网络电视 编辑:程序博客网 时间:2024/06/05 20:58
牛顿法
维基百科,自由的百科全书


牛顿法(Newton's method)又称为牛顿-拉弗森方法(Newton-Raphson method),它是一种在实数域和复数域上近似求解方程的方法。方法使用函数 的泰勒级数的前面几项来寻找方程
的泰勒级数的前面几项来寻找方程 的根。
的根。
目录
- 1起源
- 2方法说明
- 3其它例子
- 3.1第一个例子
- 3.2第二个例子
起源
牛顿法最初由艾萨克·牛顿在《流数法》(Method of Fluxions,1671年完成,在牛顿死后的1736年公开发表)。约瑟夫·拉弗森也曾于1690年在Analysis Aequationum中提出此方法。
方法说明

首先,选择一个接近函数 零点的
零点的 ,计算相应的
,计算相应的 和切线斜率
和切线斜率 (这里
(这里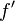 表示函数
表示函数 的导数)。然后我们计算穿过点
的导数)。然后我们计算穿过点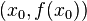 并且斜率为
并且斜率为 的直线和
的直线和 轴的交点的
轴的交点的 坐标,也就是求如下方程的解:
坐标,也就是求如下方程的解:
我们将新求得的点的 坐标命名为
坐标命名为 ,通常
,通常 会比
会比 更接近方程
更接近方程 的解。因此我们现在可以利用
的解。因此我们现在可以利用 开始下一轮迭代。迭代公式可化简为如下所示:
开始下一轮迭代。迭代公式可化简为如下所示:
已经证明,如果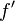 是连续的,并且待求的零点
是连续的,并且待求的零点 是孤立的,那么在零点
是孤立的,那么在零点 周围存在一个区域,只要初始值
周围存在一个区域,只要初始值 位于这个邻近区域内,那么牛顿法必定收敛。 并且,如果
位于这个邻近区域内,那么牛顿法必定收敛。 并且,如果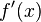 不为0, 那么牛顿法将具有平方收敛的性能. 粗略的说,这意味着每迭代一次,牛顿法结果的有效数字将增加一倍。
不为0, 那么牛顿法将具有平方收敛的性能. 粗略的说,这意味着每迭代一次,牛顿法结果的有效数字将增加一倍。
其它例子
第一个例子
求方程f(x) = cos(x) − x3的根。两边求导,得f '(x) = −sin(x) − 3x2。由于-1 ≤ cos(x) ≤ 1(对于所有x),则-1 ≤x3 ≤ 1,即-1 ≤ x ≤ 1,可知方程的根位于0和1之间。我们从x0 = 0.5开始。
第二个例子
牛顿法亦可发挥与泰勒展开式,对于函式展开的功能。
求a的m次方根。
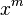 - a= 0
- a= 0
设 ,
,
而a的m次方根,亦是x的解,
以牛顿法来迭代:
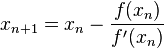
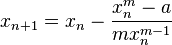

(或  )
)
- 牛顿法求方程根
- 牛顿法求方程
- 牛顿迭代法求方程根
- 牛顿迭代法求方程根
- 牛顿迭代法求方程根
- 牛顿迭代法求方程的根
- 计算方法之牛顿迭代法求方程根
- 牛顿迭代法求方程的根
- 牛顿迭代法求方程的根
- 牛顿迭代法求方程的根
- 牛顿迭代法求方程根--C语言
- 牛顿迭代法求方程解
- 3元一次方程(牛顿迭代法求方程的根)
- 计算方法-C/C++牛顿迭代法求非线性方程近似根
- 1.6_牛顿迭代法求方程的根
- 刷清橙OJ--A1094.牛顿迭代法求方程的根
- Tsinsen A1094 牛顿迭代法求方程的根
- 清橙A1094. 牛顿迭代法求方程的根
- apache mina初学,绘制的socket初始化时依赖的类图
- error C2065: “IDD_DIALOG1” : 未声明的标识符
- JAVABEN+JSP登录
- TestNG Assert 详解
- C++针对ini配置文件读写大全
- 牛顿法求方程根
- 【黑马程序员】2013年12月5日学习笔记
- 新项目中需要学习的东西
- Android系统通讯录的SQLite表的观察
- BeagleBone Black 打开CAN总线
- 8# 2013-12-5
- Windows server 2003安装软件时总提示“不能访问windows Installer服务
- 从头开始学COCOS2DX笔记三(搭建NDK环境)
- 想从测试转开发 求大神们给点建议




