【DP】HDU1950 Bridging signals——LIS最大上升子序列算法

Bridging signals

Time Limit: 5000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 499    Accepted Submission(s): 320

Problem Description

'Oh no, they've done it again', cries the chief designer at the Waferland chip factory. Once more the routing designers have screwed up completely, making the signals on the chip connecting the ports of two functional blocks cross each other all over the place. At this late stage of the process, it is too
expensive to redo the routing. Instead, the engineers have to bridge the signals, using the third dimension, so that no two signals cross. However, bridging is a complicated operation, and thus it is desirable to bridge as few signals as possible. The call for a computer program that finds the maximum number of signals which may be connected on the silicon surface without rossing each other, is imminent. Bearing in mind that there may be housands of signal ports at the boundary of a functional block, the problem asks quite a lot of the programmer. Are you up to the task?

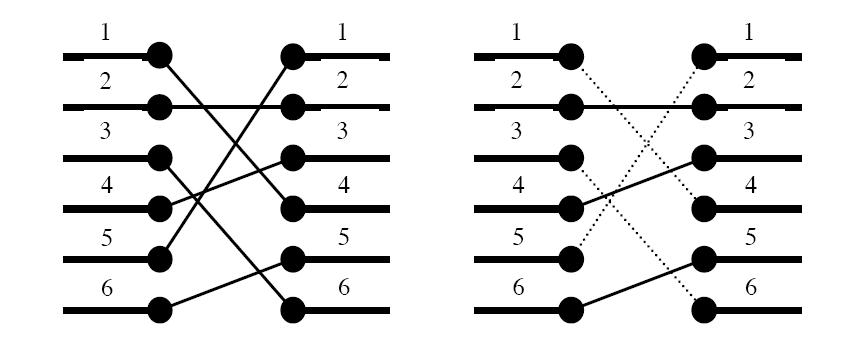
Figure 1. To the left: The two blocks' ports and their signal mapping (4,2,6,3,1,5). To the right: At most three signals may be routed on the silicon surface without crossing each other. The dashed signals must be bridged. 

A typical situation is schematically depicted in figure 1. The ports of the two functional blocks are numbered from 1 to p, from top to bottom. The signal mapping is described by a permutation of the numbers 1 to p in the form of a list of p unique numbers in the range 1 to p, in which the i:th number pecifies which port on the right side should be connected to the i:th port on the left side.
Two signals cross if and only if the straight lines connecting the two ports of each pair do.

 

Input

On the first line of the input, there is a single positive integer n, telling the number of test scenarios to follow. Each test scenario begins with a line containing a single positive integer p<40000, the number of ports on the two functional blocks. Then follow p lines, describing the signal mapping: On the i:th line is the port number of the block on the right side which should be connected to the i:th port of the block on the left side.

 

Output

For each test scenario, output one line containing the maximum number of signals which may be routed on the silicon surface without crossing each other.

 

Sample Input

4642631510234567891018876543219589231746

 

Sample Output

3914

 

 

 

 

有两种算法复杂度为 O(n＊logn) 和 O(n＾2)

O(n＾2)算法分析如下： （a［1］...a［n］ 存的都是输入的数)

1、对于a［n］来说.由于它是最后一个数，所以当从a［n］开始查找时，只存在长度为1的上升子序列；

2、若从a［n-1］开始查找.则存在下面的两种可能性：

(1)若a［n-1］ ＜ a［n］ 则存在长度为2的上升子序列 a［n-1］、a［n］；

(2)若a［n-1］ ＞ a［n］ 则存在长度为1的上升子序列 a［n-1］或者a［n］；

3、一般若从a［t］开始.此时最长上升子序列应该是按下列方法求出的：

在a［t+1］.a［t+2］… a［n］中.找出一个比a［t］大的且最长的上升子序列，作为它的后继。

4、为算法上的需要.定义一个数组dp[1 … n]记录最长上升子序列的长度，则：

dp[1] = 1;

dp[k] = Max (dp[i]:1 <= i < k 且 a[i ]< a[k] 且 k != 1) + 1.

核心代码：

dp[1] = 1;for (i = 2; i <= n; i++){temp = 0;for (j = 1; j < i; j++){if (a[i] > a[j])if (temp < dp[j])temp = dp[j];}dp[i] = temp + 1;}

最长上升子序列的O(n＊logn)算法分析如下:

先回顾经典的O(n＾2)的动态规划算法，设a[t]表示序列中的第t个数，dp[t]表示从1到t这一段中以t结尾的最长上升子序列的长度，初始时设dp [t] = 0(t = 1, 2, ..., len(a))。则有动态规划方程：dp[t] = max{1, dp[j] + 1} (j = 1, 2, ..., t - 1, 且a[j] < a[t])。

现在，我们仔细考虑计算dp[t]时的情况。假设有两个元素a[x]和a[y]，满足

(1)x < y < t

(2)a[x] < a[y] < a[t]

(3)dp[x] = dp[y]

此时，选择dp[x]和选择dp[y]都可以得到同样的dp[t]值，那么，在最长上升子序列的这个位置中，应该选择a[x]还是应该选择a[y]呢？

很明显，选择a[x]比选择a[y]要好。因为由于条件(2)，在a[x+1] ... a[t-1]这一段中，如果存在a[z]，a[x] < a[z] < a[y]，则与选择a[y]相比，将会得到更长的上升子序列。

再根据条件(3)，我们会得到一个启示：根据dp[]的值进行分类。对于dp[]的每一个取值k，我们只需要保留满足dp[t] = k的所有a[t]中的最小值。设D[k]记录这个值，即D[k] = min{a[t]} (dp[t] = k)。

注意到D[]的两个特点：

(1)　D[k]的值是在整个计算过程中是单调不上升的。

(2)　D[]的值是有序的，即D[1] < D[2] < D[3] < ... < D[n]。

利用D[]，我们可以得到另外一种计算最长上升子序列长度的方法。设当前已经求出的最长上升子序列长度为len。先判断a[t]与D[len]。若a [t] > D[len]，则将a[t]接在D[len]后将得到一个更长的上升子序列，len = len + 1， D[len] = a [t]；否则，在D[1]..D[len]中，找到最大的j，满足D[j] < a[t]。令k = j + 1，则有a [t] <= D[k]，将a[t]接在D[j]后将得到一个更长的上升子序列，更新D[k] = a[t]。最后，len即为所要求的最长上升子序列的长度。

在上述算法中，若使用朴素的顺序查找在D[1]..D[len]查找，由于共有O(n)个元素需要计算，每次计算时的复杂度是O(n)，则整个算法的时间复杂度为O(n^2)，与原来的算法相比没有任何进步。但是由于D[]的特点(2)，我们在D[]中查找时，可以使用二分查找高效地完成，则整个算法的时间复杂度下降为O(nlogn)，有了非常显著的提高。需要注意的是，D[]在算法结束后记录的并不是一个符合题意的最长上升子序列！

 

int binsearch(int x) //找到最小的大于等于它的数{int l = 1, r = len, mid;while (l <= r){mid = (l + r) >> 1;if (d[mid-1] <= x && x < d[mid]) return mid;else if (x > d[mid]) l = mid + 1;else r = mid - 1;}}int main(){scanf ("%d", &n);for (i = 1; i<= n; i++)scanf ("%d", &a[i]);memset (d, 0, sizeof (d));d[1] = a[1];len = 1;for (i = 2; i <= n; i++){if (a[i] < d[1]) j = 1;else if (a[i] > d[len]) j = ++len;else j = binsearch (a[i]);d[j] = a[i];}printf ("%d\n", len);return 0;}

 

 

解题代码：

#include<stdio.h>int map[40000],D[40000];int search(int s, int e,int j){while(s!=e){if(D[(s+e)/2]>map[j])e=(s+e)/2;elses=(s+e)/2+1;}return s;}int main(){int n,p;int i,j;int len;scanf("%d",&n);for(i=1;i<=n;i++){scanf("%d",&p);for(j=1;j<=p;j++)scanf("%d",&map[j]);len=1;D[1]=map[1];for(j=2;j<=p;j++){if(map[j]>D[len]){len++;D[len]=map[j];}elseD[search(1,len,j)]=map[j];}printf("%d\n",len);}return 0;}