Levenshtein distance

来源：互联网发布：淘宝众筹玩法编辑：程序博客网时间：2024/04/30 15:40

In information theory and computer science, the Levenshtein distance is a string metric for measuring the difference between two sequences. Informally, the Levenshtein distance between two words is the minimum number of single-character edits (i.e. insertions, deletions or substitutions) required to change one word into the other. The phrase edit distance is often used to refer specifically to Levenshtein distance. It is named after Vladimir Levenshtein, who considered this distance in 1965. It is closely related to pairwise string alignments.

Definition

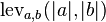Mathematically, the Levenshtein distance between two strings $a, b$ is given by $\operatorname{lev}_{a,b}(|a|,|b|)$ where

$\qquad\operatorname{lev}_{a,b}(i,j) = \begin{cases} \max(i,j) & \text{ if} \min(i,j)=0, \\ \min \begin{cases} \operatorname{lev}_{a,b}(i-1,j) + 1 \\ \operatorname{lev}_{a,b}(i,j-1) + 1 \\ \operatorname{lev}_{a,b}(i-1,j-1) + 1_{(a_i \neq b_j)} \end{cases} & \text{ otherwise.}\end{cases}$

where $1_{(a_i \neq b_j)}$ is the indicator function equal to 0 when $a_i = b_j$ and equal to 1 otherwise.

Note that the first element in the minimum corresponds to deletion (from $a$ to $b$ ), the second to insertion and the third to match or mismatch, depending on whether the respective symbols are the same.

Example

For example, the Levenshtein distance between "kitten" and "sitting" is 3, since the following three edits change one into the other, and there is no way to do it with fewer than three edits:

kitten → sitten (substitution of "s" for "k")
sitten → sittin (substitution of "i" for "e")
sittin → sitting (insertion of "g" at the end).

Computing Levenshtein distance

Recursive

A straightforward recursive implementation LevenshteinDistance function takes two strings, s and t, and returns the Levenshtein distance between them:

// len_s and len_t are the number of characters in string s and t respectivelyint LevenshteinDistance(string s, int len_s, string t, int len_t){  /* base case: empty strings */  if (len_s == 0) return len_t;  if (len_t == 0) return len_s;   /* test if last characters of the strings match */  if (s[len_s-1] == t[len_t-1]) cost = 0;  else                          cost = 1;   /* return minimum of delete char from s, delete char from t, and delete char from both */  return minimum(LevenshteinDistance(s, len_s - 1, t, len_t    ) + 1,                 LevenshteinDistance(s, len_s    , t, len_t - 1) + 1,                 LevenshteinDistance(s, len_s - 1, t, len_t - 1) + cost);}

Iterative with full matrix

Note: This section uses 1-based strings instead of 0-based strings

Computing the Levenshtein distance is based on the observation that if we reserve a matrix to hold the Levenshtein distances between all prefixes of the first string and all prefixes of the second, then we can compute the values in the matrix in a dynamic programming fashion, and thus find the distance between the two full strings as the last value computed.

This algorithm, an example of bottom-up dynamic programming, is discussed, with variants, in the 1974 article The String-to-string correction problem by Robert A. Wagner and Michael J. Fischer.^[2]

A straightforward implementation, as pseudocode for a function LevenshteinDistance that takes two strings, s of length m, and t of length n, and returns the Levenshtein distance between them:

int LevenshteinDistance(char s[1..m], char t[1..n]){  // for all i and j, d[i,j] will hold the Levenshtein distance between  // the first i characters of s and the first j characters of t;  // note that d has (m+1)*(n+1) values  declare int d[0..m, 0..n]   clear all elements in d // set each element to zero   // source prefixes can be transformed into empty string by  // dropping all characters  for i from 1 to m    {      d[i, 0] := i    }   // target prefixes can be reached from empty source prefix  // by inserting every characters  for j from 1 to n    {      d[0, j] := j    }   for j from 1 to n    {      for i from 1 to m        {          if s[i] = t[j] then            d[i, j] := d[i-1, j-1]       // no operation required          else            d[i, j] := minimum                    (                      d[i-1, j] + 1,  // a deletion                      d[i, j-1] + 1,  // an insertion                      d[i-1, j-1] + 1 // a substitution                    )        }    }   return d[m, n]}

Note that this implementation does not fit the definition precisely: it always prefers matches, even if insertions or deletions provided a better score. This is equivalent; it can be shown that for every optimal alignment (which induces the Levenshtein distance) there is another optimal alignment that prefers matches in the sense of this implementation.^[3]

Two examples of the resulting matrix (hovering over a number reveals the operation performed to get that number):

kitten 0123456s1123456i2212345t3321234t4432123i5543223n6654332g7765443 Saturday 012345678S101234567u211223456n322233456d433334345a543444434y654455543

The invariant maintained throughout the algorithm is that we can transform the initial segment s[1..i] into t[1..j] using a minimum of d[i,j] operations. At the end, the bottom-right element of the array contains the answer.

Iterative with two matrix rows

It turns out that only two rows of the table are needed for the construction if one does not want to reconstruct the edited input strings (the previous row and the current row being calculated).

The Levenshtein distance may be calculated iteratively using the following algorithm:^[8]

int LevenshteinDistance(string s, string t){    // degenerate cases    if (s == t) return 0;    if (s.Length == 0) return t.Length;    if (t.Length == 0) return s.Length;     // create two work vectors of integer distances    int[] v0 = new int[t.Length + 1];    int[] v1 = new int[t.Length + 1];     // initialize v0 (the previous row of distances)    // this row is A[0][i]: edit distance for an empty s    // the distance is just the number of characters to delete from t    for (int i = 0; i < v0.Length; i++)        v0[i] = i;     for (int i = 0; i < s.Length; i++)    {        // calculate v1 (current row distances) from the previous row v0         // first element of v1 is A[i+1][0]        //   edit distance is delete (i+1) chars from s to match empty t        v1[0] = i + 1;         // use formula to fill in the rest of the row        for (int j = 0; j < t.Length; j++)        {            var cost = (s[i] == t[j]) ? 0 : 1;            v1[j + 1] = Minimum(v1[j] + 1, v0[j + 1] + 1, v0[j] + cost);        }         // copy v1 (current row) to v0 (previous row) for next iteration        for (int j = 0; j < v0.Length; j++)            v0[j] = v1[j];    }     return v1[t.Length];}

This article comes from the Wiki. Website:点击打开链接

0 0