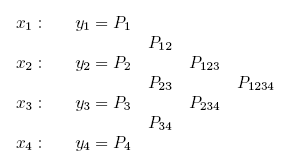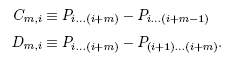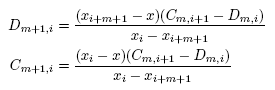Interpolation and Extrapolation（內插與外插）

插值法（內插與外插）

Interpolation and Extrapolation

 

數學問題探討

當我們在表現資料時，常常會有需要比實際量測點上的值更細密的情況，或者是有需要在範圍外預測其值。

比方說天氣圖的繪製，不論是氣壓或是雨量，都不可能做到處處都有測量站，又例如我們關心一天之中溫度隨時間的變化，但是實際上記錄氣溫的動作可能只是每小時一次，則我們要作一個連續的圖時，就會用到插值法。

插值法的中心議題是：在我們己具備一組表列數（tabulated value）的情況下， 如何得出沒被定到之區域的值。

什麼樣的函數才能被插值，這是數學上討論的間問題，參見課文 p.99 第四段。然而，我們會要用到插值法的場合往往都不知道描述對象背後的函數是什麼形式（但相信其有連續的本質），因此我們也只能盡力求真實。

使用插值法所建立的函數，在表列點上一定要重現原本給定的表列值，否則就不是插值法而是函數近似或曲線擬合的間問題了，它們是不一樣的。

插值的作法，很直觀地來講，就是，(1) 先從表列值來獲得函數 f(x)，再 (2) 用函數 f(x) 求出我們所要的任何特定 x 之 f(x) 函數值。然而，比較精密且系統化的數值方法卻不是用這兩個步驟來進行插值，原因是前述兩階段方法對於插值的精密度並沒有控制，效率較差，也比較會有進位誤差。一般在做插值法，是從欲插值點 x 附近的幾個表列點 xi 開始，建立插值函數 f(x)，並且也試著網羅更多表列點來插值，看隨著項數變多誤差會不會變小，如此找出最適合的函數 f(x)。

我們會比較希望演算法在從表列值建立插值用函數時，也能提供誤差分析以供我們或程式來判斷。畢竟可用的插值函數 f(x) 並非唯一，而即便是己設定了採用一種方法，如多項式法，也會有該使用多少項才最恰當的問題。

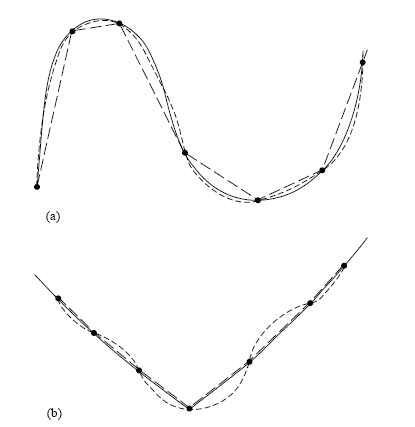
建立插值函數所需之鄰近表列值個數，我們稱之為插值法的 order（階），較高階未必保證得到較合理的插值，這點在多項式插值法尤其如此，要小心注意。詳見課文中之例圖

上兩圖實線都是原現象背後的真正值，短虛線代表低階多項式插值結果，長虛線代表高階多項式插值結果。明顯可見，case (a) 高階者較準確，而 case (b) 則是低階較準確。

 

 

線性插值法（Linear Interpolation）

所有的插值法裏面最簡單的莫過於線性插值法，任兩個相鄰的表列點之間必可以拉一條直線把它們連起來，如此在之間的 x 值就都有線性函數 y(x) 可以對應到，利用直線上的斜率必為固定值的特性，其公式是（以 (x₁,y₁)、(x₂,y₂) 為兩個相鄰的表列點為例）：

(y - y₁) / (x - x₁) = (y₂ - y₁) / (x₂ -x₁)

經整理後得

y = [ (y₂ -y₁) / (x₂ - x₁) ] (x - x₁) + y₁

注意等號的右邊全是 x 與常數，我們因此有了 y(x) 的明確公式可用。

我要求大家對於線性插值法這種較簡單的插值法，應該要能在不看參考資料的情況下做出，即自行把式子寫下來，並且把程式寫出來。

 

 

多項式插值法

大家都知道兩點唯一決定一條直線（不轉彎）、三點唯一決定一條二次曲線（會轉一次彎）、四點唯一決定一條三次曲線（會轉兩次彎，有反曲點），等等。這些曲線都是以多項式的形式（變數出現時，些是整數次方）。

一個 n - 1 次曲線的多項式雖有像 y = a_(n-1)x^(n-1) + a_(n-2)x^(n-2) + .... + a₁x +a₀ 這樣的通式可以表示出，但必須代入 n 個表列值才能定出 a_n-1 至 a₀ 那 n 個係數，一下子不易看出。

數學上有一個 Lagrange 多項式公式，它可以由 n 對 (x,y) 值唯一決定 n-1 階多項式，且公式非常好記， 如課文中的式 (3.1.1)

記法參考：寫下每一項都有係數 y_i，分母全是 (x_i - x_j)，其中 i ≠ j，分子則全部都是 (x - xj)，一樣是 i ≠ j ，這樣的項共有 N 個相加。我們的式子最高項次一定是 x^N-1，符合 (x - x_j) 連乘，並且當 x 恰為某一個 tabulated point x_i 時，y_i 會因分子分母一模一樣抵消成 1 而留下來，而其他具 y_j 的項則因其分子必定有 (x - xi) 而成為零，因此 y = y_i，符合表列值的定義。

有了上面 Lagrange polynomial 的定義，拿來寫個程式，對任給的 x 求插值，也並非不可以，只是這樣就少了誤差分析及精密度控制的動作。

真正有用的演算法，是 Neville's 演算法。它定出 P_i 為原本表列值 y_i，而 P_i(i+1) 則代表一般表列點是 x_i 與 x_i+1 所構成的一階 Lagrange 多項式。

Neville's algorithm 厲害的地方，是發現由低階多項式，可以經由組合而系統化地得出更高階多項式（例如自 P₁₂ 及 P₂₃ 得出 P₁₂₃），根據下列關係式：

另外，不同級數間的大小差異，也方便地定義了C 與 D 如何從 P 得到：

進一步推導，C 與 D 更可以從前一級的 C 與 D 得到

如此，我們再回去看上面那個橫向金字塔，比方說想要得 x 的 P₁₂₃₄，可由 低級數的 P 出發，透過 C 或 D 的求得並附加到 P 上，來獲得較高級數的 P（即在 橫向金字塔 中由左而右）越做越精密， 並且可一路上追蹤不同階數多項式之間的誤差度。