斐波那契算法分析

    学习斐波那契数列，原以为如此简单的东西不会有什么弯弯绕，网上百度了下别人的想法，没想到还是碰到了牛人，把斐波那契数列算法分析的我不得不感慨，很好很强大，转载转来，学习学习，看此算法分析前，先来看两个我今天看到的关于斐波那契的两个小知识：

    1：有10个台阶，每一步可以走一个台阶或者两个台阶，问走到第十个台阶有几种走法？

     2：斐波那契数列前一项与后一项的比值大概是多少？（当n趋于无穷的时候）

   第一道问题发现第一个台阶有一种走法，第二个台阶有两种走法，第三个台阶有三种走法，第四个台阶有五种走法，发现规律没有，符合斐波那契数列规律，所以第十个台阶有89种走法。

  第二道问题比值是0.618，这个比值是不是很熟悉，(√5-1)/2，黄金分割点，这个在股市中有着广泛的应用。

  忽然发现那些看似简单的问题其实仔细去研究都是很不简单的，下面看下转载的大牛的斐波那契的算法分析：

 

 转载：                                                                                     斐波那契数列算法分析

背景：

假定你有一雄一雌一对刚出生的兔子，它们在长到一个月大小时开始交配，在第二月结束时，雌兔子产下另一对兔子，过了一个月后它们也开始繁殖，如此这般持续下去。每只雌兔在开始繁殖时每月都产下一对兔子，假定没有兔子死亡，在一年后总共会有多少对兔子？

在一月底，最初的一对兔子交配，但是还只有1对兔子；在二月底，雌兔产下一对兔子，共有2对兔子；在三月底，最老的雌兔产下第二对兔子，共有3对兔子；在四月底，最老的雌兔产下第三对兔子，两个月前生的雌兔产下一对兔子，共有5对兔子；……如此这般计算下去，兔子对数分别是：1, 1, 2, 3, 5, 8, 13, 21, 34, 55,89, 144, ...看出规律了吗？从第3个数目开始，每个数目都是前面两个数目之和。这就是著名的斐波那契（Fibonacci）数列。

有趣问题：

1，有一段楼梯有10级台阶,规定每一步只能跨一级或两级,要登上第10级台阶有几种不同的走法?

答：这就是一个斐波那契数列：登上第一级台阶有一种登法；登上两级台阶，有两种登法；登上三级台阶，有三种登法；登上四级台阶，有五种方法……所以，1，2，3，5，8，13……登上十级，有89种。

2，数列中相邻两项的前项比后项的极限是多少，就是问，当n趋于无穷大时，F(n)/F(n+1)的极限是多少？

答：这个可由它的通项公式直接得到，极限是(-1+√5)/2，这个就是所谓的黄金分割点，也是代表大自然的和谐的一个数字。

数学表示：

Fibonacci数列的数学表达式就是：

F(n) = F(n-1) + F(n-2)

F(1) = 1

F(2) = 1

递归程序1：

Fibonacci数列可以用很直观的二叉递归程序来写，用C++语言的描述如下：

long fib1(int n)

{

     if (n <= 2)

{

     return 1;

}

else

{

     return fib1(n-1) + fib1(n-2);

}

}

看上去程序的递归使用很恰当，可是在用VC2005的环境下测试n=37的时候用了大约3s，而n=45的时候基本下楼打完饭也看不到结果……显然这种递归的效率太低了！！

递归效率分析：

例如，用下面一个测试函数：

long fib1(int n, int* arr)

{

arr[n]++;

if (n <= 2)

{

return 1;

}

else

{

return fib1(n-1, arr) + fib1(n-2, arr);

}

}

这时，可以得到每个fib(i)被计算的次数：

fib(10) = 1     fib(9) = 1      fib(8) = 2      fib(7) = 3

fib(6) = 5      fib(5) = 8      fib(4) = 13    fib(3) = 21

fib(2) = 34   fib(1) = 55    fib(0) = 34

可见，计算次数呈反向的Fibonacci数列，这显然造成了大量重复计算。

我们令T(N)为函数fib(n)的运行时间，当N>=2的时候我们分析可知：

T(N) = T(N-1) + T(N-2) + 2

而fib(n) = fib(n-1) + fib(n-2)，所以有T(N) >= fib(n)，归纳法证明可得：

fib(N) < (5/3)^N

当N>4时，fib（N）>= (3/2)^N

标准写法：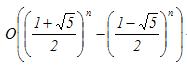

显然这个O（(3/2)^N）是以指数增长的算法，基本上是最坏的情况。

其实，这违反了递归的一个规则：合成效益法则。

合成效益法则（Compound interest rule）：在求解一个问题的同一实例的时候，切勿在不同的递归调用中做重复性的工作。

所以在上面的代码中调用fib(N-1)的时候实际上同时计算了fib(N-2)。这种小的重复计算在递归过程中就会产生巨大的运行时间。

递归程序2：

用一叉递归程序就可以得到近似线性的效率，用C++语言的描述如下：

long fib(int n, long a, long b, int count)

{

if (count == n)

return b;

return fib(n, b, a+b, ++count);

}

long fib2(int n)

{

return fib(n, 0, 1, 1);

}

这种方法虽然是递归了，但是并不直观，而且效率上相比下面的迭代循环并没有优势。

迭代解法：

Fibonacci数列用迭代程序来写也很容易，用C++语言的描述如下：

//也可以用数组将每次计算的f(n)存储下来，用来下次计算用（空间换时间）

long fib3 (int n)

{

long x = 0, y = 1;

for (int j = 1; j < n; j++)

{

y = x + y;

x = y - x;   //这里我认为原作者写错了，应该是x=y+x;

}

return y;

}

 

加一个完整的迭代如下

#include <iostream.h>void main(){  int n, i, a0, a1 ;    cout << "n = " ;    cin >> n ;    a0 = 0 ;  a1 = 1 ;    cout << a0 << '\t' << a1 << '\t';    for ( i = 2; i <= n/2 ; i ++ )      { a0 = a0 + a1 ;         a1 = a1 + a0 ;         cout << a0 << '\t' << a1 << '\t' ;         if ( i % 5 == 0 )  cout << endl ;      }    if ( n > (i-1)*2 )  cout << a0+a1 << endl ;//n为奇数，输出最后一项

} 

运行结果：

 

这时程序的效率显然为O（N），N = 45的时候<1s就能得到结果。

矩阵乘法：

我们将数列写成：

Fibonacci[0] = 0，Fibonacci[1] = 1

Fibonacci[n] = Fibonacci[n-1] + Fibonacci[n-2] (n >= 2)

可以将它写成矩阵乘法形式：

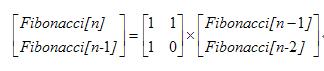
将右边连续的展开就得到：

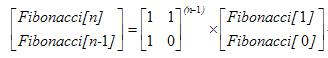
下面就是要用O(log(n))的算法计算：

显然用二分法来求，结合一些面向对象的概念，C++代码如下：

class Matrix

{

public:

       long matr[2][2];

       Matrix(const Matrix&rhs);

       Matrix(long a, long b, long c, long d);

       Matrix& operator=(const Matrix&);

       friend Matrix operator*(const Matrix& lhs, const Matrix& rhs)

       {

              Matrix ret(0,0,0,0);

              ret.matr[0][0] = lhs.matr[0][0]*rhs.matr[0][0] + lhs.matr[0][1]*rhs.matr[1][0];

              ret.matr[0][1] = lhs.matr[0][0]*rhs.matr[0][1] + lhs.matr[0][1]*rhs.matr[1][1];

              ret.matr[1][0] = lhs.matr[1][0]*rhs.matr[0][0] + lhs.matr[1][1]*rhs.matr[1][0];

              ret.matr[1][1] = lhs.matr[1][0]*rhs.matr[0][1] + lhs.matr[1][1]*rhs.matr[1][1];

              return ret;

       }

};

Matrix::Matrix(long a, long b, long c, long d)

{

       this->matr[0][0] = a;

       this->matr[0][1] = b;

       this->matr[1][0] = c;

       this->matr[1][1] = d;

}

Matrix::Matrix(const Matrix &rhs)

{

       this->matr[0][0] = rhs.matr[0][0];

       this->matr[0][1] = rhs.matr[0][1];

       this->matr[1][0] = rhs.matr[1][0];

       this->matr[1][1] = rhs.matr[1][1];

}

Matrix& Matrix::operator =(const Matrix &rhs)

{

       this->matr[0][0] = rhs.matr[0][0];

       this->matr[0][1] = rhs.matr[0][1];

       this->matr[1][0] = rhs.matr[1][0];

       this->matr[1][1] = rhs.matr[1][1];

       return *this;

}

Matrix power(const Matrix& m, int n)

{

       if (n == 1)

              return m;

       if (n%2 == 0)

              return power(m*m, n/2);

       else

              return power(m*m, n/2) * m;

}

long fib4 (int n)

{

       Matrix matrix0(1, 1, 1, 0);

       matrix0 = power(matrix0, n-1);

       return matrix0.matr[0][0];

}

这时程序的效率为O（log(N)）。

公式解法：

在O（1）的时间就能求得到F(n)了：

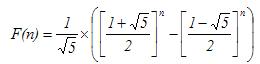
注意：其中[x]表示取距离x最近的整数。

用C++写的代码如下：

long fib5(int n)

{

double z = sqrt(5.0);

double x = (1 + z)/2;

double y = (1 - z)/2;

return (pow(x, n) - pow(y, n))/z + 0.5;

}

这个与数学库实现开方和乘方本身效率有关的，我想应该还是在O(log(n))的效率。

总结：

上面给出了5中求解斐波那契数列的方法，用测试程序主函数如下：

int main()

{

cout << fib1(45) << endl;

cout << fib2(45) << endl;

cout << fib3(45) << endl;

cout << fib4(45) << endl;

cout << fib5(45) << endl;

return 0;

}

函数fib1会等待好久，其它的都能很快得出结果，并且相同为：1134903170。

而后面两种只有在n = 1000000000的时候会显示出优势。由于我的程序都没有涉及到高精度，所以要是求大数据的话，可以通过取模来获得结果的后4位来测试效率与正确性。

另外斐波那契数列在实际工作中应该用的很少，尤其是当数据n很大的时候（例如：1000000000），所以综合考虑基本普通的非递归O(n)方法就很好了，没有必要用矩阵乘法。

 

程序全部源码：程序全部源代码：

#include <iostream> #include <vector> #include <string> #include <cmath> #include <fstream>#include<Windows.h>   using namespace std;   class Matrix { public:        long matr[2][2];          Matrix(const Matrix&rhs);        Matrix(long a, long b, long c, long d);        Matrix& operator=(const Matrix&);        friend Matrix operator*(const Matrix& lhs, const Matrix& rhs)        {               Matrix ret(0,0,0,0);               ret.matr[0][0] = lhs.matr[0][0]*rhs.matr[0][0] + lhs.matr[0][1]*rhs.matr[1][0];               ret.matr[0][1] = lhs.matr[0][0]*rhs.matr[0][1] + lhs.matr[0][1]*rhs.matr[1][1];               ret.matr[1][0] = lhs.matr[1][0]*rhs.matr[0][0] + lhs.matr[1][1]*rhs.matr[1][0];               ret.matr[1][1] = lhs.matr[1][0]*rhs.matr[0][1] + lhs.matr[1][1]*rhs.matr[1][1];               return ret;        } };   Matrix::Matrix(long a, long b, long c, long d) {        this->matr[0][0] = a;        this->matr[0][1] = b;        this->matr[1][0] = c;        this->matr[1][1] = d; }   Matrix::Matrix(const Matrix &rhs) {        this->matr[0][0] = rhs.matr[0][0];        this->matr[0][1] = rhs.matr[0][1];        this->matr[1][0] = rhs.matr[1][0];        this->matr[1][1] = rhs.matr[1][1]; }   Matrix& Matrix::operator =(const Matrix &rhs) {        this->matr[0][0] = rhs.matr[0][0];        this->matr[0][1] = rhs.matr[0][1];        this->matr[1][0] = rhs.matr[1][0];        this->matr[1][1] = rhs.matr[1][1];        return *this; }   Matrix power(const Matrix& m, int n) {        if (n == 1)               return m;        if (n%2 == 0)               return power(m*m, n/2);        else               return power(m*m, n/2) * m; }   //普通递归 long fib1(int n) {               if (n <= 2)               {                      return 1;               }               else               {                      return fib1(n-1) + fib1(n-2);               } } /*上面的效率分析代码 long fib1(int n, int* arr) {               arr[n]++;               if (n <= 1)               {                      return 1;               }               else               {                      return fib1(n-1, arr) + fib1(n-2, arr);               } } */   long fib(int n, long a, long b, int count) {        if (count == n)               return b;        return fib(n, b, a+b, ++count); } //一叉递归 long fib2(int n) {        return fib(n, 0, 1, 1); }   //非递归方法O(n) long fib3 (int n) {        long x = 0, y = 1;        for (int j = 1; j < n; j++)        {               y = x + y;               x = y - x;        }        return y; }   //矩阵乘法O(log(n)) long fib4 (int n) {        Matrix matrix0(1, 1, 1, 0);        matrix0 = power(matrix0, n-1);        return matrix0.matr[0][0]; }   //公式法O(1) long fib5(int n) {        double z = sqrt(5.0);        double x = (1 + z)/2;        double y = (1 - z)/2;        return (pow(x, n) - pow(y, n))/z + 0.5; } int main(){        //n = 45时候fib1()很慢        int n = 45;   int t=GetTickCount();        cout << fib1(n) << endl;        cout << fib2(n) << endl;        cout << fib3(n) << endl;        cout << fib4(n) << endl;        cout << fib5(n) << endl;   cout<<"fib1(n)运行时间"<<GetTickCount()-t<<"ms"<<endl;   return 0; }