hdu 4472 dp
来源:互联网 发布:java c base64 编辑:程序博客网 时间:2024/06/05 11:34
Problem Description
Prof. Tigris is the head of an archaeological team who is currently in charge of an excavation in a site of ancient relics.
This site contains relics of a village where civilization once flourished. One night, examining a writing record, you find some text meaningful to you. It reads as follows.
“Our village is of glory and harmony. Our relationships are constructed in such a way that everyone except the village headman has exactly one direct boss and nobody will be the boss of himself, the boss of boss of himself, etc. Everyone expect the headman is considered as his boss’s subordinate. We call it relationship configuration. The village headman is at level 0, his subordinates are at level 1, and his subordinates’ subordinates are at level 2, etc. Our relationship configuration is harmonious because all people at same level have the same number of subordinates. Therefore our relationship is …”
The record ends here. Prof. Tigris now wonder how many different harmonious relationship configurations can exist. He only cares about the holistic shape of configuration, so two configurations are considered identical if and only if there’s a bijection of n people that transforms one configuration into another one.
Please see the illustrations below for explanation when n = 2 and n = 4.
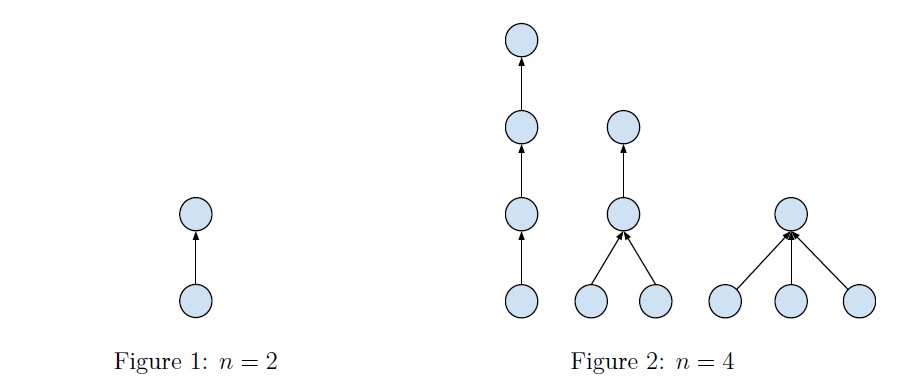
The result might be very large, so you should take module operation with modules 109 +7 before print your answer.
This site contains relics of a village where civilization once flourished. One night, examining a writing record, you find some text meaningful to you. It reads as follows.
“Our village is of glory and harmony. Our relationships are constructed in such a way that everyone except the village headman has exactly one direct boss and nobody will be the boss of himself, the boss of boss of himself, etc. Everyone expect the headman is considered as his boss’s subordinate. We call it relationship configuration. The village headman is at level 0, his subordinates are at level 1, and his subordinates’ subordinates are at level 2, etc. Our relationship configuration is harmonious because all people at same level have the same number of subordinates. Therefore our relationship is …”
The record ends here. Prof. Tigris now wonder how many different harmonious relationship configurations can exist. He only cares about the holistic shape of configuration, so two configurations are considered identical if and only if there’s a bijection of n people that transforms one configuration into another one.
Please see the illustrations below for explanation when n = 2 and n = 4.

The result might be very large, so you should take module operation with modules 109 +7 before print your answer.
Input
There are several test cases.
For each test case there is a single line containing only one integer n (1 ≤ n ≤ 1000).
Input is terminated by EOF.
For each test case there is a single line containing only one integer n (1 ≤ n ≤ 1000).
Input is terminated by EOF.
Output
For each test case, output one line “Case X: Y” where X is the test case number (starting from 1) and Y is the desired answer.
Sample Input
1234050600700
Sample Output
Case 1: 1Case 2: 1Case 3: 2Case 4: 924Case 5: 1998Case 6: 315478277Case 7: 825219749
将父节点去掉,因为这个只有一种放法,于是还剩下n-1个点。因为每一层的每个节点的子节点数相同,将这n-1个节点m等分,再递归求解。
代码:
#include <cstdio>#include <cstring>#define N 1010#define MOD 1000000007long long dp[N];int n;void DP(){ memset(dp,0,sizeof(dp)); dp[1]=1; dp[2]=1; for(int i=3; i<=1000; i++) for(int j=1; j<=i-1; j++) if((i-1)%j == 0) dp[i] = (dp[i]+dp[j])%MOD;}int main(){ DP(); int ccase=0; while(scanf("%d",&n)!=EOF) { printf("Case %d: %lld\n",++ccase,dp[n]); } return 0;}
0 0
- hdu 4472 dp
- hdu 4472 DP
- hdu 4472 Count dp
- hdu 4472 dp
- [dp] hdu 4472 Count
- hdu 4472 dp
- HDU 4472 DP
- HDU-#4472 Count(DP)
- HDU 4472 - Count(计数DP)
- HDU ACM 4472 Count->DP
- HDU DP
- DP? HDU
- DP? HDU
- DP? HDU
- 【dp】HDU
- 【dp】HDU
- 【dp】 HDU
- DP? HDU
- Android个性闹钟——摇摇醒
- linux运维常用命令
- 6.拦截器(Interceptor)
- 一点心得体会
- 在Linux(ubuntu10.10)系统中使用摄像头之USB摄像头
- hdu 4472 dp
- csu 1503: 点到圆弧的距离-湖南省第十届大学生计算机程序设计竞赛
- 程序员生存定律--升华成高手的可能方法
- 黑马程序猿_OC之三大特性
- 局部内部类访问局部变量的问题
- C语言 return多值的解决方案
- 小编程题之检测字符串表达式中括号是否配对
- php计算抽奖的概率
- elasticsearch时间格式索引管理工具: curator


