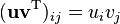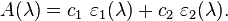化学计量学中一些重要的概念

      1.向量内积实际上是投影运算

在数学中，数量积（dot product; scalar product，也称为点积、点乘）是接受在实数R上的两个向量并返回一个实数值标量的二元运算。它是欧几里得空间的标准内积。

两个向量a = [a1, a2,…, an]和b = [b1, b2,…, bn]的点积定义为：

a·b=a1b1+a2b2+……+anbn

使用矩阵乘法并把（纵列）向量当作n×1 矩阵，点积还可以写为：

a·b=a*b^T，这里的b^T指示矩阵b的转置

  重要概念：a'(b +c)=a'b+a'c

   a'b=|a| |b| cos a

 重要概念：两个矢量的内积相当于把一个矢量投影到另外一个矢量上

 重要概念：所以坐标轴都是正交的意义是坐标轴之间互相独立，两个向量之间正交也代表两个向量独立

 问题：如果两个色谱正交，代表两个样本什么性质？代表两个样本之间完全正交，代表两个样本之间所有化合物都不同，这是非常难以做到的，所以正交是非常严格的条件

2.如何解决银杏叶中有一些掺假问题：

应用PCA算法，将高纬数据投影到低维空间上，然后根据投影的向量构成的点分类

3.inner product and outer product

 

Definition (matrix multiplication)

Main article: matrix multiplication

The outer product u ⊗ v is equivalent to a matrix multiplication uv^T, provided that u is represented as a m × 1 column vector and v as a n × 1 column vector (which makes v^T a row vector).^[1]For instance, if m = 4 and n = 3, then

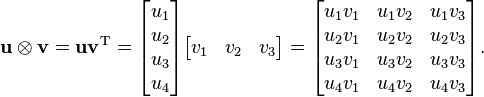
Or in index notation:

For complex vectors, it is customary to use the conjugate transpose of v (denoted v^H):

Contrast with inner product[edit]

If m = n, then one can take the matrix product the other way, yielding a scalar (or 1 × 1 matrix):

which is the standard inner product for Euclidean vector spaces, better known as the dot product. The inner product is the trace of the outer product.

Rank of an outer product[edit]

If u and v are both nonzero then the outer product matrix uv^T always has matrix rank 1, as can be easily seen by multiplying it with a vector x:

which is just a scalar v^Tx multiplied by a vector u.

("Matrix rank" should not be confused with "tensor order", or "tensor degree", which is sometimes referred to as "rank".)

4.矩阵的秩（对化学方面的意义）

1.如果物质测量的得到的矩阵只有秩为1，则证明物质中只有一个化合物

重要性质：只要知道矩阵的秩是多少，就明白这里面有多少个化合物

2.beer-lambert law  -matrix

Chemical analysis[edit]

Beer's law can be applied to the analysis of a mixture by spectrophotometry, without the need for extensive pre-processing of the sample. An example is the determination of bilirubin in blood plasma samples. The spectrum of pure bilirubin is known, so the molar attenuation coefficient is known. Measurements are made at one wavelength that is nearly unique for bilirubin and at a second wavelength in order to correct for possible interferences.The concentration is given by c = A^corrected / ε. For a more complicated example, consider a mixture in solution containing two components at concentrations c₁ and c₂. The absorbance at any wavelength, λ is, for unit path length, given by

Therefore, measurements at two wavelengths yields two equations in two unknowns and will suffice to determine the concentrations c₁ and c₂ as long as the molar absorbances of the two components, ε₁ and ε₂ are known at both wavelengths. This two system equation can be solved using Cramer's rule. In practice it is better to use linear least squares to determine the two concentrations from measurements made at more than two wavelengths. Mixtures containing more than two components can be analyzed in the same way, using a minimum of n wavelengths for a mixture containing n components. The law is used widely in infra-red spectroscopy and near-infrared spectroscopy for analysis of polymer degradation and oxidation (also in biological tissue). Thecarbonyl group attenuation at about 6 micrometres can be detected quite easily, and degree of oxidation of the polymer calculated.

5.矩阵的秩的重要意义

(1)转置后秩不变

(2)r(A)<=min(m,n),A是m*n型矩阵

(3)r(kA)=r(A),k不等于0

(4)r(A)=0 <=> A=0

(5)r(A+B)<=r(A)+r(B)

(6)r(AB)<=min(r(A),r(B))

(7)r(A)+r(B)-n<=r(AB)

特别的：A:m*n,B:n*s,AB=0 -> r(A)+r(B)<=n

(8)P,Q为可逆矩阵, 则 r(PA)=r(A)=r(AQ)=r(PAQ)