The Bookcase - POJ 3124 dp

The Bookcase

Time Limit: 3000MS Memory Limit: 65536KTotal Submissions: 1979 Accepted: 604

Description

No wonder the old bookcase caved under the massive piles of books Tom had stacked 
on it. He had better build a new one, this time large enough to hold all of his books. Tomfinds it practical to have the books close at hand when he works at his desk. Therefore, he is imagining a compact solution with the bookcase standing on the back of the desk. Obviously, this would put some restrictions on the size of the bookcase, it should preferably be as small as possible. In addition, Tom would like the bookcase to have exactly three shelves for aesthetical reasons. 

Wondering how small his bookcase could be, he models the problem as follows. He measures the height hi and thickness ti of each book i and he seeks a partition of the books in three non-empty sets S1, S2, S3 such that 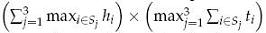is minimized, i.e. the area of the bookcase as seen when standing in front of it (the depth needed is obviously the largest width of all his books, regardless of the partition). Note that this formula does not give the exact area of the bookcase, since the actual shelves cause a small additional height, and the sides cause a small additional width. For simplicity, we will ignore this small discrepancy. 

Thinking a moment on the problem, Tom realizes he will need a computer program to do the job.

Input

The input begins with a positive number on a line of its own telling the number of test cases (at most 20). For each test case there is one line containing a single positive integer N, 3 ≤ N ≤ 70 giving the number of books. Then N lines follow each containing two positive integers hi, ti, satisfying 150 ≤ hi ≤ 300 and 5 ≤ ti ≤ 30, the height and thickness of book i respectively, in millimeters.

Output

For each test case, output one line containing the minimum area (height times width) of a three-shelf bookcase capable of holding all the books, expressed in square millimeters.

Sample Input

24220 29195 20200 9180 306256 20255 30254 15253 20252 15251 9

Sample Output

1800029796

题意：给你一些书的高度和宽度，然后有一个图中样式的一列三行书柜，要求放进去书后，三行书柜的高的和乘以书柜的宽度最小。问这个最小的面积是多少。

思路：首先我们可以假设第一行的高度为最高的那本书的高度，dp[i][j][k]表示放入第i本书后第二行的宽度为j，第三行的宽度为k时的最小高度和。每次一本书放在这三行中的一行都对应一个转移方程。首先将书按从高到低排序，只有j或k为0时才增加dp的值，另外可以用背包的思想省去i的一维。

AC代码如下：

#include<cstdio>#include<cstring>#include<algorithm>using namespace std;struct node{    int h,w;}book[100];bool cmp(node a,node b){    return a.h>b.h;}int T,t,n,dp[2200][2200],INF=1e9;int main(){    int i,j,k,a,b,p,h,x,y,W,ans,sum;    scanf("%d",&T);    for(t=1;t<=T;t++)    {        scanf("%d",&n);        W=0;        for(i=1;i<=n;i++)        {            scanf("%d%d",&book[i].h,&book[i].w);            W+=book[i].w;        }        for(j=0;j<=W;j++)           for(k=0;k<=W;k++)              dp[j][k]=INF;        sort(book+1,book+1+n,cmp);        dp[0][0]=book[1].h;        sum=book[1].w;        for(i=2;i<=n;i++)        {            for(j=sum;j>=0;j--)               for(k=sum-j;k>=0;k--)               {                   if(dp[j][k]==INF)                     continue;                   if(j==0)                     h=book[i].h;                   else                     h=0;                   dp[j+book[i].w][k]=min(dp[j+book[i].w][k],dp[j][k]+h);                   if(k==0)                     h=book[i].h;                   else                     h=0;                   dp[j][k+book[i].w]=min(dp[j][k+book[i].w],dp[j][k]+h);               }            sum+=book[i].w;        }        ans=INF;        for(j=1;j<=sum;j++)           for(k=1;k<=sum-j;k++)              if(dp[j][k]!=INF )                ans=min(ans,dp[j][k]*max(W-j-k,max(j,k)));        printf("%d\n",ans);    }}