Dome of Circus - UVa 1473 几何 凸包
来源:互联网 发布:mac diva 编辑:程序博客网 时间:2024/05/17 03:48
A travelling circus faces a tough challenge in designing the dome for its performances. The circus has a number of shows that happen above the stage in the air under the dome. Various rigs, supports, and anchors must be installed over the stage, but under the dome. The dome itself must rise above the center of the stage and has a conical shape. The space under the dome must be air-conditioned, so the goal is to design the dome that contains minimal volume.
You are given a set of n points in the space; (xi, yi, zi) for 1![]() i
i![]() n are the coordinates of the points in the air above the stage that must be covered by the dome. The ground is denoted by the plane z = 0, with positive zcoordinates going up. The center of the stage is on the ground at the point (0, 0, 0).
n are the coordinates of the points in the air above the stage that must be covered by the dome. The ground is denoted by the plane z = 0, with positive zcoordinates going up. The center of the stage is on the ground at the point (0, 0, 0).
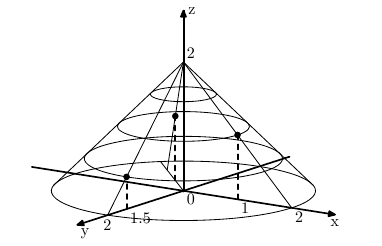
The tip of the dome must be located at some point with coordinates (0, 0, h) with h > 0. The dome must have a conical shape that touches the ground at the circle with the center in the point (0, 0, 0) and with the radius of r. The dome must contain or touch all the n given points. The dome must have the minimal volume, given the above constraints.
Input
The input file contains several test cases, each of them as described below.
The first line of the input file contains a single integer number n (1![]() n
n![]() 10000) -- the number of points under the dome. The following n lines describe points with three floating point numbers xi, yi, and zi per line -- the coordinates of i-th point. All coordinates do not exceed 1000 by their absolute value and have at most 2 digits after decimal point. All zi are positive. There is at least one point with non-zero xi or yi.
10000) -- the number of points under the dome. The following n lines describe points with three floating point numbers xi, yi, and zi per line -- the coordinates of i-th point. All coordinates do not exceed 1000 by their absolute value and have at most 2 digits after decimal point. All zi are positive. There is at least one point with non-zero xi or yi.
Output
For each test case, write to the output file a single line with two floating point numbers h and r -- the height and the base radius of the dome. The numbers must be precise up to 3 digits after decimal point.
Sample Input
1 1.00 0.00 1.00 2 1.00 0.00 1.00 0.00 1.50 0.50 3 1.00 0.00 1.00 0.00 1.50 0.50 -0.50 -0.50 1.00
Sample Output
3.000 1.500 2.000 2.000 2.000 2.000
题意:让你构造体积最小的圆锥,使得其包含给定的所有点。
思路:首先每个点都可以旋转后转化到二维平面上,然后由第一组样例可知r=1.5x,h=3y时体积最小。先求凸包,然后根据凸包上相邻两点的斜率,找最接近这个直线的情况。
AC代码如下:
#include<cstdio>#include<cstring>#include<cmath>#include<algorithm>using namespace std;struct Point{ double x,y; Point(double x=0,double y=0):x(x),y(y){} Point operator - (const Point P) const{return Point(x-P.x,y-P.y);} bool operator<(const Point P) const { if(x==P.x) return y<P.y; return x<P.x; }};double Cross(Point A,Point B){return A.x*B.y-A.y*B.x;}double getx(Point A,Point B){return (A.x*B.y-B.x*A.y)/(B.y-A.y);}double gety(Point A,Point B){return (A.x*B.y-B.x*A.y)/(A.x-B.x);}int n,m,k;Point p[10010],ch[10010];double a[10010];void ConvexHull(){ int i,j; m=0; sort(p,p+n); for(i=0;i<n;i++) { while(m>1 && Cross(ch[m-1]-ch[m-2],p[i]-ch[m-2])<=0) m--; ch[m++]=p[i]; } k=m; for(i=n-2;i>=0;i--) { while(m>k && Cross(ch[m-1]-ch[m-2],p[i]-ch[m-2])<=0) m--; ch[m++]=p[i]; } if(n>1) m--; ch[m]=ch[0];}int main(){ int i,j; double x,y,z,minn,r,h,R,H; while(~scanf("%d",&n)) { for(i=0;i<n;i++) { scanf("%lf%lf%lf",&x,&y,&z); p[i].x=sqrt(x*x+y*y); p[i].y=z; } ConvexHull(); minn=1e18; a[k-1]=ch[k-1].x; for(i=k;i<=m;i++) { if(ch[i].y<=ch[i-1].y) break; a[i]=getx(ch[i],ch[i-1]); if(1.5*ch[i-1].x<a[i-1]) r=a[i-1],h=gety(ch[i-1],Point(r,0)); else if(1.5*ch[i-1].x<a[i]) r=1.5*ch[i-1].x,h=3*ch[i-1].y; else r=a[i],h=h=gety(ch[i-1],Point(r,0)); if(r*r*h<minn) { R=r;H=h; minn=r*r*h; } } if(1.5*ch[i-1].x<a[i-1]) r=a[i-1],h=gety(ch[i-1],Point(r,0)); else r=1.5*ch[i-1].x,h=3*ch[i-1].y; if(r*r*h<minn) { R=r;H=h; minn=r*r*h; } printf("%.3f %.3f\n",H,R); }}- Dome of Circus - UVa 1473 几何 凸包
- uva 1473 - Dome of Circus (几何 + 二分)
- UVA 1473 - Dome of Circus(三分+计算几何)
- uva 1473 - Dome of Circus
- UVa 1473 Dome of Circus(求凸包)
- 圆锥:转为平面几何 UVA 1473 Dome of Circus
- HDU 3756 Dome of Circus(计算几何 + 三分)
- HDU Dome of Circus
- LA4986 Dome of Circus
- UVA1473 - Dome of Circus
- Dome of Circus POJ
- UVALive 4986 Dome of Circus(三分、凸包、凸性函数)
- HDU 3756 Dome of Circus
- 【三分】HDU3756 Dome of Circus
- Dome of Circus(三分)
- hdu3756 Dome of Circus:三分学习
- HDU 3756 Dome of Circus 三分
- hdoj 3756 Dome of Circus(三分)
- leetcode_Permutations II _hard_暴力枚举法--回溯法
- 树状数组
- PyCharm 教程(五)断点 调试
- 数据库集群技术漫谈
- 服务器负载均衡的基本功能和实现原理
- Dome of Circus - UVa 1473 几何 凸包
- 常见的连续概率密度函数
- C++ 多重继承,虚析构确定
- 一个android列表的适配器数据异步加载的问题
- 网站开发流程
- Leetcode: String to Integer (atoi)
- html+css第二课
- 用户密码的存储与 Python 示例
- Android中AsyncTask详解.


