HDU1054(最小顶点覆盖)解题报告

Strategic Game

                Time Limit: 20000/10000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)

               Total Submission(s): 5313    Accepted Submission(s): 2452

Problem Description

Bob enjoys playing computer games, especially strategic games, but sometimes he cannot find the solution fast enough and then he is very sad. Now he has the following problem. He must defend a medieval city, the roads of which form a tree. He has to put the minimum number of soldiers on the nodes so that they can observe all the edges. Can you help him?

Your program should find the minimum number of soldiers that Bob has to put for a given tree.

The input file contains several data sets in text format. Each data set represents a tree with the following description:

the number of nodes
the description of each node in the following format
node_identifier:(number_of_roads) node_identifier1 node_identifier2 ... node_identifier
or
node_identifier:(0)

The node identifiers are integer numbers between 0 and n-1, for n nodes (0 < n <= 1500). Every edge appears only once in the input data.

For example for the tree: 

 

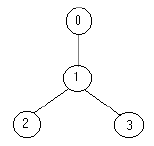
the solution is one soldier ( at the node 1).

The output should be printed on the standard output. For each given input data set, print one integer number in a single line that gives the result (the minimum number of soldiers). An example is given in the following table:

 

Sample Input

40:(1) 11:(2) 2 32:(0)3:(0)53:(3) 1 4 21:(1) 02:(0)0:(0)4:(0)

 

Sample Output

12

 

Source

Southeastern Europe 2000

 

         这道题非常经典，而且解法也比较多。

       首先来说第一种解法，即最小顶点覆盖问题。由König定理定理可知，二分图的最小顶点覆盖数等于二分图的最大匹配数。

关于König定理的证明网上也比较多。大家可以百度找一找。题目中的这棵树之所以可以当成二分图，是因为如果从一个点出发，那么可以将整棵树分成奇数点层和偶数点层。由于树是一种特殊的图。n个点由(n-1)条边连接起来。这样假定一个点为树的根，假设各点间的边权值为1。那么从树根出发遍历整棵树，根据各点到根的路径的奇偶性即可将所有点分成两个集合。奇数点与偶数点交替出现。假设奇数点与偶数点连边，偶数点则继续和下一层的奇数点连边。这就与二分图中同类集合点间无边，不同类集合点间有边相连吻合起来了。所以满足二分图的性质。也可以用二分图最大匹配进行求解。这个对点分成奇数点偶数点的方法与搜索剪枝中的奇偶剪枝很像。奇偶剪枝中对点的分类与该方法相同。

      关于奇偶剪枝，见http://blog.csdn.net/eclipse88/article/details/6475127

      奇偶剪枝经典例题：HDU1010

        下面继续说二分图最大匹配。由于对该二分图进行了补全（无向图），边增加为原来边的二倍。所以最终结果要除以2。

      二分图最小顶点覆盖=双向二分图最大匹配/2

      二分图最大匹配代码：

     

#include<cstdio>#include<cstring>#include<iostream>#include<algorithm>#include<vector>#define CLR(x) memset(x,0,sizeof(x))#define __CLR(x) memset(x,-1,sizeof(x))using namespace std;vector<int>G[1510];bool vis[1510];int match[1510];bool dfs(int u){    for(int i=0;i<G[u].size();i++)    {        int t=G[u][i];        if(!vis[t])        {            vis[t]=1;            if(match[t]==-1||dfs(match[t]))            {                match[t]=u;                return true;            }        }    }    return false;}int main(){    //ios_base::sync_with_stdio(0);    int n;    while(~scanf("%d",&n))    {        for(int i=0; i<n; i++)        {            int m,k;            scanf("%d:(%d)",&m,&k);            for(int j=0; j<k; j++)            {                int a;                scanf("%d",&a);                G[m].push_back(a);                G[a].push_back(m);            }        }        int res=0;        __CLR(match);        for(int i=0; i<n; i++)        {            CLR(vis);            if(dfs(i))                res++;        }        printf("%d\n",res/2);        for(int i=0;i<1510;i++)           G[i].clear();    }}

             方法二是树形DP。本题也是树形DP的经典例题之一。

        按照同样的方法，我们也可以对整个树进行分层，然后一层一层遍历。当然在这之前就得把无根树变成有根树。由于树本来是连通的，所以从任意一点出发均可以访问到整棵树的所有节点。首先我们找出一个点作为根，然后进行dfs遍历整棵树。进行dp的时候对于一个结点有两种决策，选择这个结点或者不选。

       如果不选择该节点作为覆盖点，那么必定要选择它的全部子节点作为覆盖点来覆盖掉与它相连的边。

       如果选择该节点作为覆盖点，那么就要考虑是否选择它的子节点，我们取优，因此选取子节点在两种决策下的最小值。

       还有要说明的是由于树的天然优良性，边为(n-1)条，很少。所以直接存储边是很明智的。存储边时采用还是邻接表存储。插入边时选取头插法。

       树形dp代码：

       

#include<cstdio>#include<cstring>#include<iostream>#include<vector>#include<algorithm>#define CLR(x) memset(x,0,sizeof(x))#define __CLR(x) memset(x,-1,sizeof(x))using namespace std;struct edge{    int to,next;}e[1505];int h[1505],dp[1505][2],num=1;void addedge(int u,int v){    e[num].to=v;    e[num].next=h[u];    h[u]=num++;}void dfs(int u){    int v,i;    dp[u][0]=0;    dp[u][1]=1;    for(i=h[u];i!=-1;i=e[i].next)    {        v=e[i].to;        dfs(v);        dp[u][0]+=dp[v][1];        dp[u][1]+=min(dp[v][0],dp[v][1]);    }}int main(){    int n;    while(~scanf("%d",&n))    {        __CLR(h);        int rt=-1;        num=1;        for(int i=1; i<=n; i++)        {            int u,k;            scanf("%d:(%d)",&u,&k);            for(int j=1; j<=k; j++)            {                int v;                scanf("%d",&v);                addedge(u,v);            }            if(rt==-1) rt=u;        }        dfs(rt);        int res=min(dp[rt][0],dp[rt][1]);        printf("%d\n",res);    }}

          方法三就是贪心。贪心的策略是选择点的度数越多的点价值越高。度数为1的点价值最小。当然我们可以找出与度数为1的点相连的那些点作为覆盖点。并删除与这些点相连的边。这个方法与拓扑排序的思想有很大的相似性。从结点的度上入手考虑，并记录每个结点的度数，在进行完决策后进行删边操作，直到最终没有点的度为1为止。进行操作时可以用队列实现。感觉与拓扑排序真的好像。虽然目的不同，但思想相通。

      用visit数组记录结点是否被访问过，保证每个结点被访问一次。（边是无向边）

      贪心代码：

      

#include<cstdio>#include<cstring>#include<iostream>#include<vector>#include<queue>#include<algorithm>#define CLR(x) memset(x,0,sizeof(x))#define __CLR(x) memset(x,-1,sizeof(x))#define pb push_backusing namespace std;vector<int>G[1505];int indx[1505],vis[1505],n;void solve(){    CLR(vis);    queue<int> q;    for(int i=0; i<n; i++)        if(indx[i]==1)            q.push(i);    int num=0;    while(!q.empty())    //因为是树，具有连通性，不会导致死循环    {        int s=q.front();        q.pop();        if(!vis[s])        {            vis[s]=1;            for(int i=0; i<G[s].size(); i++)            {                int t=G[s][i];                if(!vis[t])                {                    num++;                    vis[t]=1;              //此处为何没有考虑t点的度是等于1还是大于1呢？试想如果等于1，那么选s点与t点都行，                    //但是如果大于1,那么肯定选t点了。这一点与König定理定理证明时选择那个匹配点更优的思想很像                    for(int j=0; j<G[t].size(); j++)                    {                        int tt=G[t][j];                        indx[tt]--;                        if(indx[tt]==1&&!vis[tt])                            q.push(tt);                    }                }            }        }    }    printf("%d\n",num);}int main(){    while(~scanf("%d",&n))    {        CLR(indx);        for(int i=0; i<n; i++)        {            int u,k;            scanf("%d:(%d)",&u,&k);            for(int j=1; j<=k; j++)            {                int v;                scanf("%d",&v);                G[u].pb(v);                G[v].pb(u);                indx[u]++;                indx[v]++;            }        }        if(n==1)        {            printf("1\n");            continue;        }        solve();        for(int i=0;i<1505;i++)            G[i].clear();    }}

          这道题一题多解，涉及的知识面很广，不得不钻研一下。