Codeforces Round #261 (Div. 2) E. Pashmak and Graph （sorting + dp）

E. Pashmak and Graph
time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Pashmak's homework is a problem about graphs. Although he always tries to do his homework completely, he can't solve this problem. As you know, he's really weak at graph theory; so try to help him in solving the problem.

You are given a weighted directed graph with n vertices andm edges. You need to find a path (perhaps, non-simple) with maximum number of edges, such that the weights of the edges increase along the path. In other words, each edge of the path must have strictly greater weight than the previous edge in the path.

Help Pashmak, print the number of edges in the required path.

Input

The first line contains two integers n,m (2 ≤ n ≤ 3·10⁵; 1 ≤ m ≤ min(n·(n - 1), 3·10⁵)). Then,m lines follows. The i-th line contains three space separated integers: u_i, v_i, w_i (1 ≤ u_i, v_i ≤ n; 1 ≤ w_i ≤ 10⁵) which indicates that there's a directed edge with weight w_i from vertexu_i to vertexv_i.

It's guaranteed that the graph doesn't contain self-loops and multiple edges.

Output

Print a single integer — the answer to the problem.

Sample test(s)

Input

3 31 2 12 3 13 1 1

Output

1

Input

3 31 2 12 3 23 1 3

Output

3

Input

6 71 2 13 2 52 4 22 5 22 6 95 4 34 3 4

Output

6

Note

In the first sample the maximum trail can be any of this trails: .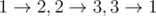

In the second sample the maximum trail is .

In the third sample the maximum trail is .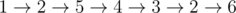

解析：先将所有边按权值从小到大排序，然后再按权值递增dp。

AC代码：

#include <bits/stdc++.h>using namespace std;const int N = 300005;struct edge{    int x, y, w;    void in(){        scanf("%d%d%d", &x, &y, &w);    }    bool operator <(const edge &a) const{        return w < a.w;    }} E[N];int dp[N];int main(){    #ifdef sxk        freopen("in.txt", "r", stdin);    #endif // sxk    int n, m;    while(scanf("%d%d", &n, &m)!=EOF){        memset(dp, 0, sizeof(dp));        for(int i=0; i<m; i++) E[i].in();        sort(E, E + m);        int ans = 0;        int cur = E[0].w;        for(int i=0; i<m; ){            vector<pair<int, int> > p;            while(E[i].w == cur){                int foo = max(dp[ E[i].y ], dp[ E[i].x ] + 1);                ans = max(ans, foo);                p.push_back(make_pair(E[i].y, foo));                i ++;            }            for(int j=0; j<p.size(); j++){                dp[ p[j].first ] = max(dp[ p[j].first ], p[j].second);            }            cur = E[i].w;        }        printf("%d\n", ans);    }    return 0;}