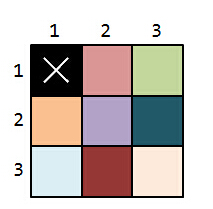hdu 5301 Buildings 2015 Buildings Multi-University Training Contest 2



Buildings

Time Limit: 4000/2000 MS (Java/Others)    Memory Limit: 131072/131072 K (Java/Others)
Total Submission(s): 979    Accepted Submission(s): 281

Problem Description

Your current task is to make a ground plan for a residential building located in HZXJHS. So you must determine a way to split the floor building with walls to make apartments in the shape of a rectangle. Each built wall must be paralled to the building's sides.

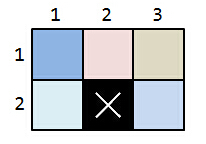
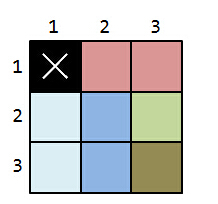
The floor is represented in the ground plan as a large rectangle with dimensions n×m, where each apartment is a smaller rectangle with dimensions a×b located inside. For each apartment, its dimensions can be different from each other. The numbera and b must be integers.

Additionally, the apartments must completely cover the floor without one 1×1 square located on (x,y). The apartments must not intersect, but they can touch.

For this example, this is a sample of n=2,m=3,x=2,y=2.



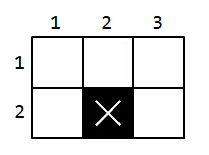
To prevent darkness indoors, the apartments must have windows. Therefore, each apartment must share its at least one side with the edge of the rectangle representing the floor so it is possible to place a window.

Your boss XXY wants to minimize the maximum areas of all apartments, now it's your turn to tell him the answer.

 

Input

There are at most 10000 testcases.
For each testcase, only four space-separated integers, n,m,x,y(1≤n,m≤108,n×m>1,1≤x≤n,1≤y≤m).

 

Output

For each testcase, print only one interger, representing the answer.

 

Sample Input

2 3 2 23 3 1 1

 

Sample Output

12
Hint
Case 1 :You can split the floor into five 1×1 apartments. The answer is 1.Case 2:You can split the floor into three 2×1 apartments and two 1×1 apartments. The answer is 2.If you want to split the floor into eight 1×1 apartments, it will be unacceptable because the apartment located on (2,2) can't have windows.
 

 

Source

2015 Multi-University Training Contest 2

 

Recommend

wange2014

 

证明一个有关不等式的结论：

令min(   up,down )=k;

那么有max(    min(  left,k+1  ),min( right,K+1 )     )=min(    max(left,right)   ,K+1          );

当left=right时，左边=max( min(left,K+1),min(left,K+1)  )=max(min(left,K+1))=min(left,K+1),右边=min(left,K+1)=左边;  显然成立

当left!=right  ,不妨设left<right   

( 引理：若b<c,则max(a1,a2,...,an,b)<=max(a1,a2,...,b,...,an,c )  ,若将max改为min依然成立;   )

  因为 min(left,K+1)<=min(  right,K+1         )，所以左边<=max(  min(right,K+1),right(right,K+1) )=max(min(right,K+1) )=min(right,k+1);

而左边>=min(right,K+1),所以左边=min(  min(right,K+1));

因为left<right,右边=min(right  ,K+1)，

故左右相等。证毕

若将上式max 改为min，min改为max仍成立。

对于一个正整数x,y，线段x到y 二分中较长一段 长度为(x+y)/2;

对于每一个位置的坏点，代码综合考虑了对四个方向的点造成的影响。

#include<cstdio>#include<string>#include<cstring>#include<iostream>#include<cmath>#include<algorithm>#include<climits>#include<queue>#include<vector>#include<map>#include<sstream>#include<set>#include<stack>#include<utility>//#pragma comment(linker, "/STACK:102400000,102400000")#define INF 0x3f3f3f3f#define PI 3.1415926535897932384626#define eps 1e-10#define sqr(x) ((x)*(x))#define FOR0(i,n)  for(int i=0 ;i<(n) ;i++)#define FOR1(i,n)  for(int i=1 ;i<=(n) ;i++)#define FORD(i,n)  for(int i=(n) ;i>=0 ;i--)#define  lson   num<<1,l,mid#define rson    num<<1|1,mid+1,r#define MID   int mid=(l+r)>>1using namespace std;//const int maxn=    ;//const int maxm=    ;//const int INF=    ;//typedef long long ll;//ifstream fin("input.txt");//ofstream fout("output.txt");//fin.close();//fout.close();int n,m,x,y;int main(){//    freopen("in.txt","r",stdin);//freopen("out.txt","w",stdout);      while(~scanf("%d%d%d%d",&n,&m,&x,&y))      {                    int pre=(min(m,n)+1)/2;int ans,ans1,ans2;          if(n==m&&n%2&&x==(n+1)/2&&x==y)          {              ans=pre-1;          }          else if(n==m)  ans=pre;          else          {              int up=x-1,down=n-x,left=y-1,right=m-y;              ans1=   min(max( left,right  ), min(up,down)+1 )         ;              ans2= min(  max(up,down),min(left+1,right+1) )  ;              ans=max(ans1,ans2);              ans=max(ans, pre  );          }          printf("%d\n",ans);      }    return 0;}