POJ 1905 Expanding Rods 木棍膨胀

描述

当长度为L的一根细木棍的温度升高n度，它会膨胀到新的长度L'=(1+n*C)*L，其中C是热膨胀系数。

当一根细木棍被嵌在两堵墙之间被加热，它将膨胀形成弓形的弧，而这个弓形的弦恰好是未加热前木棍的原始位置。

你的任务是计算木棍中心的偏移距离。

输入

三个非负实数：木棍初始长度（单位：毫米），温度变化（单位：度），以及材料的热膨胀系数。
保证木棍不会膨胀到超过原始长度的1.5倍。

输出

木棍中心的偏移距离（单位：毫米），保留到小数点后第三位。

样例输入

1000 100 0.0001

样例输出

61.329

直接使用求方程的方式来解题，可能由于其中出现三角函数，解决起来肯定不会那么顺手，而且很难得到一个精确的答案，但是由于弧长和弦长已定，则该圆也能确定了。但是通过画图可以看出来，由于膨胀的长度绝不会超过原长度的50%，因此膨胀圆心角不会超过180度，也不会少于0度。

此题的核心是找到高度h的表达式，然后探求与角或者圆的半径的关系，然后看是否存在某种单调性，采用二分逼近法求解近似值

想明白了后，二分求角度嘛反而不是重点了，关键是角度与弦长的单调性关系值得推敲

#include<stdio.h>#include<stdlib.h>#include<math.h>int main(){    double l, ll, rig, lef, mid, n, c;    scanf("%lf%lf%lf", &l, &n, &c);    if(l<1e-14)    {        printf("0.000\n");        return 0;    }    ll=l*(1+n*c);    lef=0.0;          //角的极小值rig=asin(1.0);    //角的极大值//由于三角函数转换，得到 h= (l/2)*tan(@/2) , 所以h只与角@有关,使用二分逼近法去求解最接近的@即可//注意，二分验证是让 ll与角@ 计算得到的 木棍原始长度l`=ll*sin@/@ 与 l 进行比较，且l`与@成反比例关系    while(rig-lef>1e-14)   //在极大值与极小值之间进行二分，这个地方精度控制太低就过不了了。精度要求很高。    {        mid=(rig+lef)/2;        if(ll*sin(mid)/mid<=l)            rig=mid;        else            lef=mid;    }    printf("%.3lf\n", l/2*tan(lef/2));    return 0;}

解法2，装载自

大致题意：

一根两端固定在两面墙上的杆 受热弯曲后变弯曲

求前后两个状态的杆的中点位置的距离

 

解题思路：

几何和二分的混合体

 

 

 

 

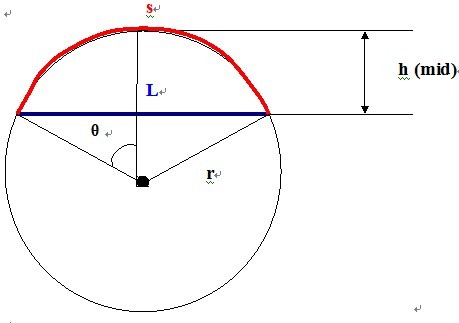
如图，蓝色为杆弯曲前，长度为L

红色为杆弯曲后，长度为s

h是所求

依题意知

S=(1+n*C)*L

 

又从图中得到三条关系式;

（1）       角度→弧度公式  θr = 1/2*s

（2）       三角函数公式  sinθ= 1/2*L/r

（3）       勾股定理  r^2 – ( r – h)^2 = (1/2*L)^2

 

把四条关系式化简可以得到

 

 

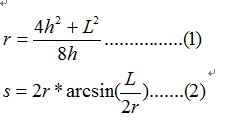
逆向思维解二元方程组：

要求（1）式的h，唯有先求r

但是由于（2）式是三角函数式，直接求r比较困难

 

因此要用顺向思维解方程组：

在h的值的范围内枚举h的值，计算出对应的r，判断这个r得到的(2)式的右边  与 左边的值S的大小关系  （ S= (1+n*C)*L ）

 

很显然的二分查找了。。。。。

那么问题只剩下 h 的范围是多少了

下界自然是0 (不弯曲)

关键确定上界

题中提及到

Input data guarantee that no rod expands by more than one half of its original length.

意即输入的数据要保证没有一条杆能够延伸超过其初始长度的一半

就是说 S max = 3/2 L

理论上把上式代入（1）(2)方程组就能求到h的最小上界，但是实际操作很困难

因此这里可以做一个范围扩展，把h的上界扩展到 1/2L  ，不难证明这个值必定大于h的最小上界，那么h的范围就为  0<=h<1/2L

这样每次利用下界low和上界high就能得到中间值mid，寻找最优的mid使得(2)式左右两边差值在精度范围之内，那么这个mid就是h

 

精度问题是必须注意的

由于数据都是double，当low无限接近high时， 若二分查找的条件为while(low<high)，会很容易陷入死循环，或者在得到要求的精度前就输出了不理想的“最优mid”

精度的处理方法参考我的程序

#include<iostream>#include<math.h>#include<iomanip>using namespace std;const double esp=1e-5;   //最低精度限制int main(void){double L,n,c,s;   //L:杆长 ，n:温度改变度 ， c:热力系数  ，s:延展后的杆长（弧长）double h;    //延展后的杆中心 到 延展前杆中心的距离double r;   //s所在圆的半径while(cin>>L>>n>>c){if(L<0 && n<0 && c<0)break;double low=0.0;    //下界double high=0.5*L; //  0 <= h < 1/2L   (1/2L并不是h的最小上界，这里做一个范围扩展是为了方便处理数据)double mid;s=(1+n*c)*L;while(high-low>esp)  //由于都是double，不能用low<high，否则会陷入死循环 {                    //必须限制low与high的精度差mid=(low+high)/2;r=(4*mid*mid+L*L)/(8*mid);if( 2*r*asin(L/(2*r)) < s )     //h偏小low=mid;else       //h偏大high=mid;}h=mid;cout<<fixed<<setprecision(3)<<h<<endl;}return 0;}

解法3

这个题有两个难点

1、解方程

图片大了点呵。。Retina屏的水果本就是不错！

这方程是超越方程，只有数值解，那怎么办呢？

2、二分单调性证明

证明如下：

上面的方程，另左边等于s，则可推得弧长s与h间关系如下：

绘制该函数图像如下：

可知该函数是随l和s单增的，故可用二分逼近。

上图是刚才那个超越方程的隐函数围道图像，也可证明。

另提供几何证明（为什么h越大s越大，可以利用二分来逼近这h在给定s下的最大值）

下面是代码：

#include <iostream>  #include <math.h>  #include <iomanip>    using namespace std;    #define eps 1e-5    int main() {      double L, n, c, s;      double h;      double r;      while (cin >> L >> n >> c) {          if (L < 0 && n < 0 && c < 0)              break;          double low = 0.0;          double high = 0.5 * L;          double mid;          s = (1 + n * c) * L;          while (high - low > eps) {              mid = (low + high) / 2;              r = (4 * mid * mid + L * L) / (8 * mid);              if (2 * r * asin(L / (2 * r)) < s)                  low = mid;              else                  high = mid;          }          h = mid;          cout << fixed << setprecision(3) << h << endl;      }  }