Codeforces Round #327 (Div. 2) C - Median Smoothing

C. Median Smoothing

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

A schoolboy named Vasya loves reading books on programming and mathematics. He has recently read an encyclopedia article that described the method of median smoothing (or median filter) and its many applications in science and engineering. Vasya liked the idea of the method very much, and he decided to try it in practice.

Applying the simplest variant of median smoothing to the sequence of numbers a1, a2, ..., an will result a new sequence b1, b2, ..., bnobtained by the following algorithm:

• b1 = a1, bn = an, that is, the first and the last number of the new sequence match the corresponding numbers of the original sequence.
• For i = 2, ..., n - 1 value bi is equal to the median of three values ai - 1, ai and ai + 1.

The median of a set of three numbers is the number that goes on the second place, when these three numbers are written in the non-decreasing order. For example, the median of the set 5, 1, 2 is number 2, and the median of set 1, 0, 1 is equal to 1.

In order to make the task easier, Vasya decided to apply the method to sequences consisting of zeros and ones only.

Having made the procedure once, Vasya looked at the resulting sequence and thought: what if I apply the algorithm to it once again, and then apply it to the next result, and so on? Vasya tried a couple of examples and found out that after some number of median smoothing algorithm applications the sequence can stop changing. We say that the sequence is stable, if it does not change when the median smoothing is applied to it.

Now Vasya wonders, whether the sequence always eventually becomes stable. He asks you to write a program that, given a sequence of zeros and ones, will determine whether it ever becomes stable. Moreover, if it ever becomes stable, then you should determine what will it look like and how many times one needs to apply the median smoothing algorithm to initial sequence in order to obtain a stable one.

Input

The first input line of the input contains a single integer n (3 ≤ n ≤ 500 000) — the length of the initial sequence.

The next line contains n integers a1, a2, ..., an (ai = 0 or ai = 1), giving the initial sequence itself.

Output

If the sequence will never become stable, print a single number  - 1.

Otherwise, first print a single integer — the minimum number of times one needs to apply the median smoothing algorithm to the initial sequence before it becomes is stable. In the second line print n numbers separated by a space  — the resulting sequence itself.

Sample test(s)

input

40 0 1 1

output

00 0 1 1

input

50 1 0 1 0

output

20 0 0 0 0

Note

In the second sample the stabilization occurs in two steps: 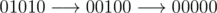, and the sequence 00000 is obviously stable.

题目要求做一种变换，使Ai = 中位数(Ai-1, Ai, Ai+1);  问要做几次这样的变换才能整个序列稳定下来，稳定后再做同样的变换序列A也不会再改变，输出变换的次数和最终得到的序列。

水题，直接上代码。思想就是把原来的串分解成n个可变换的子串，分别计算每一串变换至稳定的次数并将其处理为稳定串。最后取各子串变换次数的最大值即可，那什么情况下才能满足子串将相互不影响呢，条件就是前一个子串的end == 后一个子串的begin

#include <iostream>#include <cstdio>#include <cstring>#include <string>#include <queue>#include <algorithm>#include <map>using namespace std;const int maxn = 500000+10;int a[maxn] ;int main(){    int i,j,k,t,m,n;        cin>>n;        for(i=0;i<n;i++)        scanf("%d",&a[i]);        int begin=0, end=0;    int dis,c,res=0;    while(begin<n){        end = begin; //initializing                 while( end<n-1 && a[end]== !a[end+1])  //每次确定一个头和尾，将主串分解            end++;                dis = end - begin + 1;        c = (dis+1)/2 - 1;  //子串变换的次数        if(c>res) res = c;<span style="white-space:pre"></span>//去各子串变换的最大值

        if(dis % 2==1){   //区别处理子串中的元素为奇数和偶数的情况            for(i=begin+1;i<=end;i++){                a[i] = a[i-1];            }        }        else{            for(i=0;i<dis/2;i++){                a[begin+i] = a[begin];                a[end-i] = a[end];            }        }        begin = end+1;    }    printf("%d\n",res);    for(i=0;i<n;i++)        printf("%d ",a[i]);    return 0;}