支持向量机（二）线性可分支持向量机与硬间隔最大化

本文原创如需转载请注明出处

---

阅读目录
一.什么是函数间隔？

二.什么是几何间隔？

三.函数间隔与几何间隔的关系？

四.硬间隔最大化

五.学习的对偶算法

 

一.函数间隔

在图A，B，C三点，A离超平面是最远的，所以A被分类错误的可能性是最小的，相反C离超平面的距离是最近的，所以C被分类错误的可能性是最大的，这很好理解。那么我们就可以用“一个点距离超平面的远近”来表示分类预测的确信程度

因此我们只需要寻找一个超平面离所有边缘点都最远。

a.我们用的绝对值表示点x与超平面的距离

b.对于样本点x来说，y是它的标签（分类结果+1或者-1）

c.代表预测出来的分类结果

d.y与的乘积来代表分类的正确性及刚才提到的确信程度。这就是函数间隔。

说明：
a:以二维空间为例，直线方程为AX+BY+C=0改为+c=0。

用法向量w代替(A,B)，用特征向量x代表（x,y）,公式就是这么来的。
b：对于我们学习到的直线。把负实例点（0，0）代入，我们可以看出，算出的结果+1与它的标签-1不一致，因此线性可分支持向量机学习到的分离超平面是不准确的，也就是说当y（）>0,证明预测结果与标签一致，反之不一致。
c：进而函数间隔y（）=-1，这里的负号表示分类错误，绝对值表示点x到直线的距离，距离就是确信程度。因此说y（）来代表分类的正确性及确信程度。

1.定义函数间隔：

对于给定的训练数据集T和超平面（w,b）定义超平面（w,b）关于样本点（xi, yi）的函数间隔为：

定义超平面（w,b）关于训练数据集T的函数间隔为超平面（w,b）关于T中所有样本点（xi, yi）的函数间隔最小值

2.函数间隔的缺点：

||表示点x与超平面的距离是不准确的，因为只要成比例的改变w，b。比如改为2w，2b。超平面并没有改变，但是函数间隔却变为原来的2倍。

说明：

比如把w:（1,2）和b=1同时扩大2倍，此时把（1,1）代入方程，结果为2。代入原来的方程结果为1。但是，实际上直线的位置并没有发生改变.

因此，可以对分离超平面的法向量w加以约束，如规范化，让||w||=1，这时候函数间隔确定。这使得函数间隔成为几何间隔。

 

二.几何间隔

对于给定的训练数据集T和超平面(w，b),定义超平面(w，b)关于样本点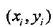的几何间隔为

定义超平面(w，b)关于训练数据集T的几何间隔为超平面(w，b)关于T中所有样本点的几何间隔之最小值，即

超平面(w，b）关于样本点的几何间隔一般是实例点到超平面的带符号的距离（signed distance),当样本点被超平面正确分类时就是实例点到超平面的距离。

三.函数间隔与几何间隔的关系

从函数间隔和几何间隔的定义可知，函数间隔和几何间隔有下面的关系：

如果||w||=1，那么函数间隔和几何间隔相等。如果超平面参数w和b成比例地改变（超平面没有改变)，函数间隔也按此比例改变，而几何间隔不变。

 

四.硬间隔最大化

如何确定线性可分超平面？

从直观上而言，超平面应该是最适合分开两类数据的。而判定“最适合”的标准就是这个超平面两边的数据的间隔最大。所以，寻找有着最大间隔的超平面。

1.间隔边缘：

注意到两个虚线是平行的，而两个虚线间的距离Gap就称为间隔（margin）为2/||w||，两个虚线称为间隔边界。

2.最大间隔分离超平面：

目标函数：  （几何间隔）

约束条件：

说明：约束条件表示每个样本点到超平面的距离至少是

考虑几何间隔与函数间隔的关系可以改写上式为

目标函数：（函数间隔除以||w||）

约束条件：

函数间隔的取值并不影响最优化问题的解，因为成比例的改变w和b目标函数和约束条件都不受到影响，所以我们可以让函数间隔为1.

 

目标函数就变为1/||w||,由于让1/||w||最大化，等价于让分母||w||最小化，为今后求导方便，把1/||w||的最大化等价为的极小化。

于是得到线性可分支持向量机学习的优化问题：

五.学习的对偶算法

拉格朗日对偶性：在约束优化问题，常常会采用拉格朗日对偶性来将原始问题转化为对偶问题，通过求解对偶问题而得到原始问题的解。这样，可以使计算简便，并且引入核函数，进而推广到非线性分类问题。

为了求解线性可分支持向量机的最优化问题，就是将它作为原始问题利用拉格朗日对偶性，求得最优解。这就是线性可分支持向量机的对偶算法。

 

说明：

 

1.原始问题

假设是定义在上的连续可微函数（因为要对它们求导），考虑约束最优化问题：

目标函数：

约束条件：

称为约束最优化问题的原始问题。

如果没有约束条件我们可以通过求导计算出最优解，这时就想办法去掉约束条件，很自然的想到拉格朗日函数（因为朗格朗日函数就是做这个的）：

引进广义拉格朗日函数（generalizedLagrange function）:

（在这里需要提一下如果约束条件是等式的话，就利用标准的朗格朗日函数）。

这里，其中是拉格朗日乘子

特别要求

 

在这里的原始问题：

那么如何求解对偶问题呢？

步骤一：

首先构造拉格朗日函数，为此对优化问题的每一个约束条件引进拉格朗日乘子：，i=1，2，…N

我们将约束条件改写为：

此时代入广义拉格朗日函数得：

步骤二：

根据拉格朗日对偶性，原始问题的对偶问题是先对上式w,b求极小值，就是分别对它们求导。

再将它们代入圈1中，此时可以推导出更简单的形式，从该形式可以引入核计法。

说明：其中第一步是原始问题，第二步是累加和展开，第三步代入公式圈2和圈3，第四步合并系数，第五步代入公式圈1，第六步展开。

步骤三：

对参数alpha做最大化操作，将对偶问题中存在的特别要求

的约束条件和圈3中的约束条件最为最大化的约束条件，我们得到经过对偶化后的简化问题如下，

其中目标函数中的尖括号是做内积。

步骤四：

将上式的目标函数（圈4）由求极大值转换成求极小值，就得到与之等价的对偶最优化问题。

步骤五：

通过对偶问题解出来的，求得原始问题的w,b

定理：设对偶最优化问题的解，则存在下标j,使得
,并可按下式求解原始最优化问题的解

现在总结一下求解过程：