非旋转式treap及可持久化

简介：

Treap，一种表现优异的BST

优势：

其较于AVL、红黑树实现简单，浅显易懂较于Splay常数小，通常用于树套BST表现远远优于Splay或许有人想说SBT，SBT我没有实现过，据说比较快但是SBT、Splay以及旋转版Treap等BST都不可以比较方便地实现‘可持久化操作’

介绍：

Treap=Tree+HeapTreap是一颗同时拥有二叉搜索树和堆性质的一颗二叉树Treap有两个关键字，在这里定义为：    1.key，满足二叉搜索树性质，即中序遍历按照key值有序    2.fix，满足堆性质，即对于任何一颗以x为根的子树，x的fix值为该子树的最值，方便后文叙述，定义为最小值为了满足期望，fix值是一个随机的权值，用来保证树高期望为logn剩下的key值则是用来维护我们想要维护的一个权值，此为一个二叉搜索树的基本要素

支持操作：

基本操作：

    1.Build【构造Treap】【O(n)】    2.Merge【合并】【O(logn)】    3.Split【拆分】【O(logn)】    4.Newnode【新建节点】【O(1)】

可支持操作：

    1.Insert【Newnode+Merge】【O(logn)】    2.Delete【Split+Split+Merge】【O(logn)】    3.Find_kth【Split+Split】【O(logn)】    4.Query【Split+Split】【O(logn)】    5.Cover【Split+Split+Merge】【O(logn)】    and more....

操作分析：

PS:如果没有看懂可以在最后看看我的代码

1.Build

    让我们先来看看笛卡尔树，笛卡尔树同样是一颗同时拥有二叉搜索树和堆性质的一颗二叉树    ---> 笛卡尔树【维基百科】    ---> 笛卡尔树【百度百科】    笛卡尔树构造是和Treap完全一样的，如果key值是有序的，那么笛卡尔树的构造是线性的，所以我们只要把Treap当作一颗笛卡尔树构造就可以了    简要讲讲笛卡尔树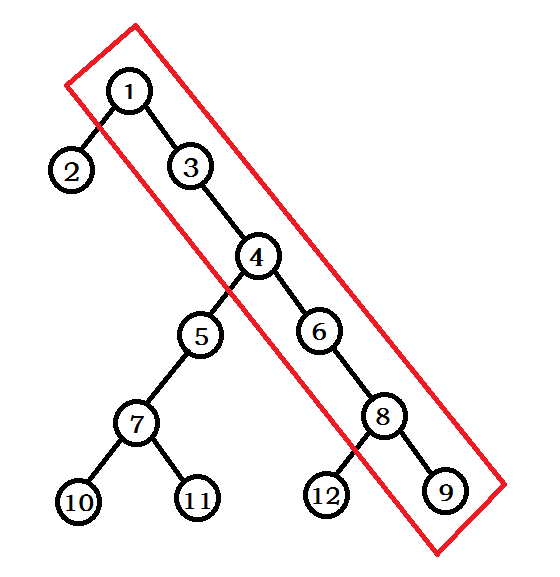：    ![这里写图片描述](http://memphis.is-programmer.com/user_files/Memphis/Image/1_20140515160140.jpg)

笛卡尔树构造时用栈维护了整棵树最右的一条链，每次在右下角处加入一个元素然后维护笛卡尔树的性质
图中，1、3、4、6、8、9为栈中元素，此时笛卡尔树满足所有性质，即在栈中元素fix值从1开始递增，假设此时我们在9的右儿子添加了一个13，若13的fix值小于栈顶元素9的fix，那么就开始退栈，停止退栈的条件有两个，满足任意一个即停止：
1.当前栈顶元素fix<13的fix【前面已经约定fix小的在上】
2.栈为空
若13的fix>3的fix并且<4的fix，那么上图会变为：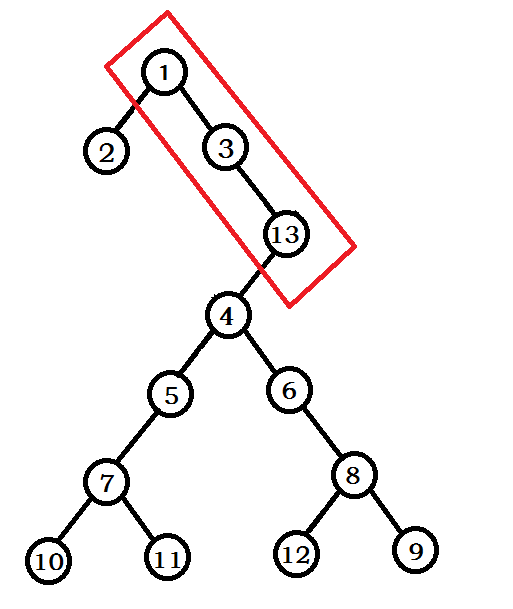

由于对于每个元素只会退栈一次，所以复杂度是O(n)

2.Merge

    对于两个相对有序的Treap【若中序遍历为递增，即TreapA的最右下角也就是最大值小于TreapB的最左下角也就是最小值】，那么Merge的复杂度是O(logn)的；    对于两个相对无序的Treap，那么Merge只能启发式合并了。    那么Merge是如何操作的？    我们可以先来看看斜堆的Merge操作：        ---> 斜堆【百度百科】        ---> 可并堆【百度文库】    非常好理解，斜堆的Merge是一个递归操作：        若当前要Merge(A,B)，若A的val < B的val，交换A,B指针；        然后A的右子树=Merge(A的右子树,B)；        最后交换一下A的左右子树．    Treap的Merge也同理，只是需要注意满足中序遍历，因此不能交换左右子树，需要自行特判，代码也很简洁

3.Split

    对于一个Treap，我们需要把它按照第K位拆分，那应该怎么做呢？    就像在寻找第K位一样走下去，一边走一边拆树，每次返回的时候拼接就可以了    由于树高是logn的，所以复杂度当然也是logn的    这样Treap有了Split和Merge操作，我们可以做到提取区间，也因此可以区间覆盖，也可以区间求和等等    除此之外因为没有了旋转操作，我们还可以进行可持久化，这个下文会讲到

4.Newnode

    这个就不说了

5.可支持操作

    一切可支持操作都可以通过以上四个基本操作完成：        Build可以用来O(n)构树还可以在替罪羊树套Treap暴力重构的时候降低一个log的复杂度        Merge和Split可用提取区间，因此可以操作一系列区间操作        Newnode单独拿出来很必要，这样在可持久化的时候会很轻松

可持久化

可持久化是对数据结构的一种操作，即保留历史信息，使得在后面可以调用之前的历史版本对于可持久化，我们可以先来看看主席树（可持久化线段树）是怎么可持久化的：    ---> 可持久化线段树【blog】由于只有父亲指向儿子的关系，所以我们可以在线段树进入修改的时候把沿途所有节点都copy一遍然后把需要修改的指向儿子的指针修改一遍就好了，因为每次都是在原途上覆盖，不会修改前一次的信息由于每次只会copy一条路径，而我们知道线段树的树高是log的，所以时空复杂度都是nlog(n)我们来看看旋转的Treap，现在应该知道为什么不能可持久化了吧？如果带旋转，那么就会破环原有的父子关系，破环原有的路径和树形态，这是可持久化无法接受的如果把Treap变为非旋转的，那么我们可以发现只要可以可持久化Merge和Split就可一完成可持久化因为上文说到了‘一切可支持操作都可以通过以上四个基本操作完成’，而Build操作只用于建造无需理会，Newnode就是用来可持久化的工具我们来观察一下Merge和Split，我们会发现它们都是由上而下的操作！因此我们完全可以参考线段树的可持久化对它进行可持久化每次需要修改一个节点，就Newnode出来继续做就可以了

Code

#include<cstdio>#include<algorithm>#include<cstring>#include<ctime>using namespace std;#define maxn 2000005#define rep(i,x,y) for(int i=x;i<=y;++i)#define dep(i,x,y) for(int i=x;i>=y;--i)struct Treap{    Treap *l,*r;    int fix,key,size;    Treap(int key_):fix(rand()),key(key_),l(NULL),r(NULL),size(1){}    inline void updata(){        size=1+(l?l->size:0)+(r?r->size:0);    }}*root;typedef pair<Treap*,Treap*> Droot;//用来Split返回两个根 inline int Size(Treap *x){return x?x->size:0;}//这样求size可以防止访问空指针 Treap *Merge(Treap *A,Treap *B){//合并操作     if(!A)return B;    if(!B)return A;    if(A->fix<B->fix){        A->r=Merge(A->r,B);        A->updata();        return A;    }else{        B->l=Merge(A,B->l);        B->updata();        return B;    }}Droot Split(Treap *x,int k){//拆分操作     if(!x)return Droot(NULL,NULL);    Droot y;    if(Size(x->l)>=k){        y=Split(x->l,k);        x->l=y.second;        x->updata();        y.second=x;    }else{        y=Split(x->r,k-Size(x->l)-1);        x->r=y.first;        x->updata();        y.first=x;    }    return y;}Treap *Build(int *a){//建造操作     static Treap *stack[maxn],*x,*last;    int p=0;    rep(i,1,a[0]){        x=new Treap(a[i]);        last=NULL;        while(p && stack[p]->fix>x->fix){            stack[p]->updata();            last=stack[p];            stack[p--]=NULL;        }        if(p) stack[p]->r=x;        x->l=last;        stack[++p]=x;    }    while(p) stack[p--]->updata();    return stack[1];}int Findkth(int k){//查找第K小     Droot x=Split(root,k-1);    Droot y=Split(x.second,1);    Treap *ans=y.first;    root=Merge(Merge(x.first,ans),y.second);    return ans->key;}int Getkth(Treap *x,int v){//询问一个数是第几大     if(!x)return 0;    return v<x->key?Getkth(x->l,v):Getkth(x->r,v)+Size(x->l)+1;}void Insert(int v){//插入操作     int k=Getkth(root,v);    Droot x=Split(root,k);    Treap *n=new Treap(v);    root=Merge(Merge(x.first,n),x.second);}void Delete(int k){//删除操作     Droot x=Split(root,k-1);    Droot y=Split(x.second,1);    root=Merge(x.first,y.second);}int a[maxn],M,x,y;int main(){    freopen("bst.in","r",stdin);    freopen("bst.out","w",stdout);    scanf("%d",a);    rep(i,1,a[0]) scanf("%d",a+i);    sort(a+1,a+1+a[0]);    root=Build(a);    scanf("%d",&M);    while(M--){        char ch=getchar();        while(ch!='Q' && ch!='A' && ch!='D') ch=getchar();        scanf("%d",&x);        if(ch=='Q') printf("%d\n",Findkth(x));        if(ch=='A') Insert(x);        if(ch=='D') Delete(x);    }}