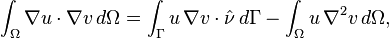integration by part in high dimension
来源:互联网 发布:淘宝虚拟试衣在哪 编辑:程序博客网 时间:2024/05/16 08:51
let's look at a question first.
how can we derive (2.10) from (2.9)?
Give the definition of integration by part in high dimension from wiki first.
{[from https://en.wikipedia.org/wiki/Integration_by_parts]
Higher dimensions[edit]
The formula for integration by parts can be extended to functions of several variables. Instead of an interval one needs to integrate over an n-dimensional set. Also, one replaces the derivative with apartial derivative.
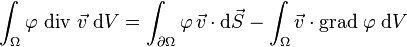 .
.
More specifically, suppose Ω is an open bounded subset of ℝn with a piecewise smooth boundary Γ. If u and v are two continuously differentiable functions on the closure of Ω, then the formula for integration by parts is
where  is the outward unit surface normal to Γ,
is the outward unit surface normal to Γ,  is its i-th component, and i ranges from 1 to n.
is its i-th component, and i ranges from 1 to n.
Replacing v in the above formula with vi and summing over i gives the vector formula
where v is a vector-valued function with components v1, ..., vn.
Setting u equal to the constant function 1 in the above formula gives the divergence theorem
For 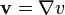 where
where 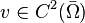 , one gets
, one gets
which is the first Green's identity.
}Then we give the relationship between the gradient and directional derivative:
{[from math guidebook for graduate entrance examination]
}
At the end, the whole derivation process will be shown:
- integration by part in high dimension
- Similarity Search in High Dimension via Hashing LSH 原始算法详解
- Siri Integration in iOS 10 with Swift – SiriKit Tutorial (Part 1)
- Display Custom Fields in a Content By Query Web Part
- Random walks in one dimension
- DRM integration in Stagefright
- Continuous Integration in DevOps
- hdu2447 K-dimension number By Assassin
- Dimension
- dimension
- Spring and Hibernate Integration Part 1
- Spring and Hibernate Integration Part 2
- Leveraging .NET Components and IDE Integration: UI AOP in an MVC use case By Daniel Cazzulino [XML MVP]
- Type 2 Dimension Logic In Informatica
- CHECK DQ Issue in Slowly Changing Dimension
- I LOVE YOU IN EVERY DIMENSION
- GENERATE DATE / TIME DIMENSION IN INFORMATICA
- NNITCN Integration team in SAPPhire
- 基于Face++实现的人脸检测(年龄检测)Android程序
- 归并排序-nlogn
- 如何居中一个浮动元素?
- 机房收费系统遇到的问题(一) datagridview一次性移除多行选中数据,同时删除数据库数据
- 玩转JavaScript正则表达式
- integration by part in high dimension
- 06 GPUImage滤镜效果
- Android 启动网络学习小笔记(未完善学到哪更到哪)
- 查看运行中Linux的内核配置选项
- 【BZOJ1015】【tyvj3487】星球大战starwar,特别的并查集技巧
- 我的C语言之路2
- Android图片缓存技术
- C
- HDU.1023 Train Problem II【大数除法、卡特兰数】--用于求出栈的n种方式(3.15)