SVM-支持向量机
来源:互联网 发布:计量型数据什么? 编辑:程序博客网 时间:2024/05/22 14:15
SVM
标签(空格分隔): ML
- SVM
- 线性SVM
- 1 为什么要大的间隔直觉
- 2 间隔的计算
- 3 解的形式转化
- 4 二次规划求解
- 5 为什么要大间隔降低模型复杂度
- 对偶SVM
- 1 非线性SVM
- 2 对偶转换
- 3 对偶形式的简化
- 4 SVM隐藏的信息
- 核型SVM
- 1 高维问题
- 2 kernel
- 3 Polynomial Kernel
- 4 Gaussian Kernel
- 5 Comparison of Kernels
- 软间隔SVM
- 1 引入软间隔-容忍误差
- 2 软间隔SVM的求解类似于硬间隔SVM
- SMO算法
- 0 SMO算法思路
- 1 2个变量二次规划的求解方法
- 11 问题形式转变
- 12 变量的约束范围
- 13 a_2的求解
- 2 变量的选择方法
- 21 第1个变量的选择
- 22 第2个变量的选择
- 23 更新b和E_i
- 3 算法流程
- 线性SVM
本文主要来源于台湾大学林轩田在Coursera的课程《机器学习技术》
1. 线性SVM
1.1 为什么要大的间隔——直觉
间隔越大能容忍越大的误差,越健壮: 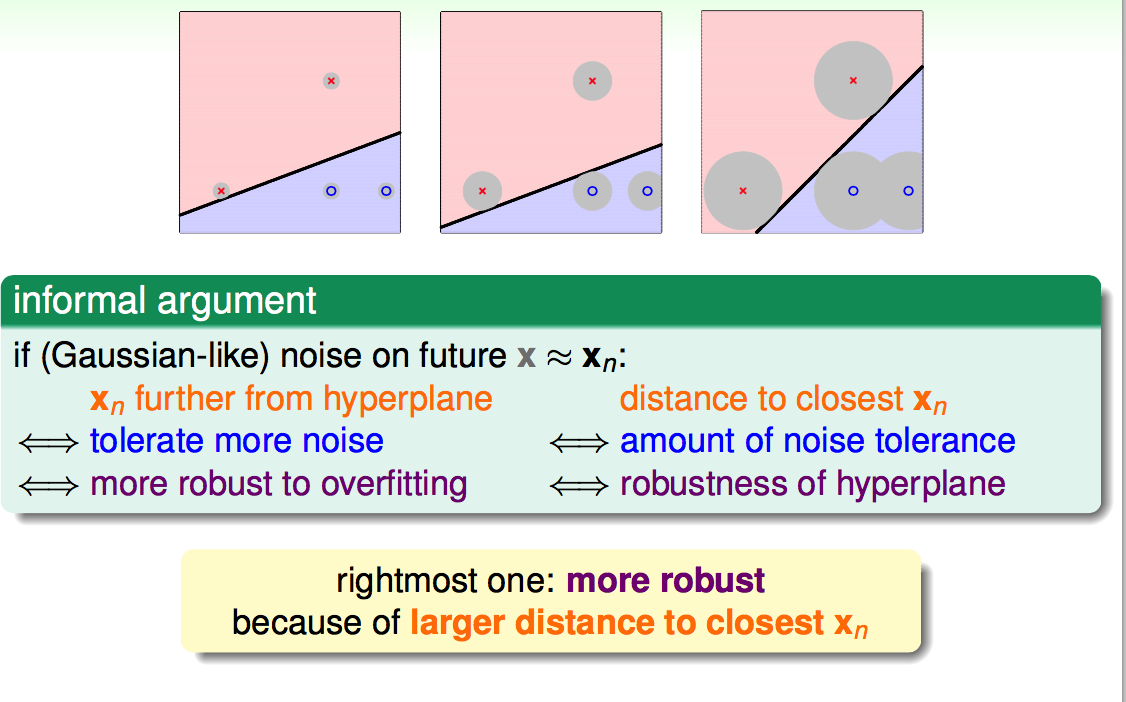
线性分类转变为: 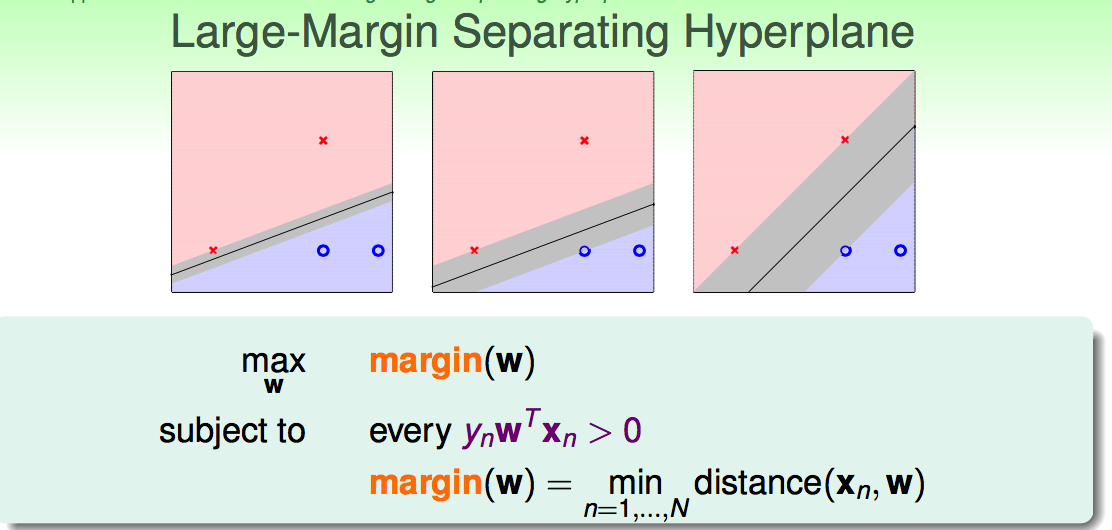
1.2 间隔的计算
向量映射: 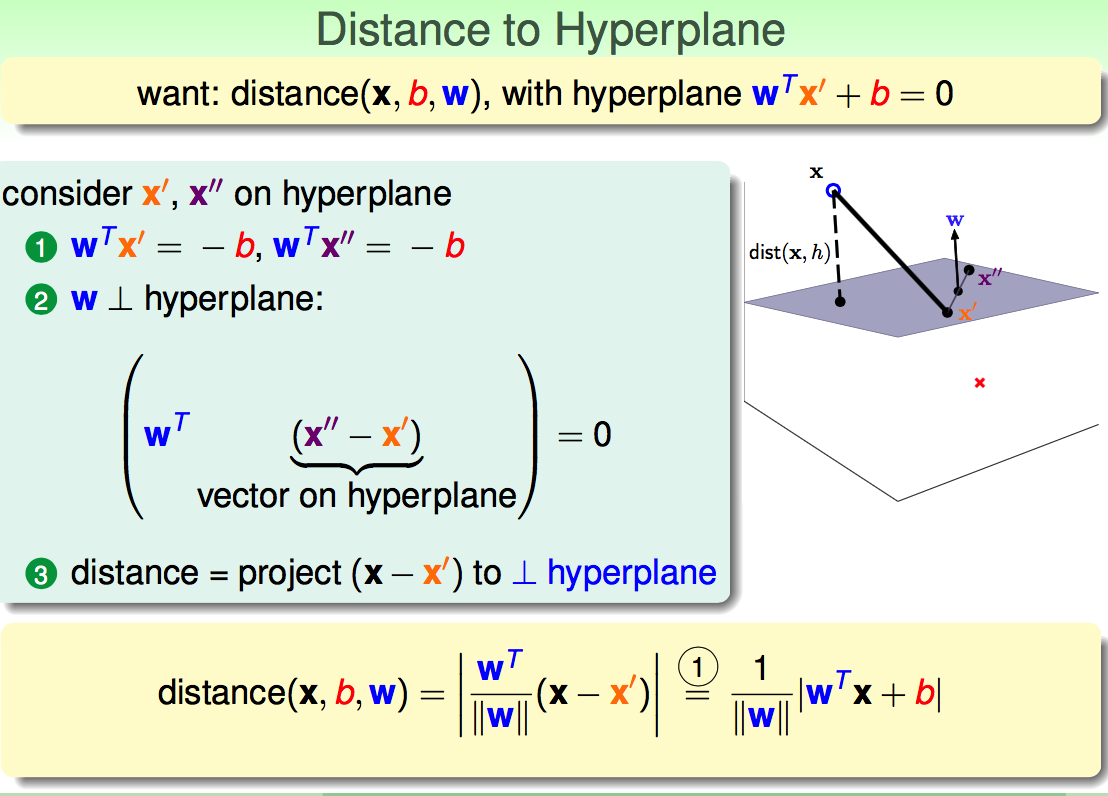
1.3 解的形式转化
(1)w和b的Scale对解没有影响,选择特定Scale的w和b,对解的形式进行化简: 
(2)对目标函数进行转换:避免根号的计算;求最大值问题,变为求最小值问题: 
1.4 二次规划求解
对于带约束的解,只能用二次规划求解: 
代入二次求解公式: 
解: 
1.5 为什么要大间隔——降低模型复杂度
(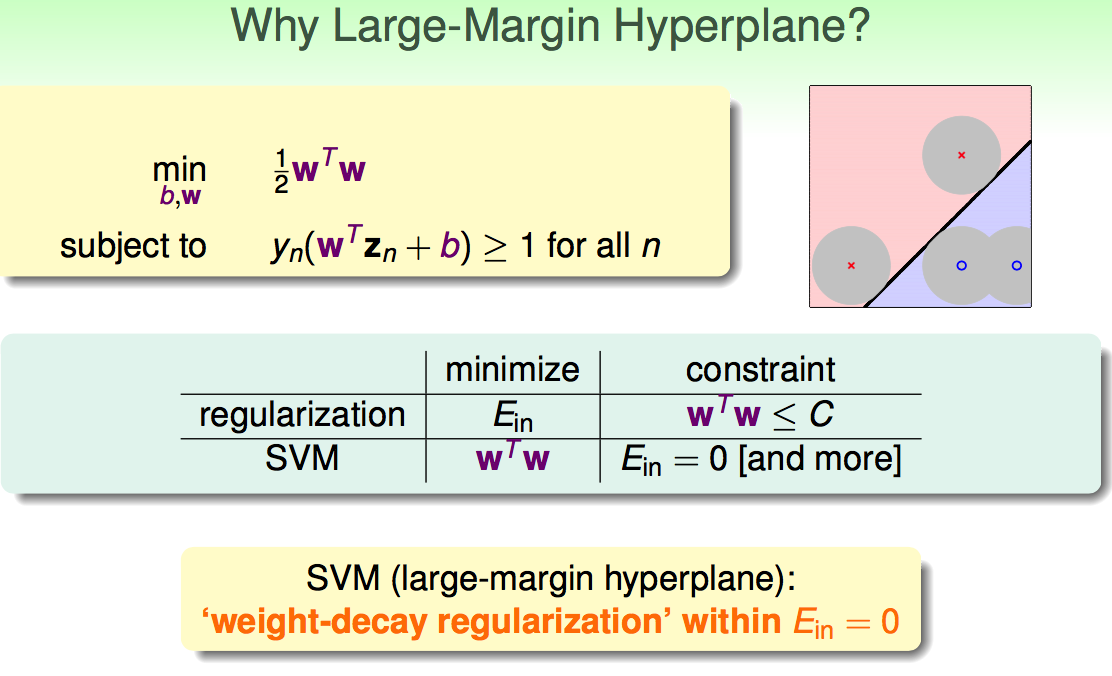

大间隔可以降低模型复杂度;特征转换可以使分类边界比较复杂: 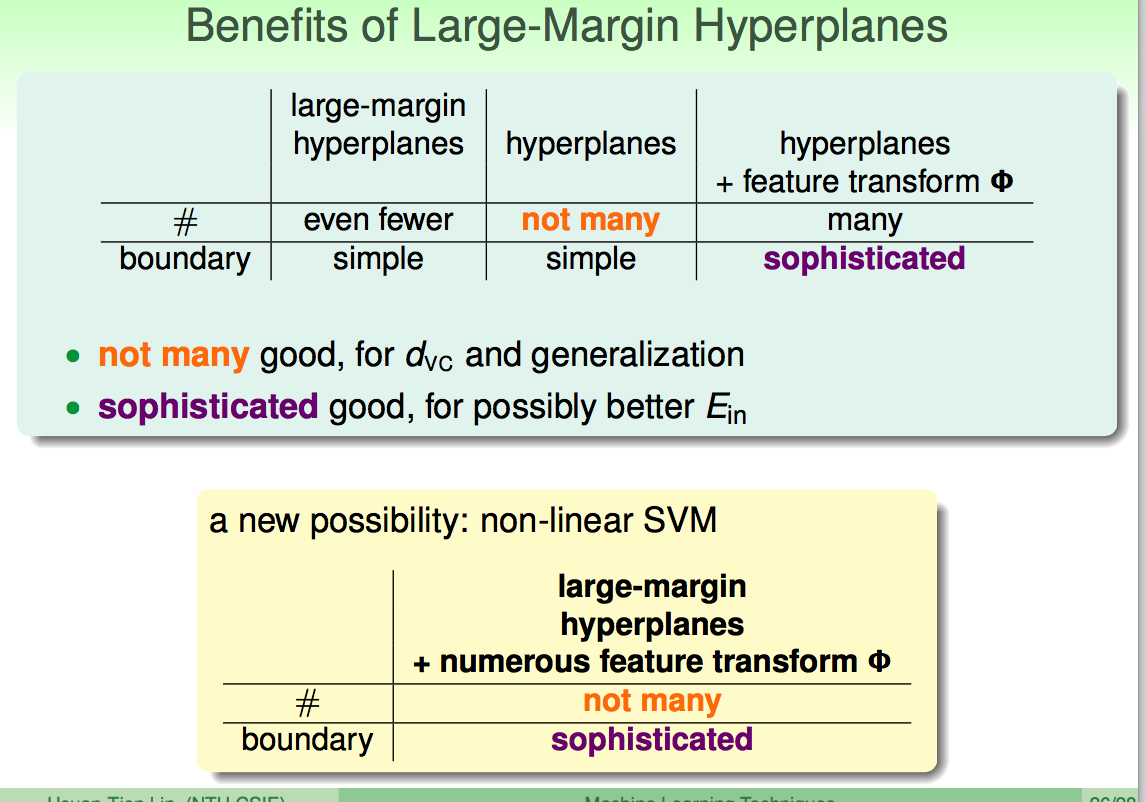
2. 对偶SVM
Solving non-linear Support Vector Machine 
2.1 非线性SVM
进行非线性转换后,维度从
2.2 对偶转换
对偶的目的在于将
等价的拉格朗日形式(去除限制条件): 
对偶形式: 
强对偶性(现在不理解。。。。) 
2.3 对偶形式的简化
通过对
通过对
KKT条件:原始问题和对偶问题的限制条件都满足,原始问题和对偶问题的内部变量的导数值均为0. 若一个变量满足KKT条件,则其为原始问题和对偶问题的最优解。 
最终的对偶形式: 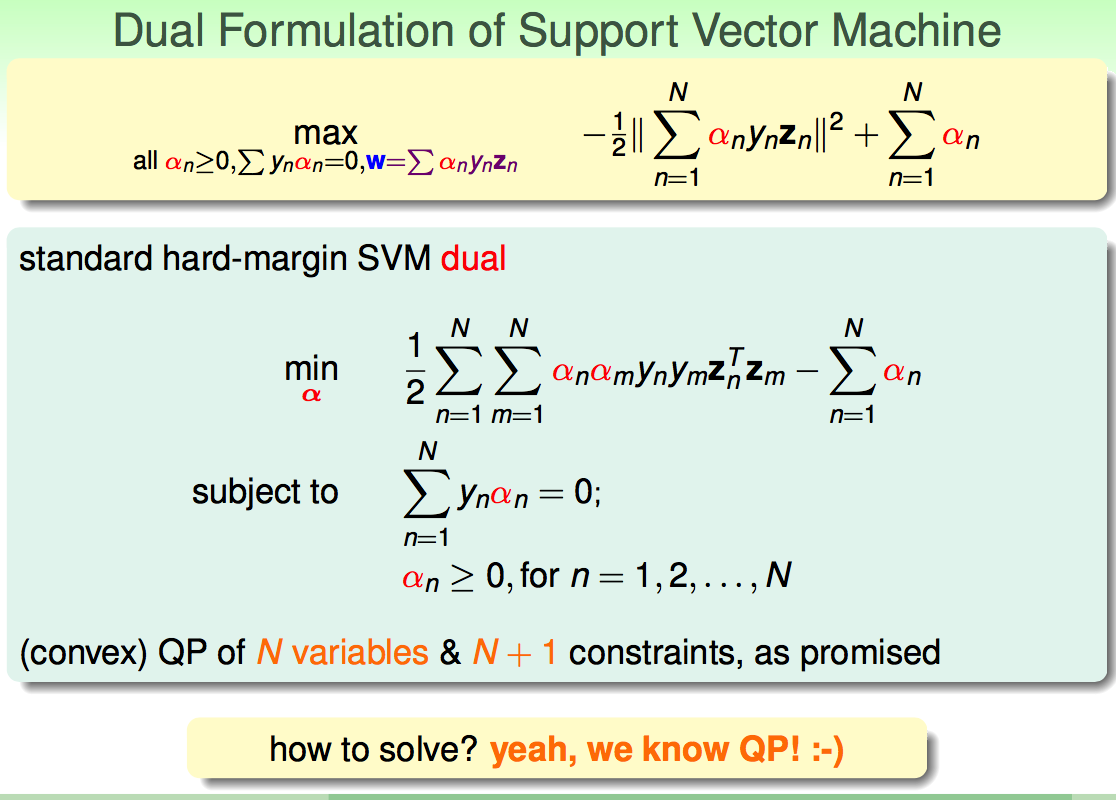
对于上述最终形式利用优化包,可求解到
求出
2.4 SVM隐藏的信息
非支持向量上的点,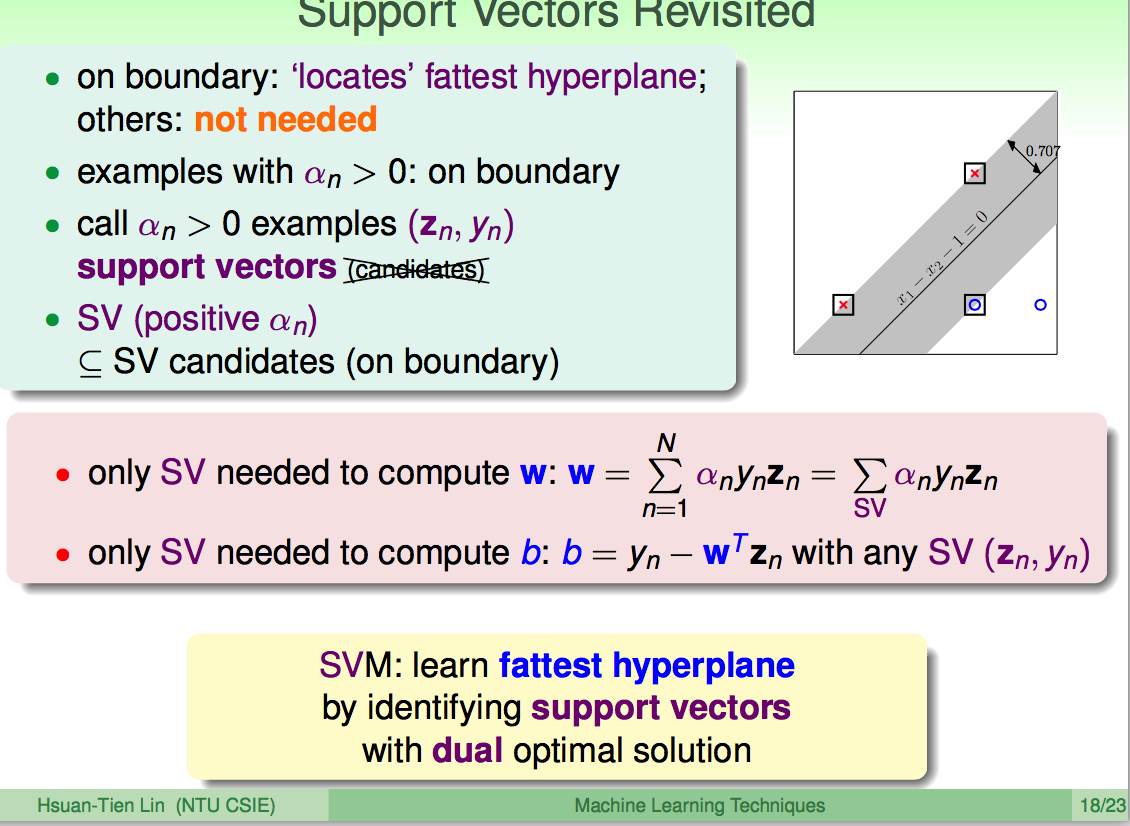
SVM与PLA(感知机)间的联系: 
3. 核型SVM
核型SVM解决高维空间计算问题。 
3.1 高维问题

3.2 kernel
Inner Product可用转换前
Kernel = Transform + Inner Product: 
Kernel SVM:所有的与高维
3.3 Polynomial Kernel
Poly-2 Kernel: 
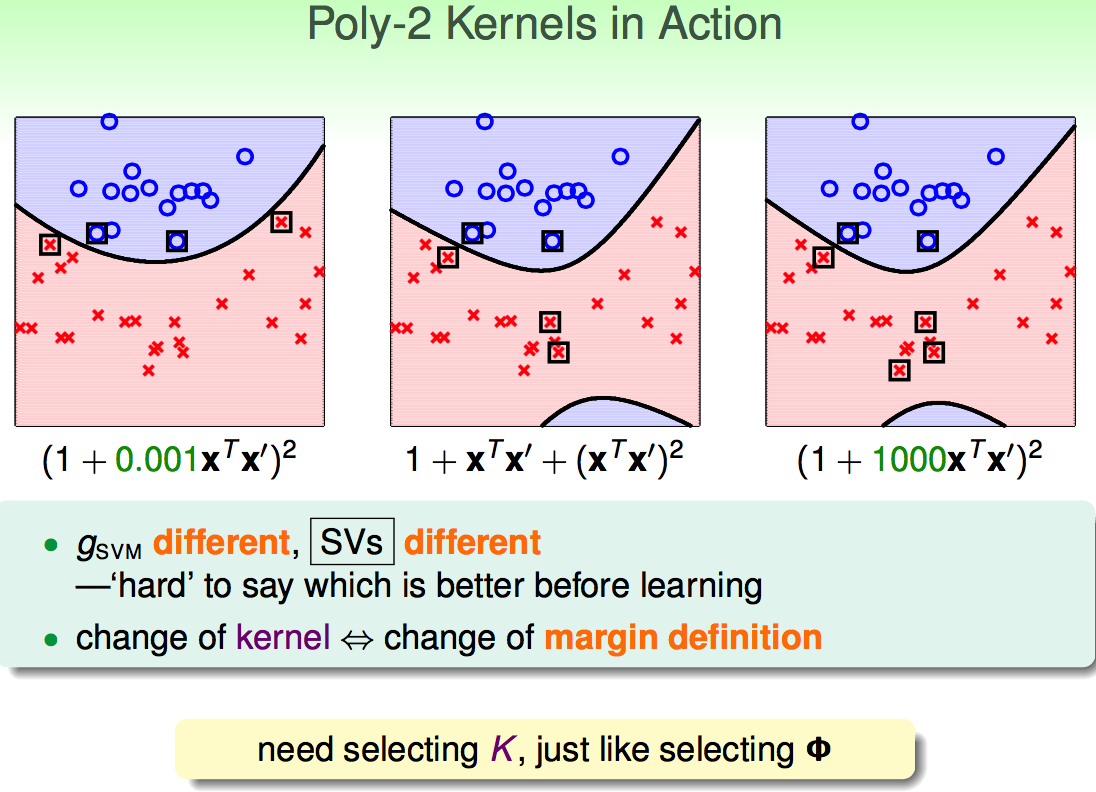
推广的多项式核: 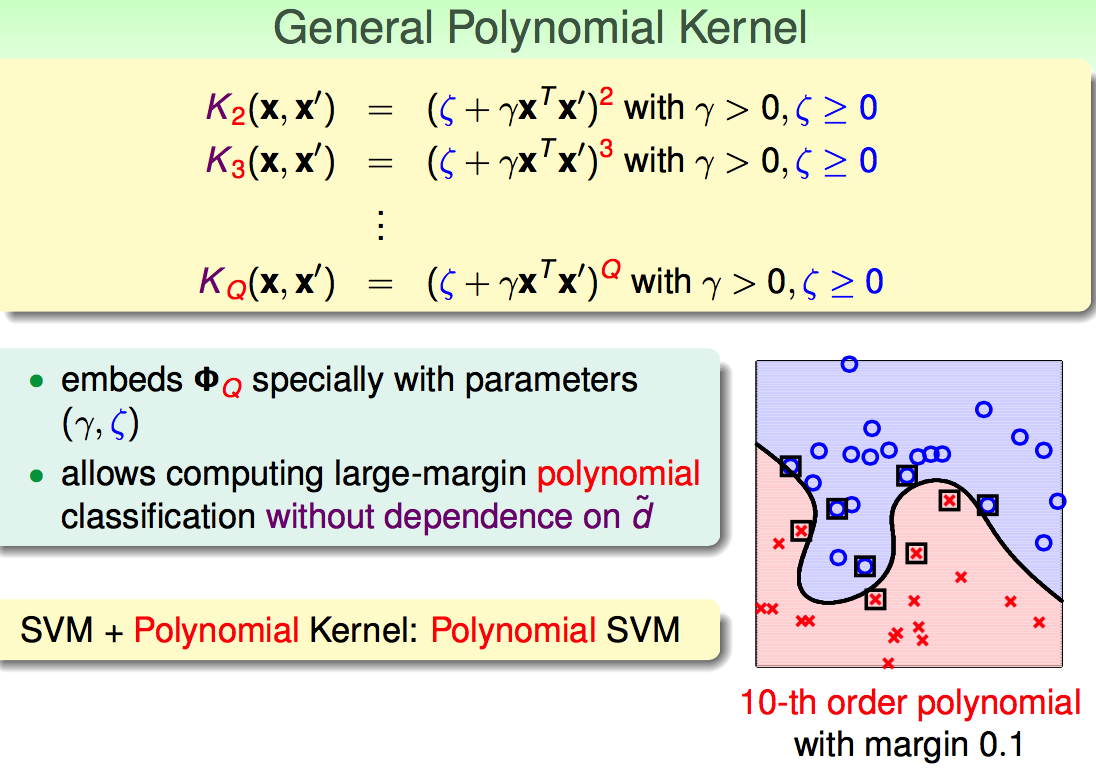
线性核: 
3.4 Gaussian Kernel
Gaussian Kernel可看作特征被转换到无限维: 
一般性的Gaussian Kernel: 
Gaussian Kernel SVM可以实现无限维的线性分隔,同时用最大间隔保持泛化能力: 
Gaussian Kernel SVM的实际使用: 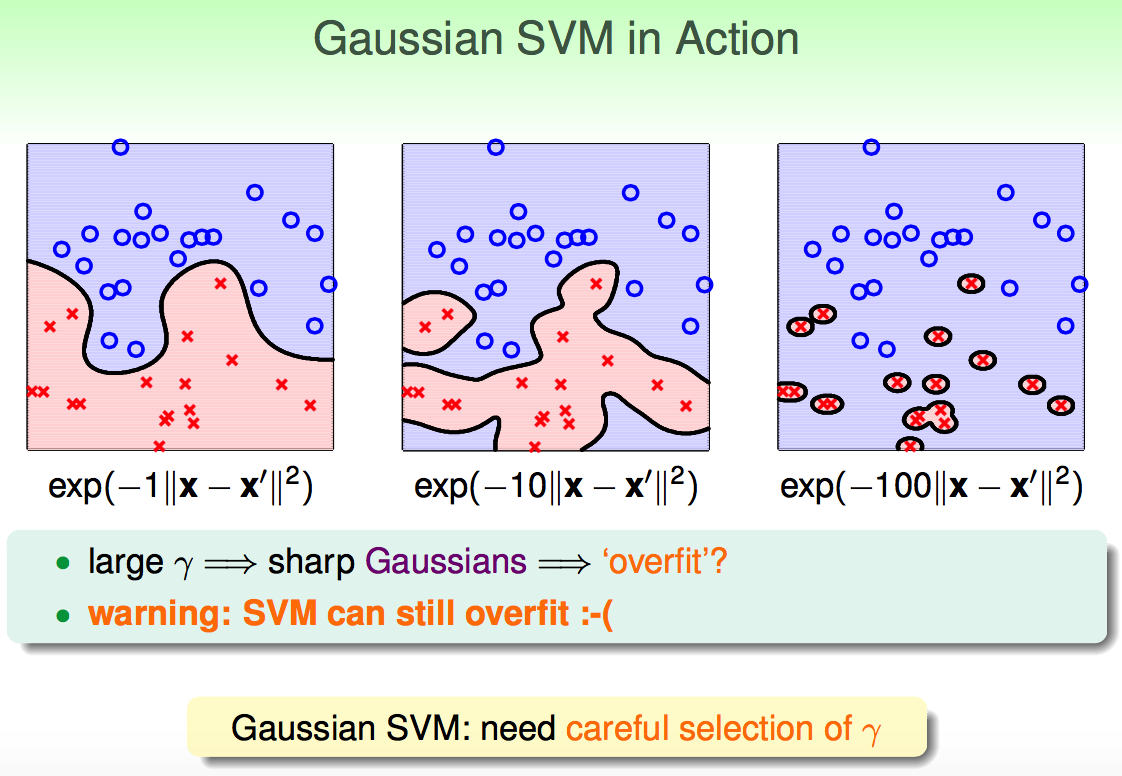
3.5. Comparison of Kernels
有效核的充分必要条件:对称和半正定 
线性核:快速和易理解,但只能用于直线分隔 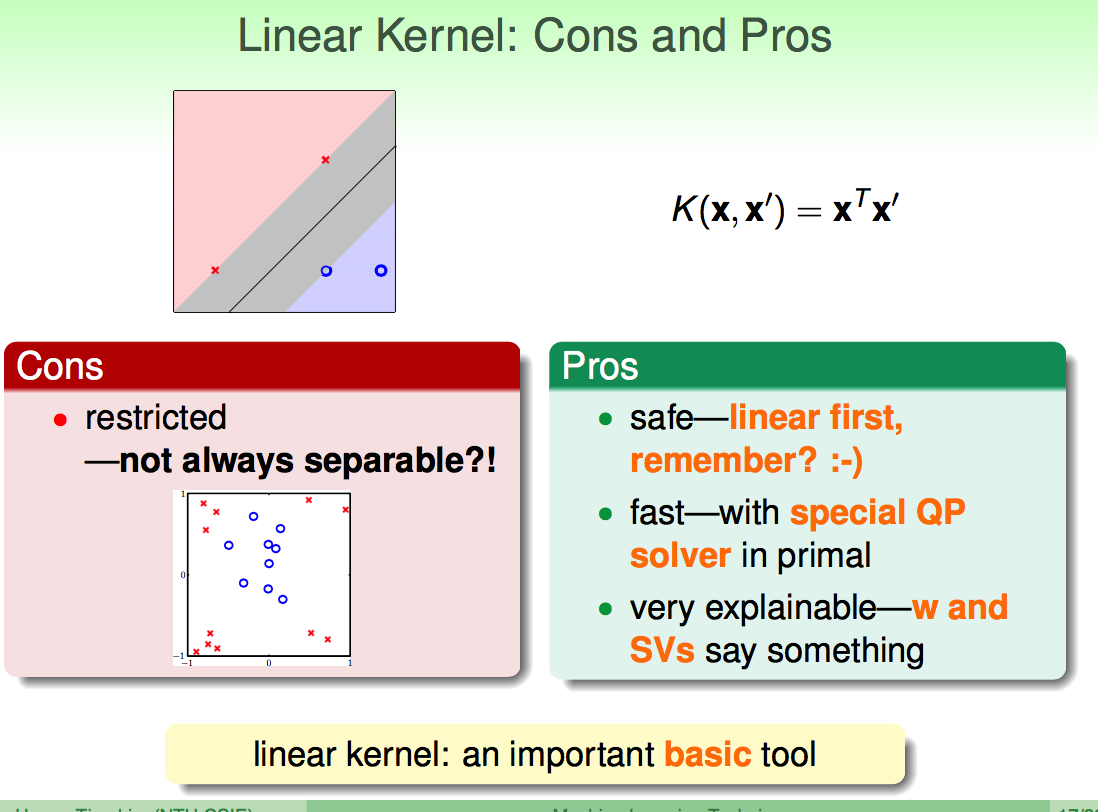
多项式核:可用于曲线分隔;但数值可能会很大,而且有3个参数,参数选取比较复杂 
高斯核:很强大,可用于各种分隔;相比多项式核,数值在一定范围内,而且只有一个参数,易于调节 
4. 软间隔SVM
4.1 引入软间隔-容忍误差
允许有一些例子被错分: 
上述的形式,不能求导,也不能区分大的误差和小的误差;因此引入软间隔SVM: 
4.2 软间隔SVM的求解(类似于硬间隔SVM)
拉格朗日对偶方程: 
对
应用与硬间隔相同的求解方法,得到如下形式: 
应用凸优化包进行求解: 

不同SV范围内的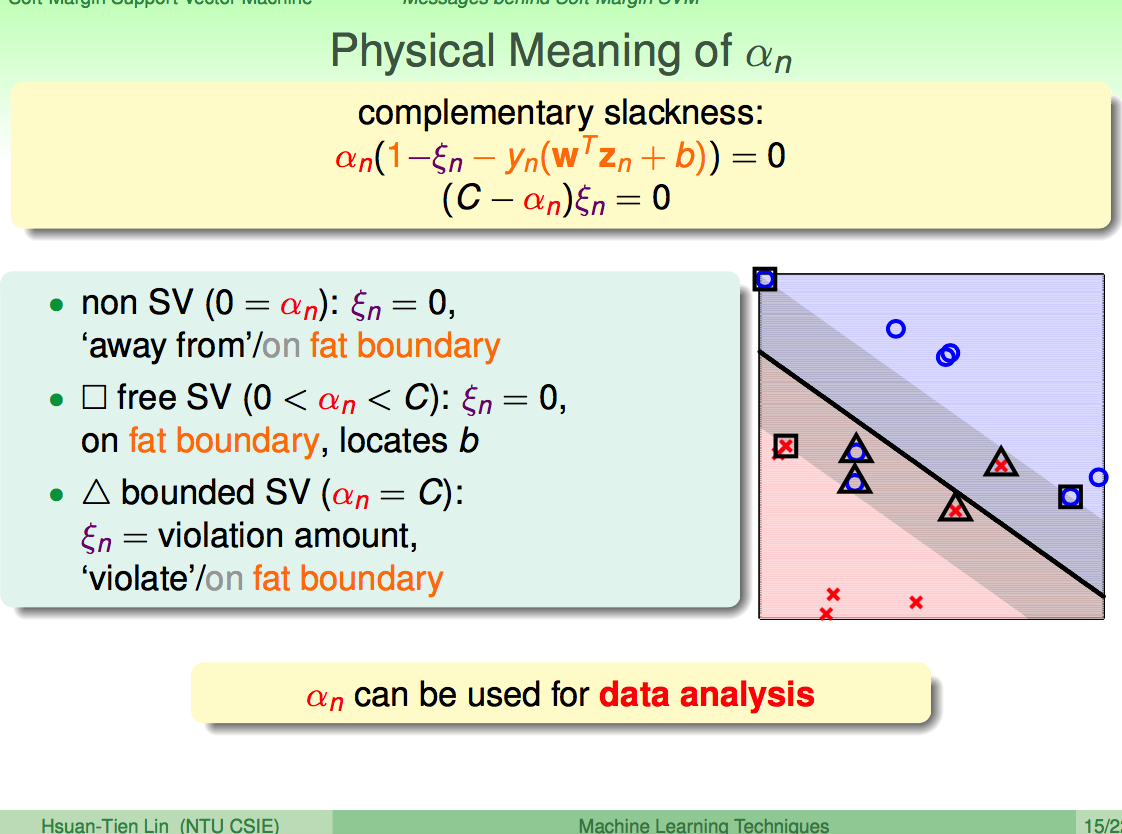
5. SMO算法
这部分内容,参考自李航的《统计学习方法》
5.0 SMO算法思路
要解决的问题: 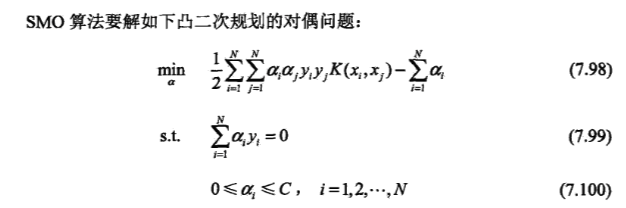
思路:选择2个变量,固定其它变量,针对这2个变量构建一个二次规划问题 

5.1 2个变量二次规划的求解方法
5.1.1 问题形式转变

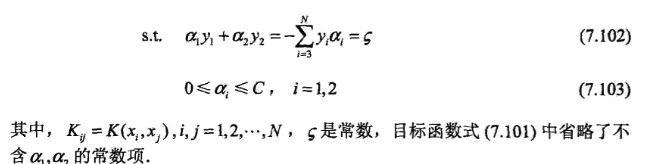
5.1.2 变量的约束范围
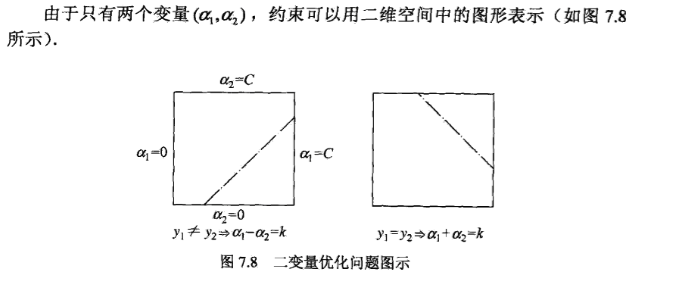

y1≠y2 :
令k=a1−a2=aold1−aold2
由0≤a1=k+a2≤C 和0≤a2≤C
可得:L=max(0,aold2−aold1) ,H=min(C+aold2−aold1,C)
同理可得:
y1=y2 :L=max(0,aold2+aold1−C) ,H=min(aold2+aold1,C)
5.1.3 a2 的求解
没有约束条件下的求解: 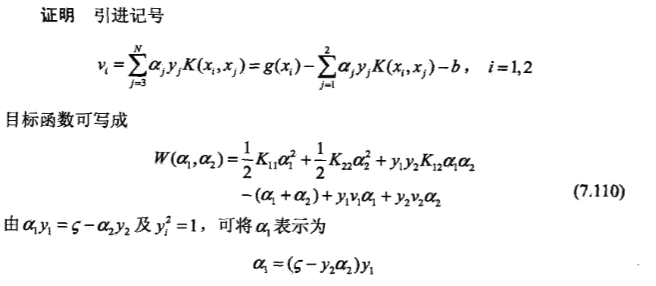

对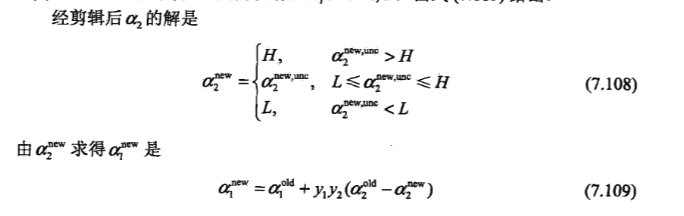
5.2 变量的选择方法
选择的2个变量,至少有一个变量是违反KKT条件的
5.2.1 第1个变量的选择

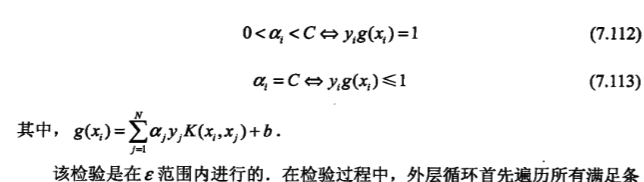
检验过程中怎样选择样本点,《统计学习方法》没有讲清楚;原文《Sequential Minimal Optimization - A Fast Algorithm for Training Support Vector Machines》是这样描述的: 
- (1) 遍历整个训练集,找一个违反KKT条件的样本点
- (2) 遍历间隔边界(
0<ai<C )上的样本点,找一个违反KKT条件的样本点
(1)和(2)构成一个寻找的循环,但对于每个循环,(2)会进行多次,直到所有间隔边界上的点都满足KKT才停止。
5.2.2 第2个变量的选择

- (1)
anew2 依赖于|E1−E2| ,E1 已知,选择a2 ,使其对应的|E1−E2| 最大 - (2)如果以上方法选择的
a2 不能使目标函数的选择有足够的下降,那么遍历在间隔边界上的点,依次讲其对应的变量作为a2 试用,直到目标函数有足够的下降。 - (3)找不到合适的
a2 ,遍历整个训练数据集 - (4)若仍找不到合适的
a2 ,则放弃第一个a1 ,再通过外层循环找另外的a1
5.2.3 更新b 和Ei
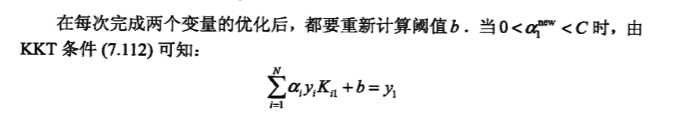

5.3 算法流程

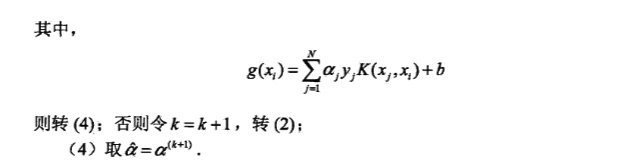
- SVM-支持向量机
- 支持向量机SVM
- SVM支持向量机
- svm支持向量机
- SVM支持向量机
- [SVM]支持向量机
- SVM 支持向量机
- 支持向量机SVM
- SVM 支持向量机
- svm支持向量机
- 支持向量机SVM
- svm支持向量机
- SVM (支持向量机)
- SVM支持向量机
- SVM支持向量机
- 支持向量机SVM
- 支持向量机(SVM)
- 支持向量机-SVM
- core i3、core m、atom x7之间的性能区别有多大 ?
- px4(apm)的log结构
- appium java 环境搭建
- 5.CSS定位、浮动
- MFC-自绘控件(CButton篇)
- SVM-支持向量机
- 在Ubuntu上安装Oracle Java 8, Java 7或者Java 6
- mysql备份与恢复详解
- Android View体系(八)从源码解析View的layout和draw流程
- opencv指令路径设置
- hdu 3954 线段树 (标记)
- Android源码解析之(七)-->LruCache缓存类
- 移动端动画设计的12个原则
- Tomcat的web服务自动跳转到https的设定


