【HDU5731 2016 Multi-University Training Contest 1I】【轮廓线DP+容斥】Solid Dominoes Tilings nm棋盘1x2多边形填充稳定方案

Solid Dominoes Tilings

Time Limit: 6000/3000 MS (Java/Others)    Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 164    Accepted Submission(s): 100

Problem Description

Dominoes are rectangular tiles with nice 2 × 1 and 1 × 2 sizes.

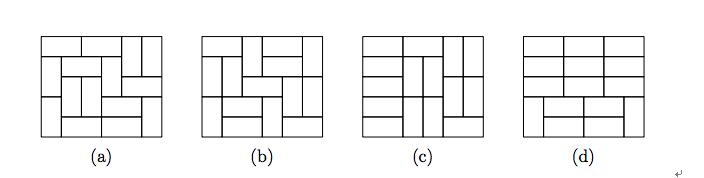
The tiling is called solid if it is not possible to split the tiled rectangle by a straight line, not crossing the interior of any tile. For example, on the picture below the tilings (a) and (b) are solid, while the tilings (c) and (d) are not.



Now the managers of the company wonder, how many different solid tilings exist for an m × n rectangle. Help them to find that out.

 

Input

The input file contains m and n(1≤m,n≤16).

 

Output

Output one integer number mod 1e9+7 - the number of solid tilings of m×n rectangle with 2 × 1 and 1 × 2 pavement tiles.

 

Sample Input

2 25 68 7

 

Sample Output

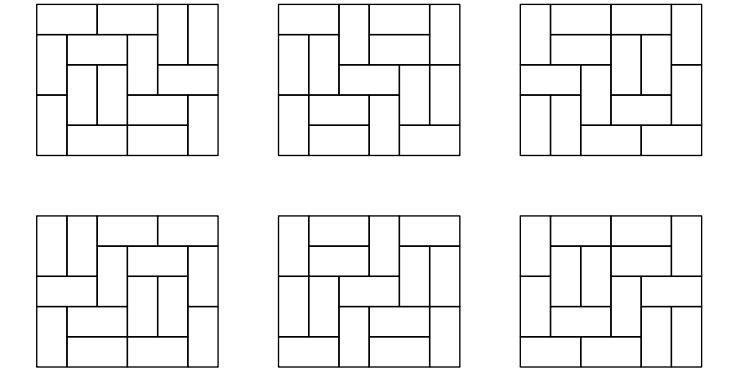
0613514
Hint
All solid tilings for the 5×6 rectangle are provided on the picture below:
 

 

Author

HIT

 

Source

2016 Multi-University Training Contest 1

#include<stdio.h>#include<iostream>#include<string.h>#include<string>#include<ctype.h>#include<math.h>#include<set>#include<map>#include<vector>#include<queue>#include<bitset>#include<algorithm>#include<time.h>using namespace std;void fre() { freopen("c://test//input.in", "r", stdin); freopen("c://test//output.out", "w", stdout); }#define MS(x,y) memset(x,y,sizeof(x))#define MC(x,y) memcpy(x,y,sizeof(x))#define MP(x,y) make_pair(x,y)#define ls o<<1#define rs o<<1|1typedef long long LL;typedef unsigned long long UL;typedef unsigned int UI;template <class T1, class T2>inline void gmax(T1 &a, T2 b) { if (b>a)a = b; }template <class T1, class T2>inline void gmin(T1 &a, T2 b) { if (b<a)a = b; }const int N = 0, M = 0, Z = 1e9 + 7, ms63 = 0x3f3f3f3f;int casenum, casei;void add(int &x, int y){if ((x += y) >= Z)x -= Z;}//基础DPint dp[2][1 << 16];int basic[17][17];//basic[i][j]表示在不考虑"稳定"的情况下，填充i*j棋盘的方案数void basicdp(){for (int m = 1; m <= 16; ++m)//枚举宽{int top = (1 << m) - 1;int now = 0, nxt = 1;MS(dp[now], 0); dp[now][top] = 1;for (int i = 0; i < m; ++i)//逐行DP{for (int j = 0; j < m; ++j)//逐列DP{MS(dp[nxt], 0);for (int sta = 0; sta <= top; ++sta){//横放if (j && !(sta & 1 << j - 1) && (sta & 1 << j)){add(dp[nxt][sta | 1 << j - 1], dp[now][sta]);}//竖放 && 不放add(dp[nxt][sta ^ 1 << j], dp[now][sta]);}swap(now, nxt);}basic[i + 1][m] = basic[m][i + 1] = dp[now][top];}}}//容斥DPint v[17];//在给定列分隔条件下的无行分割的方案计数int w[17];//在给定列分隔条件下的有行分割的方案计数int p[17];//列分隔长度int ans[17][17];void IEdp(){MS(ans, 0);for (int m = 1; m <= 16; ++m)//枚举宽{int top = (1 << m - 1) - 1;for (int sta = 0; sta <= top; ++sta)//枚举列分割状态{int num = 0;for (int i = 0; i < m - 1; ++i)if (sta >> i & 1)p[++num] = i + 1;p[++num] = m;for (int i = num; i >= 2; --i)p[i] -= p[i - 1];for (int i = 1; i <= 16; ++i)//逐行DP{LL val = 1;for (int j = 1; j <= num; ++j)val = val * basic[i][p[j]] % Z;w[i] = v[i] = val;for (int y = 1; y < i; ++y)add(v[i], Z - (LL)v[y] * w[i - y] % Z);if (num & 1)add(ans[i][m], v[i]);else add(ans[i][m], Z - v[i]);}}}//复杂度2 ^ 16（枚举列分割状态） * C（16，2）（枚举当前行和之前行） * 2（不同个宽度）//大概是3e7的复杂度，可以无压力AC。}int main(){basicdp();IEdp();int n, m;while (~scanf("%d%d", &n, &m)){printf("%d\n", ans[n][m]);}return 0;}/*【trick&&吐槽】做题多就是好。这道题为——[稳定多米诺骨牌]：http://www.51nod.com/onlineJudge/problemSolution.html#!problemId=1518同样也是——BZOJ 1435 [ZJOI2009]多米诺骨牌：【题意】给你一个n*m的棋盘，我们用1*2或2*1（即横着放或竖着放）的骨牌去填充这个棋盘。问你有多少种填法，使得这个棋盘——任意相邻两行或两列之间都必须要有一个骨牌横跨。也就是使得这个棋盘为稳定的。【类型】轮廓线DP【分析】如果没有"稳定的"这一限制，这题就变成了最基础的轮廓线DP。这道题的解题步骤是这样子的——1，基础轮廓线DP2，容斥关键是如何容斥。一开始，我所设想的容斥方法是——先通过二进制枚举哪些列是断开的，然后通过"奇减偶加"的原则，求出对于n*m的矩形，在列不分割条件下的方案数。然后再逐行枚举，做行容斥——使得矩形分成上下两块，上面一块内部无行分割，下面一块行分割任意，且上下两块都无列分割容斥减去（上方案数*下方案数）不过，这种容斥是错误的。我这样容斥掉的，是上下都无列分割的方案数。但是显然，我上下单独的一块，也许是可以有列分割的。只是在其合并之后没有了列分割。那要怎么办？我可以——先枚举行，再枚举列，然后枚举列分割的状态。在我们已知列分割状态的基础上，求出对于长为n，宽为m的图形的合法分割数——显然，该合法分割数为——对于分割的列数——奇加偶减{内部的容斥是——枚举上下两部分上部分内部无行分割下部分内部随意行分割计数相乘}这里考虑了完整的行列分割状态的影响，所以可以正确AC。至于复杂度，是有一点儿炸就是了233。【时间复杂度&&优化】O(3e7)*/