【Codeforces Round 362 (Div 2)E】【公式推导+快速幂+费马小定理】PLEASE a[i]=(1-a[i-1])除2下n次项 n为连乘数

E. PLEASE

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

As we all know Barney's job is "PLEASE" and he has not much to do at work. That's why he started playing "cups and key". In this game there are three identical cups arranged in a line from left to right. Initially key to Barney's heart is under the middle cup.

Then at one turn Barney swaps the cup in the middle with any of other two cups randomly (he choses each with equal probability), so the chosen cup becomes the middle one. Game lasts n turns and Barney independently choses a cup to swap with the middle one within each turn, and the key always remains in the cup it was at the start.

After n-th turn Barney asks a girl to guess which cup contains the key. The girl points to the middle one but Barney was distracted while making turns and doesn't know if the key is under the middle cup. That's why he asked you to tell him the probability that girl guessed right.

Number n of game turns can be extremely large, that's why Barney did not give it to you. Instead he gave you an array a₁, a₂, ..., a_ksuch that

in other words, n is multiplication of all elements of the given array.

Because of precision difficulties, Barney asked you to tell him the answer as an irreducible fraction. In other words you need to find it as a fraction p / q such that 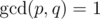, where  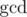is the greatest common divisor. Since p and q can be extremely large, you only need to find the remainders of dividing each of them by 10⁹ + 7.

Please note that we want 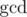 of p and q to be 1, not  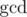of their remainders after dividing by 10⁹ + 7.

Input

The first line of input contains a single integer k (1 ≤ k ≤ 10⁵) — the number of elements in array Barney gave you.

The second line contains k integers a₁, a₂, ..., a_k (1 ≤ a_i ≤ 10¹⁸) — the elements of the array.

Output

In the only line of output print a single string x / y where x is the remainder of dividing p by 10⁹ + 7 and y is the remainder of dividing qby 10⁹ + 7.

Examples

input

12

output

1/2

input

31 1 1

output

0/1

#include<stdio.h>#include<iostream>#include<string.h>#include<string>#include<ctype.h>#include<math.h>#include<set>#include<map>#include<vector>#include<queue>#include<bitset>#include<algorithm>#include<time.h>using namespace std;void fre() { freopen("c://test//input.in", "r", stdin); freopen("c://test//output.out", "w", stdout); }#define MS(x,y) memset(x,y,sizeof(x))#define MC(x,y) memcpy(x,y,sizeof(x))#define MP(x,y) make_pair(x,y)#define ls o<<1#define rs o<<1|1typedef long long LL;typedef unsigned long long UL;typedef unsigned int UI;template <class T1, class T2>inline void gmax(T1 &a, T2 b) { if (b>a)a = b; }template <class T1, class T2>inline void gmin(T1 &a, T2 b) { if (b<a)a = b; }const int N = 0, M = 0, Z = 1e9 + 7, ms63 = 0x3f3f3f3f;int n;const int G = 2;//矩阵大小struct MX{int v[G][G];void O() { MS(v, 0); }void E() { MS(v, 0); for (int i = 0; i<G; i++)v[i][i] = 1; }MX operator * (const MX &b) const{MX c; c.O();for (int i = 0; i<G; i++){for (int j = 0; j<G; j++){for (int k = 0; k<G; k++){c.v[i][j] = (c.v[i][j] + (LL)v[i][k] * b.v[k][j]) % Z;}}}return c;}MX operator + (const MX &b) const{MX c; c.O();for (int i = 0; i<G; i++){for (int j = 0; j<G; j++){c.v[i][j] = (v[i][j] + b.v[i][j]) % Z;}}return c;}MX operator ^ (LL p) const{MX y; y.E();MX x; MC(x.v, v);while (p){if (p & 1)y = y*x;x = x*x;p >>= 1;}return y;}}a,b,c;void tryit(int p){b.O();b.v[0][0] = 4;b.v[1][0] = b.v[1][1] = 1;a.O();a.v[0][0] = 0;a.v[0][1] = 1;c = a*(b ^ (p / 2));int ans = c.v[0][0];if (p & 1)ans = (ans * 2 + 1) % Z;printf("%d", ans);}int mul(LL x, int p){LL y = 1;while (p){if (p & 1)y = y*x%Z;x = x*x%Z;p >>= 1;}return y;}void fast(int tim){int top = mul(2, tim);if (tim & 1) { top += 1; if (top >= Z)top -= Z; }else { top -= 1; if (top < 0)top += Z; }top = (LL)top * mul(3, Z - 2) % Z;printf("%d", top);}int main(){while (~scanf("%d", &n)){LL tim = 1;for (int i = 1; i <= n; ++i){LL x;scanf("%lld", &x); x %= (Z - 1);tim *= x;tim %= (Z - 1);}tim = (tim + Z - 2) % (Z - 1);//tryit(tim);//矩阵快速幂做法fast(tim);//快速幂做法printf("/");printf("%d\n", mul(2, tim));}return 0;}/*【题意】>.< 不说原题意了稍微转化一下，问题变为——a[0]=1;a[i]=(1-a[i-1])/2用分数的形式输出a[n]（分子分母先约分，再%(Z=1e9+7)）其中n以若干个数乘积的形式给出【类型】费马小定理 + （矩阵快速幂 or 快速幂）【分析】首先n这么大，我们要怎么办？可以用nlogn的快速幂做迭代，也可以通过费马小定理化简。所谓费马小定理，是说，（x^(Z-1)）%Z==1（Z为素数），即对于x的幂而言，每Z-1个就完成一次循环。于是，我们对幂做%(Z-1)的连乘，得到的tim用于之后的计算。之后要如何算你？a[i]=(1-a[i-1])/2我们找规律，是这样子的——1 0 1/2 1/4 3/8 5/16我们发现，分母一直*=2，分子是以（*2+1），（*2-1）的方式错交替性。分母为2的幂次，分子为奇数不含2，于是分母与分子其实并没有约分的必要。分母的话，快速幂可以搞定分子的话，我们可以通过矩阵快速幂搞定把（*2+1）和（*2-1）合并为（*4+1）不过我的做法有点粗暴，这道题可以直接用快速幂搞定。先要推公式——a[i]=(1-a[i-1])/2得到2a[i] = (1-a[i-1])得到2(a[i]-1/3)=-(a[i-1]-1/3)所以(a[i]-1/3)是一个以(a[0]-1/3)为首项，以(-1/2)为公比的等比数列。于是我们求出——(a[n]-1/3)=(2/3)*(-1/2)^n这样，如果n为偶数，那么结果为(1+2^(n-1))/3*2^(n-1)如果n为奇数，那么结果为(-1+2^(n-1))/3*2^(n-1)于是我们可以快速求出解来。【时间复杂度&&优化】O(n)*/