POJ 1265 pick 定理

首先来脑补一下几个几何知识

非常奇妙的证明：图形必在格点之外

从cut-the-knot上看到的。

问题：
    设想一个平面上布满间距为1的横纵直线，形成由一个个1×1正方形组成的网格。任意给一个面积小于1个单位的图形，证明这个图形总能放在网格中而不包含任何一个格点。

       

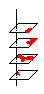
证明：
    我们可以这样考虑这个问题：把图形随意放在网格中，如何移动网格使每个格点都在图形外面。

    现在我们把给定的图形随意放在网格中。然后沿着网格线把包含有图形的网格切成1×1的小格子，从网格中拿出来。把它们重叠起来（不旋转），再想像这些格子是透明的，而图形是不透明的。从上往下看这一叠格子，你看到的会是这个图形的各部分重叠地放在一个格子中，仿佛一个沾有污渍的方块。很显然这些污渍不会布满整个方块（图形面积小于一个格子的面积），方块上总有一块干净的地方。现在我们用一颗针从一个干净的地方刺下去，把这些重起来的格子刺穿。把这些格子放回原来的网格中，你看到的会是每一个有图形的方格内都有一个针眼，这些针眼都不在图形内。现在可以把原来的网格擦掉了，这几个针眼可以看作是新网格的格点。按针眼的位置重画新的网格，那么这个图形内决不会有新网格的格点，此时，结论也就证到了。

最酷的证明：Pick定理另类证法

    难以想像，一段小小的证明竟然能比一个瘦小的留着长头发穿黑色短袖T恤紧身牛仔裤边跳边弹吉他的MM还要酷。原来一直以为这个证明已经很酷了，现在显然我已经找到了一个更酷的证明。
    Pick定理是说，假设平面上有一个顶点全在格点上的多边形P，那么其面积S(P)应该等于i+b/2-1，其中i为多边形内部所含的格点数，b是多边形边界上的格点数。绝大多数证明都是用割补的办法重新拼拆多边形。这里，我们来看一个另类的证明。
    假设整个平面是一个无穷大的铁板；在0时间，每个格点上都有一个单位的热量。经过无穷长时间的传导后，最终这些热量将以单位密度均匀地分布在整个铁板上。下面我们试着求多边形P内的热量。考虑多边形的每一条线段e：它的两个端点均在格点上，因此线段e的中点是整个平面格点的对称中心，因而流经该线段的热量收支平衡（这半边进来了多少那半边就出去了多少），即出入该线段的热量总和实际为0。我们立即看到，P的热量其实完全来自于它自身内部的i个格点（的全部热量），以及边界上的b个格点（各自在某一角度范围内传出的热量）。边界上的b个点形成了一个内角和为(b-2)*180的b边形，从这b个点流入P的热量为(b-2)*180/360 = (b-2)/2 = b/2-1。在再加上i个内部格点，于是S(P)=i+b/2-1。

Pick定理的几个出人意料的应用

   

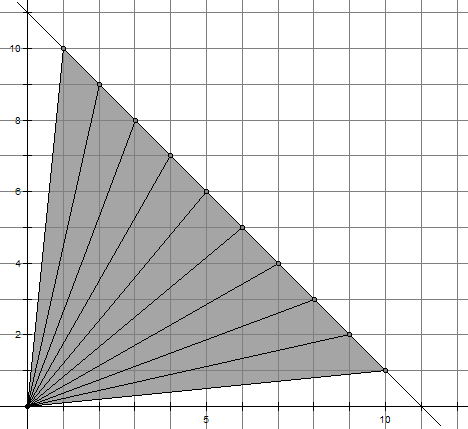
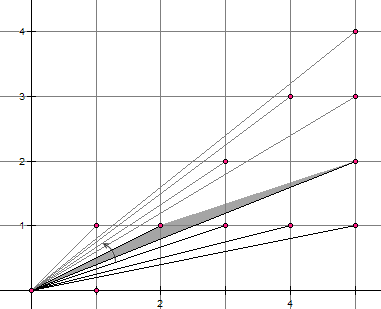
    考虑直线x+y=n，其中n是一个素数。这条直线将恰好通过第一象限里的n-1个格点（如上图，图中所示的是n=11的情况）。将这n-1个点分别和原点相连，于是得到了n-2个灰色的三角形。仔细数数每个三角形内部的格点数，你会发现一个惊人的事实：每个三角形内部所含的格点数都是一样多。这是为什么呢？

   

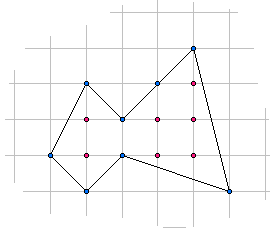
    Pick定理是说，在一个平面直角坐标系内，如果一个多边形的顶点全都在格点上，那么这个图形的面积恰好就等于边界上经过的格点数的一半加上内部所含格点数再减一。例如，上图多边形的边界上有8个格点，内部含有7个格点，那么其面积就等于8/2+7-1=10。我们曾经在这里看到过一个非常神奇非常诡异的证明。这个定理有一些非常巧妙的应用。在上面的问题里，所有三角形都是等底等高的，因此它们的面积都相等。另外，注意到x与y的和是一个素数，这表明x和y是互素的（否则x+y可以提出一个公因数d，与和为素数矛盾），也就是说(x,y)和原点的连线不会经过其它格点。既然所有三角形的面积都相等，边界上的格点数也相等，由Pick定理，我们就能直接得出每个三角形内部的格点数也相等了。

    另一个有趣的问题则是，一个n*n的正方形最多可以覆盖多少个格点？把这个正方形中规中矩地放在直角坐标系上，显然能够覆盖(n+1)^2个格点。貌似这已经是最多的了，不过如何证明呢？利用Pick定理，我们能够很快说明它的最优性。注意到由于任两个格点间最近也有一个单位的间距，再考虑到正方形的周长为4n，因此该正方形的边界上最多有4n个格点。把正方形边界上的格点数记作B，内部所含格点数记为I，于是它所能覆盖的总格点数等于I+B，由于I+B = I+B/2-1 + B/2+1 ≤ n^2 + 4n/2 + 1 = (n+1)^2，结论立即得证。

    一个东西最出神入化的运用还是见于那些与它八杆子打不着的地方。Farey序列是指把在0到1之间的所有分母不超过n的分数从小到大排列起来所形成的数列，我们把它记作F_n。例如，F_5就是

0/1, 1/5, 1/4, 1/3, 2/5, 1/2, 3/5, 2/3, 3/4, 4/5, 1/1

   

    Farey序列有一个神奇的性质：前一项的分母乘以后一项的分子，一定比前一项的分子与后一项分母之积大1。用Pick定理来证明这个结论异常简单。把分母不超过n的每一个0和1之间的分数都标在平面直角坐标系上，例如0/1就对应点(1,0)，1/5就对应点(5,1)。考虑一根从原点出发的射线由x轴正方向逆时针慢慢转动到y轴正方向，这根射线依次扫过的标记点恰好就是一个Farey序列（因为Farey序列相当于是给每个标记点的斜率排序）。考虑这根射线扫过的两个相邻的标记点，它们与原点所组成的三角形面积一定为1/2——由于分数都是最简分数，因此它们与原点的连线上没有格点；又因为这是射线扫过的两个相邻的标记点，因此三角形内部没有任何格点。另外注意到，由于三角形面积等于叉积的一半，因此两个点(m,n)和(p,q)与原点组成的三角形面积应该为(mq-np)/2。于是，对于Farey序列的两个相邻分数n/m和q/p，我们有(mq-np)/2 = 1/2，即mq-np=1。

来源：
http://www.cut-the-knot.org/ctk/PickApps.shtml
http://www.cut-the-knot.org/ctk/PickToFarey.shtml

向量叉乘

两个向量a和b的叉积写作a×b（有时也被写成a∧b，避免和字母x混淆）。向量积可以被定义为：

|向量a×向量b|=|a||b|sinθ在这里θ表示两向量之间的角夹角（0°≤θ≤180°），它位于这两个矢量所定义的平面上。

这个定义有一个问题，就是同时有两个单位向量都垂直于和：若满足垂直的条件，那么也满足。

一个简单的确定满足“右手定则”的结果向量的方向的方法是这样的：若坐标系是满足右手定则的，当右手的四指从a以不超过180度的转角转向b时，竖起的大拇指指向是c的方向。

向量积|c|=|a×b|=|a||b|sin

即c的长度在数值上等于以a，b，夹角为θ组成的平行四边形的面积。

c的方向垂直于a与b所决定的平面，c的指向按右手规则从a转向b来确定。

a×b=(aybz-azby)i+(azbx-axbz)j+(axby-aybx)k,为了帮助记忆，利用三阶行列式，写成

b×a=-a×b右手规则

三角形ABC的面积=1/2*abs(AB×AC)

Area

Time Limit: 1000MS Memory Limit: 10000KTotal Submissions: 6047 Accepted: 2685

Description

Being well known for its highly innovative products, Merck would definitely be a good target for industrial espionage. To protect its brand-new research and development facility the company has installed the latest system of surveillance robots patrolling the area. These robots move along the walls of the facility and report suspicious observations to the central security office. The only flaw in the system a competitor抯 agent could find is the fact that the robots radio their movements unencrypted. Not being able to find out more, the agent wants to use that information to calculate the exact size of the area occupied by the new facility. It is public knowledge that all the corners of the building are situated on a rectangular grid and that only straight walls are used. Figure 1 shows the course of a robot around an example area. 

 
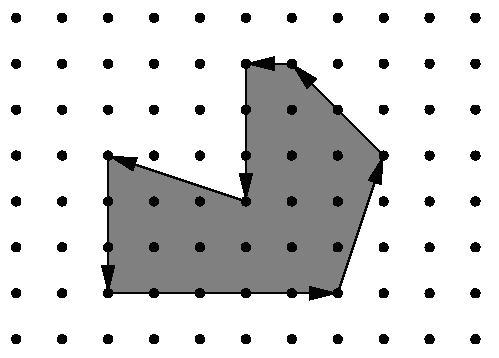
Figure 1: Example area. 

You are hired to write a program that calculates the area occupied by the new facility from the movements of a robot along its walls. You can assume that this area is a polygon with corners on a rectangular grid. However, your boss insists that you use a formula he is so proud to have found somewhere. The formula relates the number I of grid points inside the polygon, the number E of grid points on the edges, and the total area A of the polygon. Unfortunately, you have lost the sheet on which he had written down that simple formula for you, so your first task is to find the formula yourself. 

Input

The first line contains the number of scenarios. 
For each scenario, you are given the number m, 3 <= m < 100, of movements of the robot in the first line. The following m lines contain pairs 揹x dy�of integers, separated by a single blank, satisfying .-100 <= dx, dy <= 100 and (dx, dy) != (0, 0). Such a pair means that the robot moves on to a grid point dx units to the right and dy units upwards on the grid (with respect to the current position). You can assume that the curve along which the robot moves is closed and that it does not intersect or even touch itself except for the start and end points. The robot moves anti-clockwise around the building, so the area to be calculated lies to the left of the curve. It is known in advance that the whole polygon would fit into a square on the grid with a side length of 100 units. 

Output

The output for every scenario begins with a line containing 揝cenario #i:� where i is the number of the scenario starting at 1. Then print a single line containing I, E, and A, the area A rounded to one digit after the decimal point. Separate the three numbers by two single blanks. Terminate the output for the scenario with a blank line.

Sample Input

241 00 1-1 00 -175 01 3-2 2-1 00 -3-3 10 -3

Sample Output

Scenario #1:0 4 1.0Scenario #2:12 16 19.0

题意：给一个平面上的简单多边形，求边上的点，多边形内的点，多边形面积。

这个题用了很多知识点：

1、以格子点为顶点的线段，覆盖的点的个数为GCD(dx,dy)，其中，dxdy分别为线段横向占的点数和纵向占的点数。如果dx或dy为0，则覆盖的点数为dy或dx。

2、Pick公式：平面上以格子点为顶点的简单多边形的面积=边上的点数/2+内部的点数+1。

3、任意一个多边形的面积等于按顺序求相邻两个点与原点组成的向量的叉积之和。

#include <iostream>
#include <cstdio>
#include <cmath>
using namespace std;
const int N = 110;
struct node
{
    int x, y;
}p[N];
int gcd(int x,int y)
{
    return y==0?x:gcd(y,x%y);
}
int area(int a,int b)
{
    return p[a].x*p[b].y-p[a].y*p[b].x;
}


int main()
{
    int t, ncase=1;
    scanf("%d", &t);
    while(t--)
    {
        int n, dx, dy, x, y, num=0, sum=0;
        scanf("%d", &n);
        p[0].x=0, p[0].y=0;
        for(int i=1;i<=n;i++)
        {
            scanf("%d %d", &x, &y);
            p[i].x=x+p[i-1].x,p[i].y=y+p[i-1].y;
            dx=x, dy=y;
            if(x<0)
            {
                dx=-x;
            }
            if(y<0)
            {
                dy=-y;
            }
            num+=gcd(dx,dy);
            sum+=area(i-1,i);
        }
        if(sum<0)
        {
            sum=-sum;
        }
        printf("Scenario #%d:\n",ncase++);
        printf("%d %d %.1f\n\n",(sum-num+2)/2,num,sum*0.5);
    }
    return 0;
}