分形小记

前阵子被何童靴安利了一个知乎帖子：
有没有一段代码，让你觉得人类的智慧也可以璀璨无比？
图形那块美的不要不要~所以基本上一个一个瞅了瞅，所以本文算是个记录吧~

---

一、Mandelbrot分形图案

（图片来自知乎）
右侧那浑圆的大屁股，成功的引起的我的注意~
原文代码主要如下：

float x=0,y=0;int k;for(k=0;k++<256;){    float a=x*x-y*y+(i-768.0)/512;    x=a;    if(x*x+y*y>4)break;}return log(k)*47;/*作者：烧茄子链接：http://www.zhihu.com/question/30262900/answer/48741026来源：知乎著作权归作者所有，转载请联系作者获得授权。*/

代码大致是做了这件事：

用 C(Cx,Cy)代表图像上某一点，对参数x=0,y=0作出如下迭代：
x = x*x - y*y + Cx
y = 2 * x * y + Cy
直至x*x+y*y > 4 为止
然后输出迭代所需的次数作为颜色值

代码对三个通道分别作了一些不同的处理，使之更加好看了一丢丢。

刚刚看到这个迭代式其实我是懵逼的……搜了搜终于发现原来就是复数乘法 =_=……

简单而言，Mandelbrot集合是这样的：
对于复平面上的一个点c，和初始点x，对它做如下迭代：
f(x) = x^2 + c
可以得到一个迭代数列。
使这个数列收敛的所有的点，就组成了 Mandelbrot 集合。

所以终于想通了那段代码的含义了~

然后我试图轻微修改下 f(x)，看能不能得到更有趣的结果~

1. f(x) = t * x^2 + c, t为float

结果是trivial的……因为这个参数t其实就相当于这样一个变换：
t*f(x) = (t*x)^2 + t*c
也就是说，只是影响了收敛判断值，以及把c缩小了t倍。
……不贴效果图了……

2. f(x) = x^3 + c

// 迭代函数：x^3 + cvoid f_p3(float x, float y, float cx, float cy, float& x_out, float& y_out){    float new_x_out = t * (x*x*x-3*x*y*y) + cx;    float new_y_out = t * (3*x*x*y-y*y*y) + cy;    x_out = new_x_out;    y_out = new_y_out;}

这个蛮有意思的……图如下：

第一，这个大屁股变得更圆了，这真是极好的~~
第二，这个aliasing也太严重了。。。。。

3. f(x) = x^t + c, t为float

// 迭代函数：x^power + cvoid f_pn(float x, float y, float cx, float cy, float power, float& x_out, float& y_out){    float angle = atan2(y, x);    angle *= power;    float radius = x*x+y*y;    radius = sqrt(pow(radius, power));    x_out = cos(angle) * radius + cx;    y_out = sin(angle) * radius + cy;}

大多数情况下都会有一部分显得不规则，贴几种：
t=2.5 ：相对而言比较规则了~不过还是可以看到左侧部分那块还是不规则~

t=10：漂亮么~~

嗯，现在还剩下最后一个问题。。。那就是：
这种迭代的数列的收敛性。。。。是怎么控制的。。。数学分析的书里。。。也许有？（逃。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。

二、diffusion-limited aggregation模型的图案

（图片来自知乎）
写了下注释，虽然没有刚刚那个数学性那么强，但是还是挺难懂的~
个人赶脚，关键是给每个点找到一系列的发散的路径，以及路径的终止点吧~

unsigned char RD(int i,int j){#define D DIM#define M m[(x+D+(d==0)-(d==2))%D][(y+D+(d==1)-(d==3))%D]#define R rand()%D#define B m[x][y]        return(i+j)?256-(BL(i,j))/2:0;}unsigned char GR(int i,int j){    return RD(i,j);}unsigned char BL(int i,int j){    static int m[D][D],e,x,y,d,c[4],f,n; // m[D][D]代表整个画面上存储的中间数据，c[4]代表四个方向    if(i+j<1){        for(d=D*D;d;d--)        {            m[d%D][d/D]=  d%6 ? 0   :  ( rand()%2000?1:255 ) ; //建立一个静态数组 m[1024][1024]，其成员有1/2000的概率为255，否则为1；而且在6倍处永远为0        }        for(n=1;n;n++)        {            x=R;            y=R;            if(B==1) // 挑选上述生成的静态数组中，为1的那些位置            {                f=1;                for(d=0;d<4;d++) // 遍历该点的四个方向                {                    c[d]=M; // 初始化c为该方向上的点的m的数据                    f=f<c[d]?c[d]:f; // 取 f 为四个方向上的最大值                }                if(f>2) // 如果 f 曾经获得了某个方向上的数据                {                    B=f-1; // 那么该点的值 -1                }                else // 否则                {                    ++e%=4; // 选取某个方向（对于每次循环轮流选取）                    d=e;                    if(!c[e]) // 如果该方向上为 0                     {                        B=0;M=1; // 那么当前位置为 0，刚刚的方向上也置为 0                    }                }            }        }    }    return m[i][j];}

写完注释就跑好刺激~23333~
PS：刚生成的原图比网站上的图看着效果差远了……走样得不要不要的……

三、logistic 映射得到的 Feigenbaum 分岔图

先上图~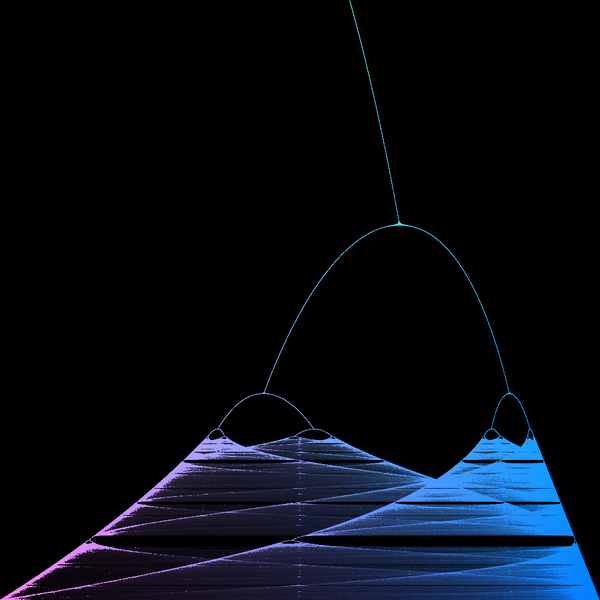

（图片来自知乎）

首先是logistic映射：

logistic映射的关键也是一个迭代数列：
x(t+1) = m * x(t) * (1 - x(t))
这个数列在m等于不同的值的时候，会有不同的收敛性，而我们要画的图，就是将m变化，然后get出它到处分布的那些点~

这里有比较详细的介绍：
Logistic映射 - 集智百科

代码如下：

unsigned char BL(int i,int j){    static float c[D][D];    if(i+j<1)    {        float a=0,b,k,r,x;        int e,o;        for(;a<D;a+=0.1) // 代表纵轴（步长间隔为 0.1，范围为 0 到 DIM）        {            for( b=0;b<D;b++) // 代表横轴            {                r=a*1.6/D+2.4; // 获得关于纵轴变化的 logistic 映射的系数                x=1.0001*b/D; // 重置下横轴的值，使之更适应于 [0,1]                for( k=0;k<D;k++) // 对横轴的值，循环DIM次，来计算 logistic 映射的收敛后的分布                {                    x=r*x*(1-x); // logistic 映射                    if(k>D) // 对于后一半的映射                    {                        e=a; // 转换为int                        o=(DM1*x); // 转换为int                        c[e][o]+=0.01; // 对于该点 ，那么把它的颜色增加一点                    }                }            }        }    }    return c[j][i]>255?255:c[j][i] * i / D; // 把颜色转换到能看的地步}

上边的 r=a*1.6/D+2.4 这部分，其实原式中只有 r 的对吧~
上边的网页里边也很清楚的说了，r将会控制这个数列的收敛性~
也就是说，这个式子里边不美观的hardcode：1.6与2.4，就是代表着对 r 的变换，亦即相当于对纵轴的缩放与平移。
不过因为r本身不能超过4（不然就不收敛了2333），所以我轻微试了几种情况：

记 r = a/D * c1 + c2
从左到右依次为：
c1=1.6, c2=2.4;
c1=2.6, c2=1.4;
c1=3.6, c2=0.4;
其实从式子上也能看出来，从左至右就是把整个图像压扁而已~

然而数学上为何会出现这种美丽的现象，对我而言依然是个谜。。。。（继续逃 ⁄(⁄ ⁄•⁄ω⁄•⁄ ⁄)⁄。。。。

---

（本文几乎完）