支持向量机

支持向量机（SVM）一

---

在看这篇文章之间，建议先看一下感知机，这样可以更好的看懂SVM。

---

---

一、最大间隔分类器

在之前的文章感知机中提到过，感知机模型对应于特征空间中将实例划分为正负两类的分离超平面，但是，感知机的解却不止一个。对同一个数据集而言，可以计算得到很多的感知机模型，不同的感知机的训练误差 都是一样的，都为0。

那么，这些训练误差都为0的感知机模型中，如何针对当前数据集，选择一个最好的感知机模型呢？现在就需要考虑模型的 泛化误差 了。即，在所有训练误差为0的感知机中，选择泛化误差最小的那个感知机，这就是SVM算法最初的目的。

基本的SVM（最大间隔分类器）是一种二分类模型，它是定义在特征空间上的间隔最大的线性分类器，间隔最大是SVM和感知机不同的地方，间隔最大化对应于泛化误差最小。

---

1.1 决策面

面对一个线性可分的二分类问题，将正负样本分开的超平面，称为决策面。

和 线性回归 模型一样，这里一般会使用一些特征函数ϕ(x)，将输入空间映射到新的特征空间中，再进行计算。

y(x)=f(wTϕ(x)+b)

这里f(⋅) 叫做激活函数，w是线性模型的系数，b一般被叫做偏置：

f(a)={+1−1a≥0a<0

这里输出的取值为 t∈{+1,−1} ，即正负样本。这里的 {+1,−1} 仅仅是一个标号，代表正负样本，并不是具体的数值。如果感觉不喜欢{+1,−1}，可以和Logistics Regression一样，使用{0,1}也行。而且，可以使用{+1,−1}主要也是因为这里是二分类问题，遇到多分类问题的时候，还得考虑其他的标号方式。

如果感觉ϕ(x)这种表述方式不太习惯，可以考虑所有的ϕ(x)=x，这样就和一般的书上的公式一致了。这种表达仅仅是我个人的喜好，式主要是为了强调，在实际问题中，输入空间x一般不会作为模型的输入，而是要将输入空间通过一定的特征转换算法ϕ(x)，转换到特征空间，最后在特征空间中做算法学习。而且，在实际问题中，各种算法基本上都是死的，但是，特征变换的这个过程ϕ(x)却是活的，很多时候，决定一个实际问题能不能很好的解决，ϕ(x)起着决定性的作用。举个简单的例子，比如Logistics Regression，数据最好要做归一化，如果数据不归一化，那么那些方差特别大的特征就会成为主特征，影响模型的计算，ϕ(x)就可以做这个事情。再或者后面要降到的核函数问题，核函数SVM能解决非线性可分问题，主要也是基于使用ϕ(x) 来做非线性特征变换。

作为一个决策面：
当样本的标号 tn=+1的时候，该样本为正样本。如果样本被正确分类，那么wTϕ(xn)+b>0，f(wTϕ(x)+b)=+1
当样本的标号 tn=−1的时候，该样本为负样本。如果样本被正确分类，那么wTϕ(xn)+b<0，f(wTϕ(x)+b)=−1

**究竟什么是决策面？
答:决策面就是能够将正负样本分开的点的集合，比如上面的模型中，决策面的数学表达式为：wTϕ(x)+b=0，决策面就是这个式子的解集，所以，一般我们就直接用这个式子代表决策面了。可以看到，对于这个决策面的数学表达式而言，w 和 b 的数值并不重要。比如，wTϕ(x)+b=0 和 2wTϕ(x)+2b=0，后一个决策面的参数数值是前一个决策面数值的两倍，但这两个决策面的解是一样的，也就是说其得到的点集是一样的，那么这两个表达式所表示的就是同一个决策面。所以，这里我要强调一点，对于一个线性决策面而言，重要的不是w 和 b 的取值，重要的是 w 和 b 的比值， w 和 b 的比值决定了一个决策面的点集，也就决定了一个决策面。**

---

1.2 最优决策面

对于线性可分的二分类问题而言，使用 感知机 算法，可以得到很多很多满足上述要求的决策面，比如下图中，就是可以将正负两类数据分开的两个决策面。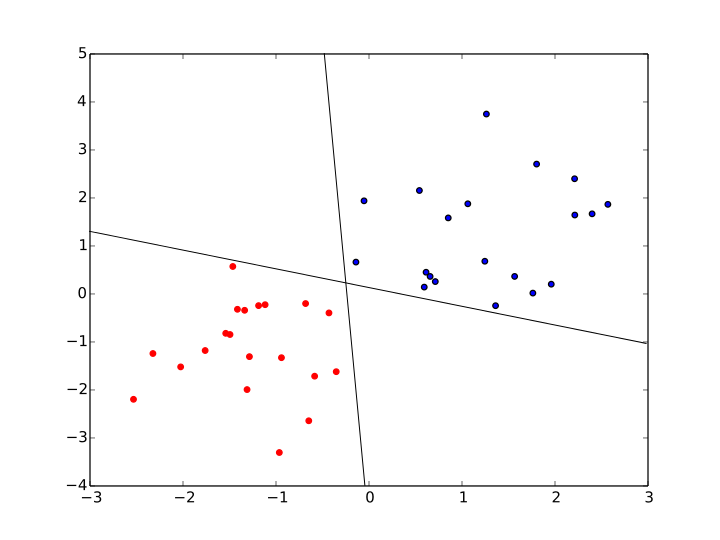

那么，在这些决策面中，哪个决策面，才是最优的决策面呢？首先，需要明确，上述的决策面，都是可以将训练样本正确分类的决策面，也就是说，上述决策面的 训练误差 都为0。要从这些训练误差都为0的模型中，选出一个最好的模型，很自然的，就需要考虑模型的 泛化误差 。

最大间隔分类器认为，决策面的泛化误差可以用训练样本集合中，离决策面最近的样本点到决策面的间隔（margin）来表示，离决策面最近的样本点，到决策面的间隔（margin）越大，那么，这个决策面的泛化误差就越小。直观的来讲，最优决策面差不多就是下面这幅图中，中间的那个决策面。

---

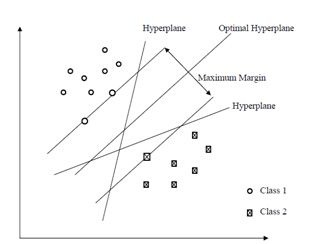
1.3 最小间隔

什么是间隔？
答：首先，要搞清楚是谁和谁的间隔，在这里指的是一个 训练样本点 和 决策面 之间的间隔。

那么，间隔又如何定义的呢？
答：间隔，就是样本点到决策面之间的距离，由中学的知识就可以知道，一个样本点 xn 到一个面 wTϕ(x)+b=0，的距离为（这里可以直接认为是点到直线的距离）：

rn=wTϕ(xn)+b||w||

但这个距离在数值上会存在正负的问题，由于样本点类别取值 tn∈{+1,−1} ，所以样本点到决策面的间隔可以改为：

rn=tn{wTϕ(xn)+b}||w||

当 tn=+1的时候，如果样本被正确分类，wTϕ(xn)+b>0，上述样本点到决策面的间隔rn 取正值
当 tn=−1的时候，如果样本被正确分类，wTϕ(xn)+b<0，上述样本点到决策面的间隔rn 仍然取正值
这样，分类正确的样本点的间隔就永远是正的了。

显然，一旦决策面有了，那么训练集合中的每个样本点 xn 到决策面都会有一间隔 rn 。自此，就可以定义样本集合到决策面最小的间隔 r 为：

r=minntn{wTϕ(xn)+b}||w||;n∈{1,2,...,N}

既然 r 是最小间隔，毫无疑问，对于任意一个样本点 xn 而言：

tn{wTϕ(xn)+b}||w||≥r

---

1.4 最小间隔最大化

前面已经说了，要使用决策面在训练样本中的最小间隔 r 来表示决策面的训练误差：最小间隔 r 越大，那么其泛化误差就越小，模型就越好。而我们这里，就是在所有可选的决策中，找出其对应的最小间隔 r 最大的那个决策面，而决策面是用参数 w 和 b 定义的，所以，最小间隔最大化可以形式化为：

argmaxw,b{minntn{wTϕ(xn)+b}||w||}

用优化理论的形式重写一下上面的式子，可以得到：

maxw,brst：ti{wTϕ(xi)+b}||w||≥r   ;i=1,2,...N

将上面的约束条件变一下型可得：

maxw,brst：ti{wTϕ(xi)+b}≥r||w||   ;i=1,2,...N

在前面已经提到过，对于一个决策面wTϕ(xi)+b=0 而言， 重要的不是w 和 b 的取值，wTϕ(x)+b=0 和 2wTϕ(x)+2b=0 的所得到的x的点集是一样的，即其决策面是一样的，这里真正重要的是w 和 b 的比值。

w 和 b 的比值，决定了一个决策面的点集，也就决定了一个决策面。

所以，只要有一个决策面，那么，唯一确定的是w 和 b 的比值，但是，w 和 b 具体的取值是可以改变的，只要w 和 b 按比例改变，决策面就是确定不变的。

也就是说，w 和 b 的比值比值不变的情况下，w是可以任意取值的。这样的话，为了便于计算，我们就取：

||w||=1r

那么，上面的式子又可以改写为：

maxw,b1||w||st：ti{wTϕ(xi)+b}≥1;i=1,2,...N

可以看到，上面的式子最大化的目标函数变成了 1/||w|| ，很容易知道，其等价于 最小化 ||w||2 ，那么最小间隔最大化，最终就可以变为下面这个最小化的约束优化问题：

minw,b||w||2st：ti{wTϕ(xi)+b}≥1;i=1,2,...N

这里，最小间隔为：

r=1||w||

在网上博客还有现有的书籍中，对于最小间隔最大化的解释，都使用了函数间隔和几何间隔的概念，我个人在第一次接触这两个概念的时候，就有些被弄糊涂了，理解了这两个概念之后，又感觉这种解释过于冗余、牵强，完全是为了解释最小间隔最大化而解释最小间隔最大化。所以，这里我直接抛弃函数间隔和几何间隔的概念，给出我个人的一种解释。

最小间隔最大化后得到的决策面，就是我们要找的泛化误差最小的决策面。对于下图中两特征的二分类问题而言，可以看出， 最小间隔为1/||w||，即，正样本到决策面的最小间隔为1/||w||；同时，负样本到决策面的最小间隔也为1/||w||。所以正负样本之间的最小间隔为2/||w||。

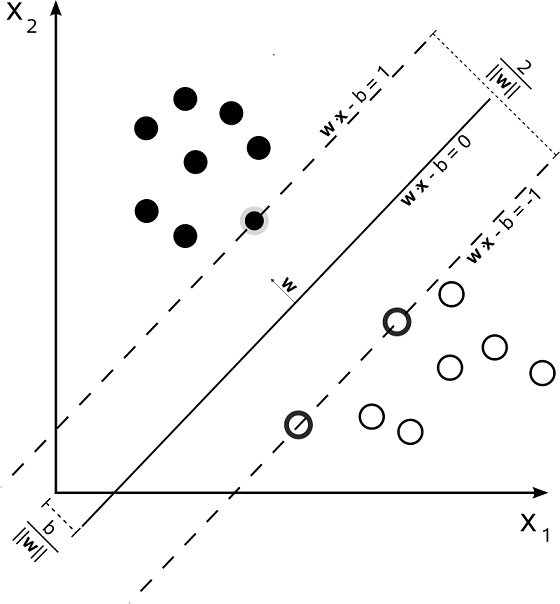
由于间隔最小的样本点 xn 满足：

tn{wTϕ(xn)+b}||w||=r=1||w||

所以，间隔最小的正样本点 xn 满足：

wTϕ(xn)+b=1

间隔最小的负样本点 xn 满足：

wTϕ(xn)+b=−1

这里定义，拥有最小间隔的正负样本点为支持向量（support vector），也就是上图中wTϕ(xn)+b=1 和 wTϕ(xn)+b=−1 所对应的那三个样本点。

关于支持向量机的名字，这里可以稍微说一下，因为这个名字并不是特别的好理解。首先是支持（support），根据柯林斯词典，support的主要意思：the activity of providing for or maintaining by supplying with money or necessities，表示的是提供一些必须品的意思。vector指的就是样本点，这个问题不大。那么问题来了，为什么将间隔最小的那些样本点叫做support vector（或者可以直接说是support point）呢？答：从图中可以看出，对于决策面而言，要想唯一的确定这个决策面，就是要根据最小的间隔r 来得到，也就是说，决策面仅仅和拥有最小间隔的那些样本点相关，和其他那些间隔大于最小间隔的样本点，是没有关系的。即：拥有最小间隔的那些样本点是决策面所必须的，而间隔大于最小间隔的样本点的有无，对决策面并不构成影响。所以将拥有最小间隔的那些样本点叫做support point， 也就是support vector。

---

1.5 拉格朗日对偶性

在求解约束最优化问题的过程中，我们常常会使用拉格朗日对偶性（Lagrange duality），把原始问题（primal problem）转换为对偶问题（dual problem）来求解，基于对偶问题的求解来得到原始问题的解。这个方法在统计学中经常使用，不仅仅本文的SVM算法用到了拉格朗日对偶性，后面要讲的最大熵模型也用到了拉格朗日对偶性。这里仅仅对拉格朗日对偶性做一个简述，我个人认为，主要知道其概念和结果即可，无需深究。拉格朗日对偶性的详细说明，可以参见Boyd的《Convex Optimization》，该书用一整个章节的篇幅来详细的论述了拉格朗日对偶性的问题。

对于一个线性规划问题，我们称之为原始问题，都有一个与之对应的线性规划问题我们称之为对偶问题。原始问题与对偶问题的解是对应的，得出一个问题的解，另一个问题的解也就得到了。并且原始问题与对偶问题在形式上存在很简单的对应关系：
- 目标函数对原始问题是极大化，对偶问题则是极小化
- 原始问题目标函数中的系数，是对偶问题约束不等式中的右端常数，而原始问题约束不等式中的右端常数，则是对偶问题中目标函数的系数
- 原始问题和对偶问题的约束不等式的符号方向相反
- 原始问题约束不等式系数矩阵转置后，即为对偶问题的约束不等式的系数矩阵
- 原始问题的约束方程数对应于对偶问题的变量数，而原始问题的变量数对应于对偶问题的约束方程数
- 对偶问题的对偶问题是原始问题

1、原始问题

假设，有f(x),ci(x),hj(x)，他们是定义在空间Rn上的连续可微的函数，也就是可导函数的意思。其约束最优化问题为：

minx∈Rnf(x)s.t.  ci(x)hj(x)≤0;i=1,2,...,k=0;j=1,2,...,l

这里ci(x)是不等式优化，而hj(x)是等式优化。

上面这种约束优化问题的形式成为原始问题。

现在，引入拉格朗日函数：

L(x,α,β)=f(x)+∑i=1kαici(x)不等式约束+∑j=1lβjhj(x)等式约束

这里 αi 和 βj 是拉格朗日乘子，且，αi≥0。也就是说，不等式约束ci(x) 的拉格朗日乘子要大于等于0，而等式约束 hj(x) 的拉格朗日乘子并没有限制。

现在考虑最大化这个拉格朗日函数，定义：

θp(x)=maxα,β;αi≥0L(x,α,β)=maxα,β;αi≥0{f(x)+∑i=1kαici(x)+∑j=1lβjhj(x)}

对于上面的最大化式子有：

• 如果不等式约束 ci(x)<0 ，等式约束 hj(x)=0 ，那么上式最大化就会使得 αi=0，βj 可以取任意值。 此时所有满足约束条件的，并且最大化结果为θp(x)=f(x)。
• 如果不等式约束 ci(x)=0 ，等式约束 hj(x)=0，那么上式最大化就会使得αi>0 ,βj 可以取任意值。此时是满足约束条件的，并且最大化结果为θp(x)=f(x)。
• 如果存在不等式约束 ci(x)>0 , 等式约束 hj(x)=0，即此时存在不等式约束违反约束条件，那么要使得上式最大化，必然会使得αi=∞ ，进而使得 θp(x)=∞。
• 如果不等式约束 ci(x)≤0 , 存在 hj(x)≠0 ，那么要使得上式最大化，必然会使得 βj=∞ ，进而使得 θp(x)=∞。

综上所述，可以知道：

θp(x)=maxα,β;αi≥0L(x,α,β)={f(x)∞ci(x)≤0 和 hj(x)=0 都满足时当存在违反ci(x)≤0 或者hj(x)=0 条件时

由于原始最优化问题就是要在满足约束条件下，求解最小化的f(x)。而由上可知，在满足约束条件的情况下，f(x)=θp(x)=maxα,β;αi≥0L(x,α,β)。

也就是说，原始约束最优化问题：

minx∈Rnf(x)s.t.  ci(x)hj(x)≤0;i=1,2,...,k=0;j=1,2,...,l

中的 f(x)，ci(x)≤0，hj(x)=0 就可以用 θp(x)=maxα,β;αi≥0L(x,α,β) 来代替。

于是乎，原始约束最优化问题就变成了一个极小极大化的问题：

minxθp(x)=minxmaxα,β;αi≥0L(x,α,β)

很显然，这个极小极大化问题，和原始问题是等价的。

为了方便，这里定义原始问题（primal problem）的最优解为：

p∗=minxθp(x)

2、对偶问题

对于一块磁铁而言，磁铁有N极和S极，N极和S极只是同一块磁铁的不同表现而已，这两个极性虽然不同，但是却拥有相同的本质：磁。他们是相辅相成的，是同一个事物的两种不同表现。就像有阴必有阳；有光明必有黑暗；而阴阳本为一体，明暗实为一物，他们都是同一个东西的不同表现而已，这个是世间万物的规律。

对偶问题和原始问题也是一样，他们是优化问题的两个不同表现形式而已，他们本质上是一个东西，只是表现的方式相反罢了。

考虑原始问题：

θp(x)=maxα,β;αi≥0L(x,α,β)

原始问题是以 α,β 为参数，以 x 为变量的极大化问题。既然对偶问题是原始问题关于优化问题的相反的表达方式，那么对偶问题就可以写成，以 α,β 为变量，以 x 为参数的极小化问题(记住一点：本质相同，表现相反):

θD(α,β)=minxL(x,α,β)

原始问题最终是被极小化，成为了一个极小极大化的问题：

minxθp(x)=minxmaxα,β;αi≥0L(x,α,β)

对偶问题，要和其相反，就需要被极大化，而称为一个极大极小化的问题：

maxα,β;αi≥0θD(α,β)=maxα,β;αi≥0minxL(x,α,β)

上面的式子，就称为拉个朗日函数的极大极小问题，并定义对偶问题（dual problem）的最优解为：

d∗=maxα,β;αi≥0θD(α,β)

由于：

θD(α,β)=minxL(x,α,β)≤L(x,α,β)≤maxα,β;αi≥0L(x,α,β)≤θp(x)

所以：

θD(α,β)≤θp(x)

上面这是式子说明，θD(α,β)的所有的解，都不大于θp(x）的解。那么，毫无疑问，对偶问题的最优解和原始问题的最优解也满足这个式子：

d∗=maxα,β;αi≥0θD(α,β)≤minxθp(x)=p∗

在我们常见的问题中，只要满足一定的条件，就可以使得d∗=p∗=L(x∗,α∗,β∗)，这里x∗,α∗,β∗ 就是最优解。这里所说的一定的条件，指的就是KKT条件。

3、KKT条件

对于原始问题 和 对偶问题而言，x∗,α∗,β∗ 分别是原始问题和对偶问题的解的充分必要条件是 x∗,α∗,β∗ 满足KKT条件：

∇xL(x∗,α∗,β∗)∇αL(x∗,α∗,β∗)∇βL(x∗,α∗,β∗)α∗ici(x∗)ci(x∗)α∗ihj(x∗)=0=0=0=0;i=1,2...k≤0;i=1,2...k≥0;i=1,2...k=0;j=1,2,...l

上述的KKT条件，看起来很吓人，其实很容易理解：函数 L(x,α,β) 是以 x,α,β 为参数的，那么其最优解 x∗,α∗,β∗ 定然满足 函数 L(x,α,β) 的梯度为0，这就是KKT条件的前三个等式：

∇xL(x∗,α∗,β∗)∇αL(x∗,α∗,β∗)∇βL(x∗,α∗,β∗)=0=0=0

前面已经说明过，函数 L(x,α,β) 要能够使用，最初的优化问题必须满足不等式约束ci(x)≤0 以及其相关的拉格朗日乘子 αi 的约束：

α∗ici(x∗)ci(x∗)α∗i=0;i=1,2...k≤0;i=1,2...k≥0;i=1,2...k

而最后一个KKT条件，对应的就是 L(x,α,β) 的等式约束:

hj(x∗)=0;j=1,2,...l

---

1.6 最小间隔最大化求解

求解最小间隔最大化，就是要求解式子：

minw,b12||w||2s.t.  ti{wTϕ(xi)+b}≥1;i=1,2,...N

而求解上面的式子，用的到方法，就是拉格朗日对偶性。这里，在原来的最小化的目标函数前面加了 1/2 ,并不会影响最后的最优解，但是对后面的公式推导相对有利，故而加上了个 1/2。

将它作为原始的优化问题，应用拉格朗日对偶性，通过求解对偶问题（dual problem）来得到原始问题（primal problem）的最优解，这个最优解，就对应于最优的决策面。

这样做的优点主要有两个：
一、对偶问题相对来说比较容易求解
二、可以很自然的引入核函数，进而推广到非线性分类器中

首先，构建拉格朗日函数，由于上面的约束优化问题中只有不等式约束，所以为所有的不等式约束添加拉格朗日乘子： αi≥0;i=1,2,...N，则拉格朗日函数为：

L(w,b,α)=12||w||2优化目标−∑i=1Nαi(ti{wTϕ(xi)+b}−1)不等式约束

根据前面关于拉格朗日对偶性的说明可以很容易知道，这个原始问题为极小极大问题：

minw,bmaxα;αi≥0L(w,b,α)

其对应的对偶问题为极大极小问题：

maxα;αi≥0minw,bL(w,b,α)

求解内部极小化

这里首先求解内部的极小化问题：

minw,bL(w,b,α)

显然，这个极小化问题是以 w,b 为参数的，那么，先使L(w,b,α) 对 w,b 求导，并令其为0：

∇wL(x,α,β)∇bL(x,α,β)=w−∑i=1Nαitiϕ(xi)=0=∑i=1Nαiti=0

那么，就有：

w=∑i=1Nαitiϕ(xi)∑i=1Nαiti=0

将 w=∑Ni=1αitiϕ(xi) 带入到 L(w,b,α) 中，就可以得到：

L=12||w||2−∑i=1Nαi(ti{wTϕ(xi)+b}−1)=12∑i=1N∑j=1N{αiαjtitj<ϕ(xi),ϕ(xj)>}−∑i=1Nαi(ti{{∑j=1Nαjtjϕ(xj)}ϕ(xi)+b}−1)=−12∑i=1N∑j=1N{αiαjtitj<ϕ(xi),ϕ(xj)>}+b∑i=1Nαiti+∑i=iNαi=−12∑i=1N∑j=1N{αiαjtitj<ϕ(xi),ϕ(xj)>}+∑i=iNαi

上面推导的导数第二步使用了：∑Ni=1αiti=0，最终可以得到：

minw,bL(w,b,α)=−12∑i=1N∑j=1N{αiαjtitj<ϕ(xi),ϕ(xj)>}+∑i=iNαi

这里的<ϕ(xi),ϕ(xj)> 是 ϕ(xi) 和 ϕ(xj) 的內积。

求解外部极大化

前面已经将内部的极小化求解得到了minw,bL(w,b,α)，这里再在其求解的结果上加上外层的极大化，那么就有下面这个约束优化问题：

maxα{−12∑i=1N∑j=1N{αiαjtitj<ϕ(xi),ϕ(xj)>}+∑i=iNαi}

s.t.  ∑i=1Nαitiαi=0≥0;i=1,2,...N

这个就是原问题的对偶问题，当然了，可以将这个对偶问题的目标函数的符号换一下，让它成为一个最小化的问题:

minα{12∑i=1N∑j=1N{αiαjtitj<ϕ(xi),ϕ(xj)>}−∑i=iNαi}

s.t.  ∑i=1Nαitiαi=0≥0;i=1,2,...N

公式推导到这个地方，就可以知道，上面这个最小化问题，就是我们最终要求解的问题，其最小化的目标函数是以 α 为参数的。

也就是说，假设最优解是 α∗=（α∗1,α∗2,...α∗N）。这里暂时不讨论如何求得这个最优解，其具体的求解算法会在后面详细的论述，现在假设，我们可以通过某种算法，将上面的这个最小化的优化问题的最优解求出来。

那么，在已知这个最优解的情况下，我们来看一下，基于这个最优解，SVM的决策面是什么样的？

根据原始问题L(w,b,α)的KKT条件可以知道：

∇wL(x∗,α∗,β∗)∇bL(x∗,α∗,β∗)α∗i(ti{w∗Tϕ(xi)+b∗}−1)ti{w∗Tϕ(xi)+b∗}−1α∗i=w∗−∑i=1Nα∗itiϕ(xi)=0=∑i=1Nα∗iti=0=0;i=1,2,...N≥0;i=1,2,...N≥0;i=1,2,...N

那么，就有：

w∗=∑i=1Nα∗itiϕ(xi)

这里，根据已经求得的 α∗i ,就可以将 w∗ 求出来了。决策面的参数有两个: w,b，w 求出来了，剩下的就是 b 了。

在前面讨论过，SVM是间隔最大化的决策面，支持向量对应的就是间隔最小的那些点，由前面关于间隔最大化的讨论可以知道，支持向量满足下面这个公式：

ti{wTϕ(xi)+b}−1=0

而根据前面对原始问题的讨论，可以知道，满足这个公式的点 xi （支持向量） ,在拉格朗日函数中，所对应的 α∗i>0 。所以，我们只需要找到一个α∗i>0 , 就可以得到 b∗:

b∗=1ti−w∗Tϕ(xi)

同时，需要注意：t2i=1，并带入w∗T，就可以将上面这个式子重写为：

b∗=ti−∑j=1Nα∗jtj<ϕ(xj),ϕ(xi)>

当然，为了稳妥起见，很多时候，我们会将所有的支持向量 xi∈S 对应的 b∗i 都求出来，然后用其均值，作为最终的 b∗。这里S 是支持向量的集合，也就是 α∗i>0 所对应的点集:

b∗=1Ns∑i=1Nsb∗i

这样，就可以求得最终的决策超平面为：

∑i=1N{α∗iti<ϕ(xi),ϕ(x)>}+b∗=0

分类决策函数可以写为：

f(x)=sign{∑i=1N{α∗iti<ϕ(xi),ϕ(x)>}+b∗}

这里就可以发现:

• 在预测的时候，w∗ 和 b∗ 仅仅依赖于训练集合中 α∗i>0 的那些样本点，而其他样本点对w∗ 和 b∗ 没有影响。但是，为了求得 w∗ 和 b∗ ，在训练阶段，还是需要整个样本集合。也就是说，在做预测的时候，支持向量机需要的内存空间是非常小的，只需要存储支持向量即可，预测过程和非支持向量无关。
• 分类决策函数仅仅依赖于输入x 和 训练样本之间的內积。这个內积是后面核函数的雏形，也是SVM得以广泛应用的关键。

---

1.7 SVM、LDA、Logistics Regression 算法比较

在之前的文章线性判别分析（Linear Discriminant Analysis）中就说过：凡是分类算法，必定有决策面，而这些分类算法所不同的是:决策面是线性的还是非线性的；以及如果得到这个决策面。

对于Logistics Regression

对于一个二分类问题，在Logistics Regression中，假设后验概率为Logistics 分布：

P(C1|x)=11+exp(wTx)P(C2|x)==exp(wTx)1+exp(wTx)

这里，使用一个单调的变换函数，logit 函数：log[p/(1−p)]，那么就可以得到：

logP(C1|x)P(C2|x)=wTx

所以Logistics Regression的决策面就是：

wTx=0

对于Linear Discriminant Analysis

这里假设fk(x)是类别Ck的类条件概率密度函数，πk 是类别Ck的先验概率，毫无疑问有∑kπk=1。根据贝叶斯理论有：

P(Ck|x)=fk(x)πk∑Kl=1fl(x)πl

LDA假设fk(x)是均值不同，方差相同的高斯分布，所以其类条件概率密度函数可以写为：

fk(x)=1(2π)p/2|Σ|1/2exp(−12(x−μk)TΣ−1(x−μk))

这里，特征x的维度为p维，类别Ck的均值为μk，所有类别的方差为Σ。

LDA和前面提到的Logistics Regression采用的单调变换函数一样，都是logit 函数：log[p/(1−p)]，对于二分类问题有：

logP(C1|x)P(C2|x)=logf1(x)f2(x)+logπ1π2=xTΣ−1(μ1−μ2)−12(μ1+μ2)TΣ−1(μ1−μ2)+logπ1π2

所以LDA的决策面就是：

xTΣ−1(μ1−μ2)−12(μ1+μ2)TΣ−1(μ1−μ2)+logπ1π2=0

显然，在LDA中，和Logistics Regression不同的是，LDA的决策面是由各个数据分布的方差和类别中心决定的。

对于SVM

对于SVM而言，我么假设，最大间隔会带来最小的泛化误差。但是，反过来思考，这个假设真的是真确的吗？在讨论LDA和Logistics Regression的时候，我们其实也是说他们的决策面是最优的。那么，到底那个算法得到的决策面才是最好的呢？

说到这个问题，让我突然想起来前段时间的一件事情，一同学面试，面试官问他：Logistics Regression对数据分布有什么要求？他并不知道怎么回答，后来回来和他们实验室的人讨论了许久，也没有结果。其实这个回答非常的简单：

我们所面对的所有的机器学算法，都是有适用范围的，或者说，我们所有的机器学习算法都是有约束的优化问题。而这些约束，就是我们在推导算法之前所做的假设。

比如：Logistics Regression，上面已经明确说明了，在Logistics Regression中，假设后验概率为Logistics 分布；再比如：LDA假设fk(x)是均值不同，方差相同的高斯分布；这些都是我们在推导算法之前所做的假设，也就是算法对数据分布的要求。

而对于SVM而言，它并没有对原始数据的分布做任何的假设，这就是SVM和LDA、Logistics Regression区别最大的地方。这表明SVM模型对数据分布的要求低，那么其适用性自然就会更广一些。如果我们事先对数据的分布没有任何的先验信息，即，不知道是什么分布，那么SVM无疑是比较好的选择。

但是，如果我们已经知道数据满足或者近似满足高斯分布，那么选择LDA得到的结果就会更准确。如果我们已经知道数据满足或者近似满足Logistics 分布，那么选择Logistics Regression就会有更好的效果。

通过这三个方法的比较，我只想说明一件事情：机器学习算法是死的，但，人是活的。使用什么机器学习算法，是根据实际问题要求，和数据的具体分布而定的。

支持向量机（SVM）二

---

• 支持向量机SVM
  • 二软间隔最大化分类器
    • 1 软间隔最大化分类器的两个问题
      • 哪些是分类错误的样本点
      • 分类错误的样本点的处理软间隔变量
    • 2 软间隔最大化分类器 的优化公式
    • 3 软间隔最大化分类器 的对偶问题
    • 4 软间隔最大化分类器 求解
    • 5 对参数 alphaxi 的讨论

---

---

二、软间隔最大化分类器

在这篇文章之前所有的讨论中，假设，所面对的数据在特征空间ϕ(x)中是线性可分的，那么，最终得到的SVM可以在输入空间X中得到一个准确的判别面，尽管其对应的判别面可能是一个非线性判别面。

然而，在现实的数据中，数据是线性不可分的（或者近似线性可分）。换一种说法就是：类条件分布存在重叠。如果这样，上面讲的算法最终只会有两种结果：1、决策面会出现严重的震荡，而无法收敛；2、即便收敛到了一个非线性的决策面，其决策面也会十分的复杂，泛化能力低。

因此，我们就需要对原始的SVM算法做一定的改动，让它对数据的要求，从线性可分扩展到线性不可分。即：允许部分训练数据存在分类错误的情况，以得到一个相对比较好的决策面。 这个改动后的SVM一般被称为软间隔最大化分类器 ，而与之相对应的，前面论述的只可以解决线性可分数据的SVM，称为 硬间隔最大化分类器 。

---

2.1 软间隔最大化分类器的两个问题

那么，现在就有两个问题摆在我们面前：

1.在SVM中，对于非线性可分的数据而言，哪些样本点是存在分类错误的样本点？
2.对于分类错误的点，软间隔最大化分类器 如何处理以得到相对比较好的决策面？

两个问题，就是软间隔最大化分类器的核心问题，回答了这两个问题，掌握了软间隔最大化分类器。

哪些是分类错误的样本点

首先必须要知道，面对一个非线性可分的数据集，哪些样本点是分类错误的样本点？可以先看下面这幅图：

图中，左边那幅图对应的是数据线性可分时，SVM的状态。此时有决策面：xTβ+β0=0 ，也就是之前讨论的 xTw+b=0 ，只是写法不同而已。根据前面“最小间隔最大化”小章节的讨论可知：最小间隔为M=1/||β||，也就是之前的表达式：r=1/||w||。这种状态，是所有数据点都分类正确，且最小间隔最大分类的状态。

图中，右边那幅图对应的就是数据线性不可分时，SVM的状态。此时决策面依然是：xTβ+β0=0，最小间隔仍然为M=1/||β||。不过，右图中ξ∗i;i=1,2...5 就是非线性可分数据在SVM中分类错误的点。

那么总结一下，在非线性可分的情况下，样本点的状态一共有下面五种：
1.非支持向量，即是在 margin 两侧，被正确分类的样本点。这些样本点对于SVM的决策面没有贡献。
2.在margin边界上面的点，这个是支持向量，且被正确分类。
3.在margin内部，被正确分类的点，比如ξ∗1,ξ∗2,ξ∗4，这些也是支持向量。
4.在决策面上的点，这些点可以拒绝判断，也可以直接认为是分类正确的点。
5.真正的被分类错误的点：ξ∗3,ξ∗5，这些点直接走到了决策面的另一边去了。

很容易发现，相对于数据线性可分的情况而言，非线性可分数据的状态多了三种情况，也就是上面五种情况的后三种，线性可分的数据只存在前面两种情况。

而后面三种情况的样本点的间隔，都比最小间隔 r 也就是图中的 M 要小一些，所以，后面这三种情况，就是SVM认为的错误的样本点（即便情况3、情况4样本被分类正确了），软间隔最大化分类器 就是要针对后面这三种情况来做文章。

---

分类错误的样本点的处理:软间隔变量

前面提到了，后面三种情况的样本点的间隔，都比最小间隔 r 也就是图中的 M 要小一些。这里首先要考虑的问题就是，如何用公式来表达后面这三种情况？这里就引入了一个最小间隔 r 的比例因子：软间隔变量 ξ。ξ是最小间隔r 的比例系数，或者叫做倍数。下面先分别讨论如何将软间隔变量 ξ 应用到上面的后三种情况中：

• 对于前面第三种情况：在margin内部，被正确分类的点，比如ξ∗1,ξ∗2,ξ∗4。这些点的间隔为：

  ξ∗i=ξi∗r;    0<ξi<1

• 对于前面第四种情况：在决策面上的点，这些点的间隔为：

  ξ∗i=ξi∗r;    ξi=1

• 对于前面第五种情况：真正的被分类错误的点：ξ∗3,ξ∗5，这些直接走到了决策面的另一边去了的点，这些点的间隔为：

  ξ∗i=ξi∗r;    ξi>1

为了将前面的第一种情况：非支持向量，即是在 margin 两侧，被正确分类的样本点。和第二种情况：在margin边界上面的点，这个是支持向量，且被正确分类。也统一的用软间隔变量ξ来表示，这里将SVM的优化公式重写为下面这个形式：

maxw,brst：ti{wTϕ(xi)+b}||w||≥r(1−ξi);  i=1,2,...Nξi≥0;i=1,2,...N

而前面第一种情况和第二种情况所对应的 ξi=0。

和“最小间隔最大化”章节中讨论的一样，w 和 b 的 比值 不变的情况下，w是可以任意取值的。这样的话，为了便于计算，我们就取：

||w||=1r

那么，上面的式子又可以改写为：

maxw,b1||w||st：ti{wTϕ(xi)+b}≥1−ξi;i=1,2,...Nξi≥0;i=1,2,...N

可以看到，上面的式子是最大化 1/||w|| ，很容易知道，其等价于 最小化 ||w||2 ，那么最小间隔最大化，最终就可以变为下面这个式子：

minw,b||w||2st：ti{wTϕ(xi)+b}≥1−ξi;i=1,2,...Nξi≥0;i=1,2,...N

这里，最小间隔为：

r=1||w||

---

2.2 软间隔最大化分类器 的优化公式

上面提到的第五种情况，真正的被分类错误的点：ξ∗3,ξ∗5，这些直接走到了决策面的另一边去了的点，所对应的ξi>1。如果说我们知道∑Ni=1ξi≤K ,那么，就可以说，这个 软间隔最大化分类器 的训练错误样本数，最多为 K个。让训练误差尽量的小也是我们的一个优化目标，这样，软间隔最大化分类器 就成了一个多目标的优化问题：

minw,b12||w||2minξ∑i=1Nξist：ti{wTϕ(xi)+b}≥1−ξi;i=1,2,...Nξi≥0;i=1,2,...N

由于上面两个优化目标的限制条件是一样的，可以将两个优化目标合成一个优化目标：

minw,b,ξ{12||w||2+C∑i=1Nξi}st：ti{wTϕ(xi)+b}≥1−ξi;i=1,2,...Nξi≥0;i=1,2,...N

这里的参数 C 是损失参数（cost parameter），用于权衡||w||2 和 ∑Ni=1ξi。一般我们将||w||2视为模型的复杂度，而将∑Ni=1ξi视为模型的错误率，损失参数C 就是在模型复杂度和模型的错误率之间找一个平衡，这个值一般作为模型的一个输入变量，需要人工设置：

• C 越小，模型越偏向于最小化||w||2，而忽略∑Ni=1ξi，这样模型非常简单，但模型的错误率相对较高。
• C 越大，模型越偏向于最小化∑Ni=1ξi，而忽略||w||2 ，这样模型的错误率相对较低，但模型相对较为复杂。

需要强调：ξi是对于SVM而言，分类错误的样本点xi 的分类错误间隔相对于最小间隔 r 的比例。我们不可能让错误的比例无限的增长，那样分类错误就太大了。所以，我们需要对错误间隔进行限制，而限制的手段，就是为总的错误间隔比例加一上限：∑ξi≤constant。这是软间隔最大化分类器 优化公式的另一种解释。

---

2.3 软间隔最大化分类器 的对偶问题

这里的步骤和 1.5 拉格朗日对偶性 几乎雷同，首先将 软间隔最大化分类器 的优化公式转换为拉个朗日函数的形式，其原始的优化公式为：

minw,b,ξ{12||w||2+C∑i=1Nξi}st：ti{wTϕ(xi)+b}≥1−ξi;i=1,2,...Nξi≥0;i=1,2,...N

拉个朗日函数为：

L(w,b,ξ,α,μ)=12||w||2+C∑i=1Nξi优化目标−∑i=1Nαi{ti{wTϕ(xi)+b}−1+ξi}−∑i=1Nμiξn不等式约束

其中，αi,μi 为拉格朗日乘子。将 L(w,b,ξ,α,μ) 分别对 w,b,ξ 求偏导:

∇wL(w,b,ξ,α,μ)∇bL(w,b,ξ,α,μ)∇ξiL(w,b,ξ,α,μ)=w−∑i=1Nαitiϕ(xi)=0=∑i=1Nαiti=0=C−αi−βi=0;i=1,2,..N

就可以得到：

w=∑i=1Nαitiϕ(xi)∑i=1Nαiti=0C−αi−βi=0;i=1,2..N

将上面三个式子带入到 L(w,b,ξ,α,μ) 中，和之前 1.6 最小间隔最大化求解 中的推导一样，最终可以得到：

minw,b,ξL(w,b,ξ,α,μ)=−12∑i=1N∑j=1N{αiαjtitj<ϕ(xi),ϕ(xj)>}+∑i=iNαi

这里的<ϕ(xi),ϕ(xj)> 是 ϕ(xi) 和 ϕ(xj) 的內积。

再对minw,b,ξL(w,b,ξ,α,μ)求极大化，即可得到软间隔最大化分类器 的对偶问题：

maxα{−12∑i=1N∑j=1N{αiαjtitj<ϕ(xi),ϕ(xj)>}+∑i=iNαi}

s.t.  ∑i=1NαitiC−αi−μiαiμi=0=0≥0≥0;i=1,2,...N

这个就是原问题的对偶问题，当然了，可以将这个对偶问题的目标函数的符号换一下,,让它成为一个最小化的问题，并将后面三个式子做一个合并:

minα{12∑i=1N∑j=1N{αiαjtitj<ϕ(xi),ϕ(xj)>}−∑i=iNαi}

s.t.  ∑i=1Nαiti0≤αi=0≤C;i=1,2,...N

这就是 软间隔最大化分类器 的对偶问题，和前面相比，这里的对偶问题只是限制条件 0≤αi≤C 和前面不同，其他的是一模一样的。

---

2.4 软间隔最大化分类器 求解

很显然，得到了软间隔最大化分类器 的对偶形式之后，其优化求解出来的就是最优解 α∗。这里再次说明：假设α∗我们已经通过某种算法得到了，至于这个算法是什么后面的章节会详细的说明，这里不同担心。

仿照 1.5 拉格朗日对偶性 中的公式推导 ，假设 x∗,α∗,ξ∗,α∗,μ∗ 为最优解，可以很容易推出 软间隔最大化分类器 拉格朗日优化的KKT条件为：

∇wL(x∗,α∗,ξ∗,α∗,μ∗)∇bL(x∗,α∗,ξ∗,α∗,μ∗)∇ξL(x∗,α∗,ξ∗,α∗,μ∗)α∗i(ti{w∗Tϕ(xi)+b∗}−1+ξ∗i)ti{w∗Tϕ(xi)+b∗}−1+ξ∗iα∗iμ∗iξ∗iξ∗iμ∗i=w∗−∑i=1Nα∗itiϕ(xi)=0=∑i=1Nα∗iti=0=C−αi−μi=0=0;i=1,2,...N≥0;i=1,2,...N≥0;i=1,2,...N=0;i=1,2,...N≥0;i=1,2,...N≥0;i=1,2,...N

在假设知道 α∗ 的情况下，由KKT条件的第一个公式：∇wL(x∗,α∗,ξ∗,α∗,μ∗)=w∗−∑Ni=1α∗itiϕ(xi)=0 可以知道，w的最优解为：

w∗=∑i=1Nα∗itiϕ(xi)

再找到一个 0<αj<C ，其所对应的样本点满足：ti{w∗Tϕ(xi)+b∗}−1=0，那么，就可以和前面的推导一样，得到：

b∗=1ti−w∗Tϕ(xi)

同时，需要注意：t2i=1，并带入w∗T，就可以将上面这个式子重写为：

b∗=ti−∑j=1Nα∗jtj<ϕ(xj),ϕ(xi)>

当然，为了稳妥起见，很多时候，我们会将所有的支持向量 xi∈S 对应的 b∗i 都求出来，然后用其均值，作为最终的 b∗。这里S 是支持向量的集合，也就是 α∗i>0 所对应的点集:

b∗=1Ns∑i=1Nsb∗i

这样，就可以求得最终的决策超平面为：

∑i=1N{α∗iti<ϕ(xi),ϕ(x)>}+b∗=0

分类决策函数可以写为：

f(x)=sign{∑i=1N{α∗iti<ϕ(xi),ϕ(x)>}+b∗}

---

2.5 对参数 α,ξ 的讨论

基于上面的推导，可以很容易的看出，软间隔最大化分类器 就是在 硬间隔最大化分类器 的基础上，处理非线性可分的数据。而参数α,ξ起着决定样本点类别的作用，那么，这里就对这两个参数做一下讨论，看看这两个参数是如何判断非线性可分数据集中的样本点的类别的。

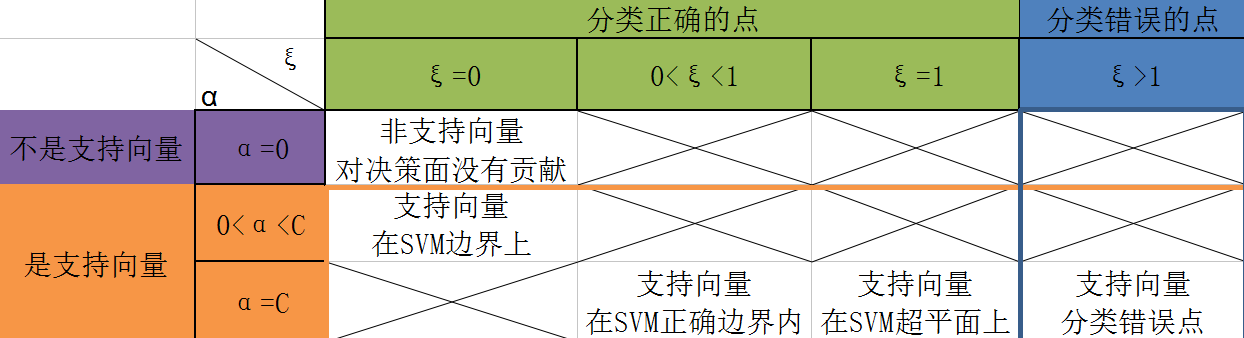
为了方便，这里直接用一张表格说明参数α,ξ 和样本点之间的关系，图种叉叉的部分，说明这种情况并不存在，下面将对这个表格做详细的说明：

在 2.1 软间隔最大化分类器的两个问题 中，就讨论过，非线性可分情况下，SVM中的样本点一共有五种情况，也就是上面表格中的所对应的五种情况。

从表格中可以粗略的观察到：
- 当αi=0 时，对应的样本点是非支持向量；当αi>0 时，对应的样本点是支持向量
- 当ξ≤1 时，对应的样本点可以被正确的分类；当ξ>1 时，对应的样本点分类错误

现在基于参数 α、ξ 对上面五种情况再做更详细的讨论：

1.当ξi=0,αi=0时，此时的样本点xi 并不是支持向量，其被完全的分类正确，样本点满足：ti{wTϕ(xi)+b}>1。
变量关系：当αi=0时，由KKT条件中的第三条：C−αi−μi=0可以知道，μi=C；再由KKT条件第七条：μ∗iξ∗i=0 可以知道：ξi=0；最后根据KKT条件的第四条和第五条，可以很容易知道：ti{wTϕ(xi)+b}>1。

2.当ξi=0,0<αi<C时,此时样本点刚好在SVM的间隔边界上，是支持向量，被正确分类，样本点满足：ti{wTϕ(xi)+b}=1。
变量关系：当0<αi<C 时，由KKT条件中的第三条：C−αi−μi=0可以知道，0<μi<C;再由KKT条件第七条：μ∗iξ∗i=0，可以知道：ξi=0。最后根据KKT条件的第四条和第五条，可以很容易知道：ti{wTϕ(xi)+b}=1。

3.当0<ξi<1,αi=C时，此时样本点在SVM的正确的间隔边界内，是支持向量，被正确分类，样本点满足：0<ti{wTϕ(xi)+b}<1。
变量关系：当αi=C时，由KKT条件中的第三条：C−αi−μi=0可以知道，μi=0;再由KKT条件第六、七条：ξ∗i≥0；μ∗iξ∗i=0，可以知道：ξi>0。根据KKT条件的第四条和第五条，可以很容易知道：ti{wTϕ(xi)+b}=1−ξi。那么，此时0<ξi<1,所以0<ti{wTϕ(xi)+b}<1，即，其对应的样本点在分类正确的间隔中。

4.当ξi=1,αi=C时，此时样本点在SVM决策面上，是支持向量，被正确分类，样本点满足：ti{wTϕ(xi)+b}=0。
变量关系：这里的变量关系的分析和第三种情况一样，差别仅仅是 ξi=1，由：ti{wTϕ(xi)+b}=1−ξi，可以很容易知道：ti{wTϕ(xi)+b}=0 ，这样，样本点xi就刚好在SVM的决策面上了。

5.当ξi>1,αi=C时，是支持向量，被错误分类，样本点满足：ti{wTϕ(xi)+b}<0。
变量关系：这里的变量关系的分析和第三种情况一样，差别仅仅是 ξi>1，由：ti{wTϕ(xi)+b}=1−ξi，可以很容易知道：ti{wTϕ(xi)+b}<0 ，这样，样本点xi就在决策面错误的一边，被错误分类了。

由于变量α是我们最终要求解的变量，这里再单独对变量α做一个总结。首先，这里取g(x)如下，即SVM的决策面函数:

g(x)=∑i=1N{αiti<ϕ(xi),ϕ(x)>}+b

那么，根据前面的表格，可以很容易得到：

αi=00<αi<Cαi=C⇔tig(xi)≥1⇔tig(xi)=1⇔tig(xi)≤1

总的来说就是：

• 在SVM间隔区间外的点，对应的αi=0
• 在SVM间隔区间边缘上的点，对应的0<αi<C
• 在SVM间隔区间内部的点，对应的αi=C

支持向量机（SVM）三

标签： svm

2016-07-31 16:55 834人阅读 评论(0)收藏举报

分类：

监督学习（11）

版权声明：本文为博主原创文章，未经博主允许不得转载。

目录(?)[+]

支持向量机（SVM）

标签（空格分隔）： 监督学习

---

@author : [e-mail]
@time : 2016-07-31

---

---

---

三、基于核函数的非线性SVM

使用上面提到的 软间隔最大化分类器 在一定程度上，可以解决非线性可分问题。但是，其实质上是用一个线性的决策面，在允许部分训练样本点出现分类错误的前提下，得到的SVM。软间隔最大化分类器 对于数据是近似线性可分的情况，效果还是不错的，但是对于完全的线性不可分的情况，其分类效果就不太好了。此时，就需要通过某种手段，将SVM从线性分类器扩展成为非线性分类器，而这个手段，就是“核技巧”。

核技巧在机器学习中的应用是非常的广泛的，特别是从2000年之后，各个大牛们对核技巧的研究也越来越深入，这里仅仅对核技巧做一些简单的说明，方便在SVM中使用，后面会使用专门的文章来详细讨论核技巧。

在前面对SVM的推导中，最后得到的判别函数为：

f(x)=sign{∑i=1N{α∗iti<ϕ(xi),ϕ(x)>}+b∗}

上式中有两个东西需要格外注意，ϕ(xi)和<\phi(x_i),\phi(x)>

ϕ(xi)所代表的就是一种空间映射，是核技巧必备的一个元素，这也是为什么本文从一开始推导SVM的公式的时候，使用的就是ϕ(x)而不是单纯的x的原因。

<ϕ(xi),ϕ(x)> 指的是 ϕ(xi),ϕ(x) 的內积。这里可以看到，SVM的判别函数最终变成了ϕ(xi),ϕ(x)的內积的求解。

实际上，这两点，就是核技巧的核心，下面分别对这两点进行说明：

---

3.1 特征映射解决非线性可分问题

一般来说，如果能用一个超曲面将正负训练样本完全分开，则称这种问题为非线性可分问题。

非线性可分问题一般是非常的难求的，对于近似线性可分的非线性可分问题，还可以考虑使用上面的 软间隔最大化的SVM来得到一个分类器，但是如果数据非线性十分的强，以至于无法近似线性分开的时候，我们一般就考虑对数据空间做一个空间变换，将维度提升，在低维空间中非线性可分的问题，在高维空间中可能变成线性可分的问题，在高维空间中训练一个线性分类器，对数据进行分类。

注意：维度提升后，在高维空间，是可能变成线性可分！！！是可能！！！，说白了，数据从低维空间映射到高维空间之后，到底会成什么状态，没人说得准。虽然从低维到高维之后，数据是否线性可分，存在不确定性，但也不失为一种有效的手段，并且，其在实际的应用中表现的也还不错。这个就像深度学习算法一样，那货到底干了什么事情，没人说得准，反正最终效果还不错。

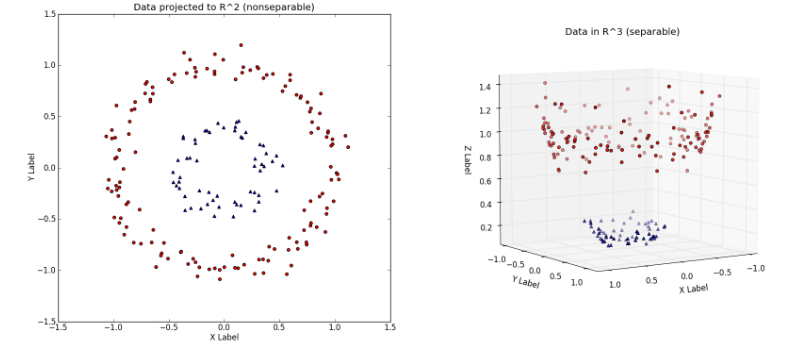
提升维度的过程大致可以从下面这个例子中看出来：

左图中对应的就是原始数据，显然左图中的数据是线性不可分的。然后通过映射：

[x1,x2]=>[x1,x2,x21+x22]

将数据从原始特征空间映射到新的特征空间。即，原始特征空间X是二维的,X中的样本点可以用[x1,x2]来表示，新的特征空间Z是三维的，Z中的样本点可以用[z1,z2,z3]来表示。这样，上面的映射过程，就可以表示为：

z1=x1z2=x2z3=x21+x22

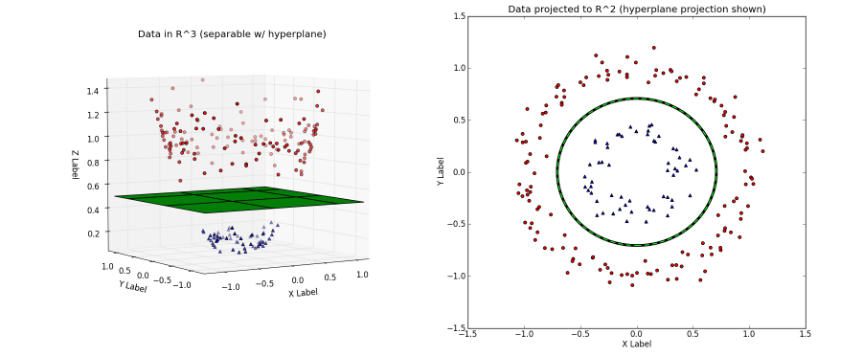
左图对应的是新的空间中，用一个平面就将变换后的数据分开；右图则对应原始空间中需要一个分线性的决策面，才可以将数据分开。

可以很容易的看出，在新的特征空间Z中，数据已经是线性可分的了。这就是提升数据维度，使得原空间的分线性可分问题变成新空间的线性可分问题的过程。

上面的例子说明，用线性模型求解非线性分类问题分为两个步骤：1、首先使用一个变换，将原空间的数据X映射到更高维度的新空间Z；2、在新的数据空间Z中,用线性分类学习方法，从训练数据中学习模型。

---

3.2 核函数K(x1,x2)

前面也提到过，在前面对SVM的推导中，最后得到的判别函数为：

f(x)=sign{∑i=1N{α∗iti<ϕ(xi),ϕ(x)>}+b∗}

从公式中可以明显看出，对这个判别函数的求解最终变成了对<ϕ(xi),ϕ(x)>的计算。这里的ϕ(x)就是上面提到的特征变换，用于解决非线性可分的问题。

按照一般的思维方式，要求解<ϕ(xi),ϕ(x)>，那么，就需要我们先定义ϕ(x)，再根据xi,x，分别计算出ϕ(xi),ϕ(x)，最后计算出它们的內积。

这是一个非常繁琐的步骤，而且，由于对高维空间具体的数据分布知之甚少，我们并不能确定一个映射ϕ(x)是否一定能够使得原始数据在高维空间中线性可分，所以一般也很难确具体的映射公式定ϕ(x)；或者说，我们一般很难显式的定义出ϕ(x)。

既然如此，是否可以将<ϕ(xi),ϕ(x)>直接看成一个函数，不显式的定义ϕ(x)，而是给定了xi,x后，就直接将<ϕ(xi),ϕ(x)>计算出来的方法呢？有！这就是核函数！！！！

核函数的定义：假设，将原始的输入空间为X（可能是欧式空间Rn 或者是一个离散集合），新的特征空间为Z(希尔伯特空间)，如果存在一个从X到Z的映射：

ϕ(x):X→Z

使得对所有的x1,x2∈X,函数K(x1,x2)满足条件：

K(x1,x2)=<ϕ(x1),ϕ(x2)>

则称K(x1,x2)为一个核函数。其中ϕ(x)为映射函数，<ϕ(x1),ϕ(x2)>为ϕ(x1),ϕ(x2)的內积。

基于前面的讨论，可以得出结论:核技巧的想法就是，在学习与预测中，仅仅定义核函数K(x1,x2)，而不显式的定义映射函数ϕ(x)。

一般来说，直接计算K(x1,x2)相对比较容易，而通过<\phi(x_1),\phi(x_2)>的计算反而比较的复杂。

映射函数ϕ(x)一般是将原始空间的维度升高，有时候会变成无穷维度。

---

3.3 非线性映射定ϕ(x)与核函数K(x1,x2)的关系

• 对于给定的函数K(x1,x2)，其映射后的空间Z，可以使多样的，即可以映射到不同的特征空间中
• 对于给定的函数K(x1,x2)，即便映射到相同维度的特征空间，其映射函数ϕ(x)也存在多样性

为了说明上面这两个特点，这里举个例子：假设，输入空间是X=R2,核函数是K(x1,x2)=(x1∗x2)2
1. 取特征空间Z=R3，即维度升高一个维度，此时ϕ(x)可以取：

ϕ(x)=[(x(1))2,2√x(1)x(2),(x(2))2]T

或者也可以取：

ϕ(x)=12√[(x(1))2−(x(2))2,2x(1)x(1),(x(1))2+(x(2))2]T

1. 取特征空间Z=R4，即维度升高两个维度，此时ϕ(x)可以取：

ϕ(x)=[(x(1))2,x(1)x(2),x(1)x(2),(x(2))2]T

---

3.4 常用的核函数

此处本应该讲讲，如何来构造核函数的，但是这个知识点实在是太过复杂，直接放在后面专门讲核技巧的文章中。

一个函数是否能称为核函数，是有非常严格的要求的，但是，我们在实际的使用中，一般都会使用一些常用的核函数，这里提供四个最常用的核函数，关于这些常用核函数的说明，也将放在后面专门讲核函数的文章中。

1.Polynomial 核函数：

K(x,z)=(x,z)d;d∈N

2.Gaussian 核函数：

K(x,z)=exp(−||x−z||22σ2);σ>0

3.Sigmoid 核函数：

K(x,z)=tanh(α<x,z>+β);α>0,β>0

4.RBF 核函数：

k(x,z)=exp(−ρd(x,z));ρ>0,d(x,z)是任意的距离度量

---

3.5 对无穷维度的定性理解

每次在读一些关于核函数的书籍或者网上的博客的时候，总是会提到：核函数不需要显示的定义特征空间Z以及特征映射ϕ(x)，使得学习算法隐式的在高维的特征空间中进行，甚至可以在无穷维度中进行。

这句话的前部分，已经说明过了，核函数的确不需要显示的定义特征空间Z以及特征映射ϕ(x)，就是可以完成学习过程。但是，甚至可以在无穷维度中进行到底是怎么回事？我所看到的书籍和网络博客中，却没有进一步的讨论。我在这里做一个简略的说明，这需要会涉及一些核函数构造的知识，比较复杂，这里仅仅做定性的分析，详细的讨论也会放在后面专门讲解核技巧的文章中。

在高等数学中，有无穷级数的概念，举个简单的例子：

exp(x)=∑n=0∞xnn!;−∞<x<∞

根据上面这个无穷级数的式子，可以很容易的推断出，指数型的核函数，可以变成无穷维度的多项式映射的结果：

k(x,z)=exp(k1(x,z))=∑m=0∞(k1(x,z))mm!

对于Gaussian 核函数:

K(x,z)=exp(−||x−z||22σ2);σ>0

由于这是一个指数型的核函数，根据前面的讨论，可以定性的判断出，基于无穷级数，Gaussian 核函数的映射函数，可以是无穷维度的。其具体的公式会在后面专门讲核函数的文章中说明，这里仅仅是一个定性的理解。

下面，以一分代码来说明一下SVM的应用：

# -*- coding: utf-8 -*-

"""
@author: [e-mail]
@time: 2015-07-17_13-59

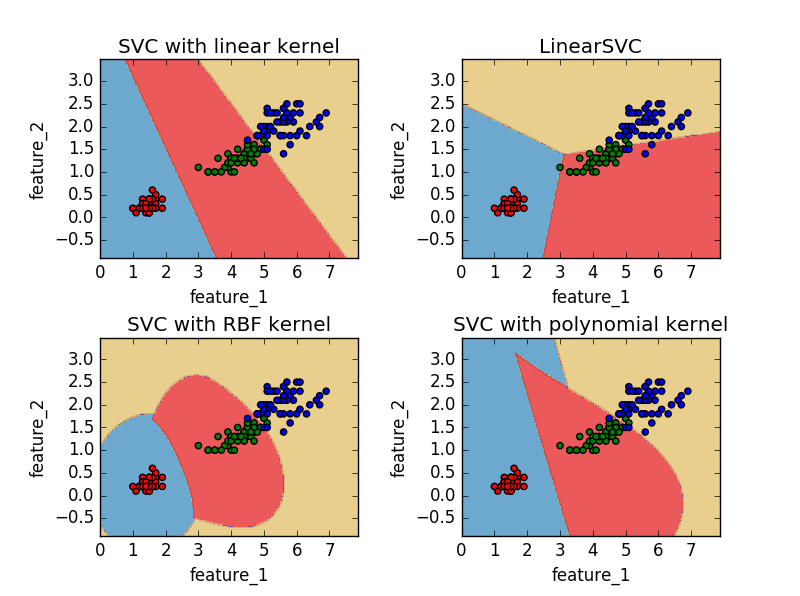
SVM分类算法示例

为了绘图方便，这里仅仅使用iris数据集的前两个特征作为样本特征

LinearSVC 使用的是平方合页损失
SVC（kernel=‘linear’） 使用的是正则化合页损失

LinearSVC 使用留一法（one-vs-rest）处理多类问题
SVC 使用的是one-vs-one的方法处理多类问题

从图中很容易看出one-vs-rest方法和one-vs-one所产生的决策面的区别

"""

print __doc__

import numpy as np
import matplotlib.pyplot as plt

from sklearn import svm, datasets

# 导入iris数据
# 这个数中一共有三个类别
# 每个类别50个样本
# 每个样本有四个特征
iris = datasets.load_iris()
X = iris.data[:, [2, 3]] # 这里仅仅两个特征作为样本特征
y = iris.target

C = 1.0 # SVM正则化参数

# 使用线性核学习SVM分类器
svc = svm.SVC(kernel='linear', C=C).fit(X, y)
# 直接使用线性SVM分类器
linear_SVC = svm.LinearSVC(C=C).fit(X, y)
# 使用rbf（径向基）核学习SVM分类器
rbf_svc = svm.SVC(kernel='rbf', gamma=0.7, C=C).fit(X, y)
# 使用多项式核学习SVM分类器
poly_svc = svm.SVC(kernel='poly', degree=3, C=C).fit(X, y)

# 生成绘图用的网格
x0_min, x0_max = X[:, 0].min() - 1, X[:, 0].max() + 1
x1_min, x1_max = X[:, 1].min() - 1, X[:, 1].max() + 1

xx0, xx1 = np.meshgrid(np.arange(x0_min, x0_max, 0.02),
                       np.arange(x1_min, x1_max, 0.02))

titles = ['SVC with linear kernel',
          'LinearSVC',
          'SVC with RBF kernel',
          'SVC with polynomial kernel']

color = ['r']*50 + ['g']*50 + ['b']*50

for i, clf in enumerate((svc, linear_SVC, rbf_svc, poly_svc)):
    plt.subplot(2, 2, i + 1)
    plt.subplots_adjust(wspace=0.4, hspace=0.4)

    z = clf.predict(np.c_[xx0.ravel(), xx1.ravel()])
    z = z.reshape(xx0.shape)

    plt.contourf(xx0, xx1, z, cmap=plt.cm.Paired, alpha=0.8)
    plt.scatter(X[:, 0], X[:, 1], c=color)

    plt.xlabel('feature_1')
    plt.ylabel('feature_2')
    plt.xlim(xx0.min(), xx0.max())
    plt.ylim(xx1.min(), xx1.max())
    plt.title(titles[i])

plt.show()

---

---

其实，关于SVM算法，如果是入门，看到这个地方，就已经不用再往下深究了。后面是SMO算法的推导，如果不清楚，并不影响SVM的理解。

---

---