线性判别函数

---

线性判别函数用来对线性可分的数据进行分类
判决方程：g(x)=WTx+w0
其中，x为d维列向量
判别规则：
对于二类分类，判决规则为：
当g(x)>0判决为类别1：ω1
当g(x)<0判决为类别2：ω2
等于0的情况为不可分。

---

齐次化

为了便于分析，通常将数据进行齐次化，也就是使得判决方程g(x)过原点。
具体操作：

g(x)=aTya=(w0,WT)Ty=(1,x)T

也就是说原来我们需要求解W和w0，现在只需要求解a即可

规范化

由上面判决规则可知：

aTy>0,当x属于类别ω1aTy<0,当x属于类别ω2

如果对于线性可分的数据，如果我们将ω2的数据y变成−y，则对于所有的样本都有aTy>0。

---

感知准则函数

将样本齐次化和规范化后我们可将损失函数定义为：

J=∑y∈Yk−aTyYk是所有错分样本的集合，即：Yk={y|aTy<=0}

这完全符合我们的认知，当错误样本越多J=∑y∈Yk−aTy越大，所以要使得J最小，即达到了我们的目的。

要使得J最小，可采用梯度下降法，对a求偏导得：
∂J∂a=−∑y∈Yky
故更新a=a−∂J∂a=a+ηk∑y∈Yky
ηk为步长，应当大于0，一般使得ηk越来越小，其实这也符合我们的认知，在还没接近最小点时应该以较快的速度下降（即η较大），而在接近最小点时应当小心翼翼地接近最小点（即η较小）。但是实际当中η的取值在线性可分的情况时，可以越来越大，并不会影响收敛，但是当在线性不可分时则应该使之越来越小从而使得“坏样本”（线性不可分的点）对a的影响尽可能的小。
具体算法往往有如下几种：
1.可变增量批处理感知准则函数：
可变指ηk可变，批处理指在更新a时考虑了多个样本：∑y∈Yky

其实对上述算法有个最直接的改进便是在判断错分样本时的标准严格一点，
即：原来是认为aTy<0为错分样本，现在认为aTy<b（b为一个正常数）便认为被错分。
这么做的理由可见如下分析：
当我们在求解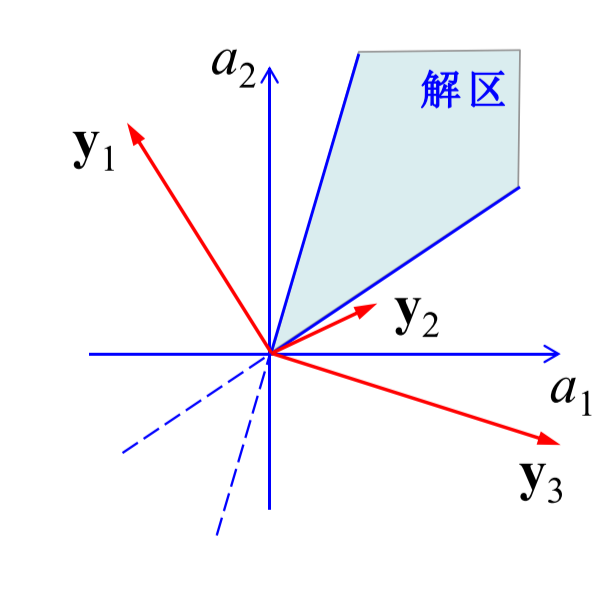a时，实际是寻找一个解向量a能够使得对于所有的样本满足aTy>0，即被限制在所有样本的法向量之间，几何图示为：

a为解区内的任何一个向量，显然这样a的取值会比较宽泛，如果能够取在靠近解区中心的区域则会更加理想，所以有了采用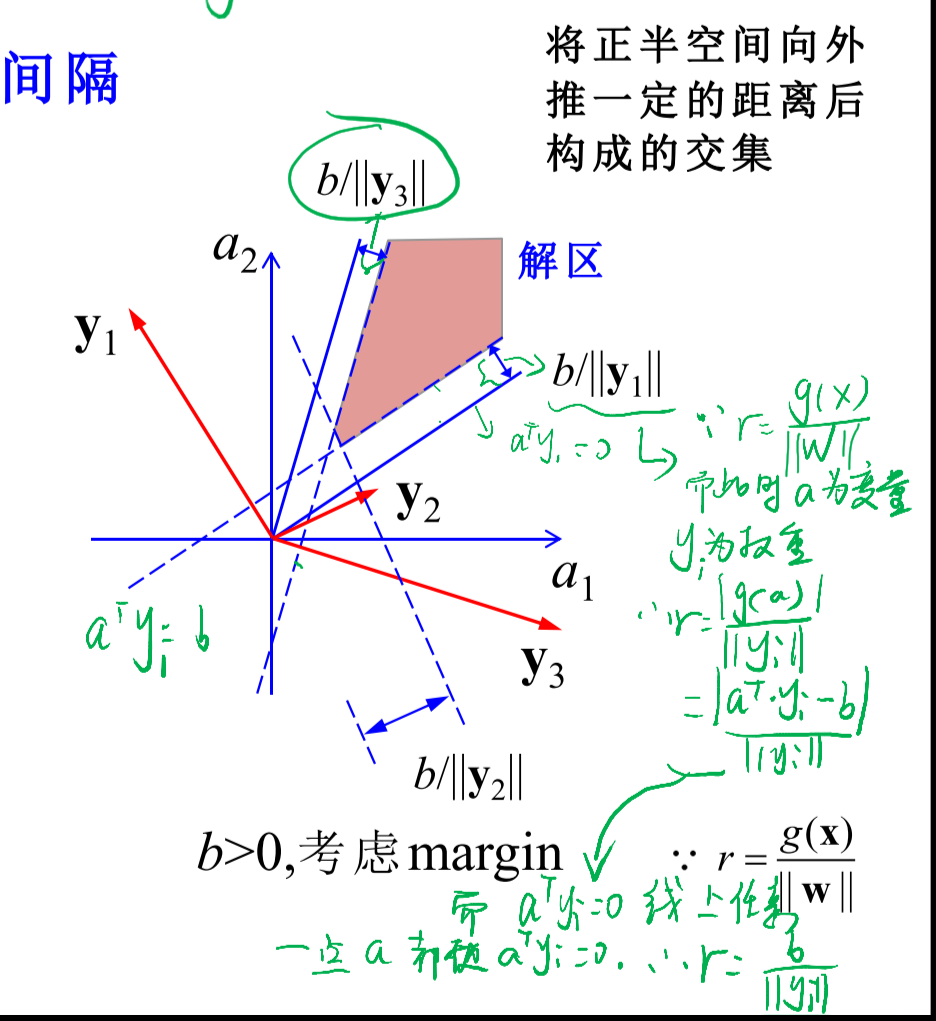aTy>b的措施，几何图示为：

具体算法只需将y错分的准则改为aTy<b即可。
(其实我想不出这线性判别函数和SVM有什么区别，感觉都是一样的思想啊，而为了取得更好的效果都增加了一个裕量b,没准等系统学习了SVM就了解了)
2.固定增量批处理感知准则函数
没什么新的，就是将ηk设为固定即可
3.固定单样本感知准则函数
之前都是先统计出所有错误的样本，而现在是发现一个错误样本便修改一次。
更新a的准则为ak+1=ak+ηkyk,yk为第k个样本
具体算法为：

要注意的是k是在一直累加的，是会超过样本个数n的，如果yk处的k不加修改直接使用是会报错的，所以对于yk的k要进行mod n处理，即：k=kmodn(k除以n,而后取余数）

---

MSE算法

之前的感知准则函数都是采用的错误样本来构建的损失函数，而MSE的是采用所有的样本进行构建损失函数。
MSE的思想为：
认为对于所有的样本yi,都会有aTyi=bi>0。
设Y为样本矩阵，行为样本，列为样本的特征，则可以写成：

图中所画绿色圈为一个样本
则对于所有样本会有如下方程：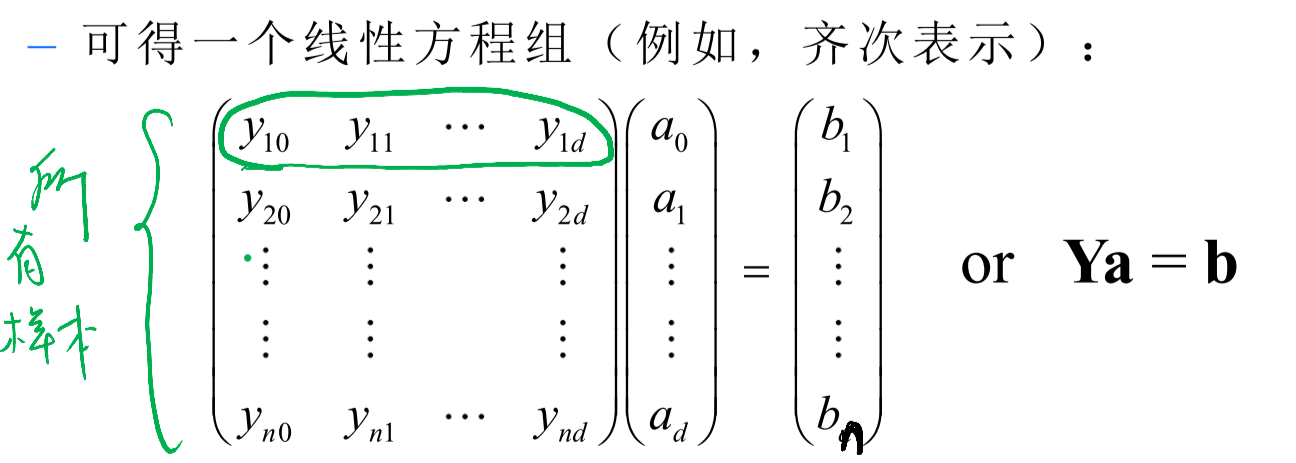

则我们可以直接解出a=Y−1b
但是往往n>>d易导致Y奇异，并且实际操作中不可能找到一个a使得Ya=b，肯定是会有所偏差，故而定义一个误差项e=Ya−b
,我们优化的目标便是使得误差最小即可。
故可定义损失函数：
J=12|e|2=|Ya−b|2=12(Ya−b)T(Ya−b)
同样求偏导数：
∂J∂a=YT(Ya−b)
损失函数是一个凸函数（其二阶导大于0），故使的偏导数等于0便可求解a.
a=(YTY)−1YTb，其中(YTY)−1YT是Y的伪逆。
但是当y维数很高时，计算违逆的复杂度高，故而可考虑梯度下降法：
ak+1=ak+ηkYT(b−Yak)
具体算法为：

这里要注意的是，ηk需要让其随着k增大而减小，来保持算法收敛。

---

Ho-Kashyap算法

在MSE算法时，我们认为b是已知的，是自己设置的一个正数，而Ho-Kashyap算法认为b是未知的，需要自己求出来。
于是损失函数：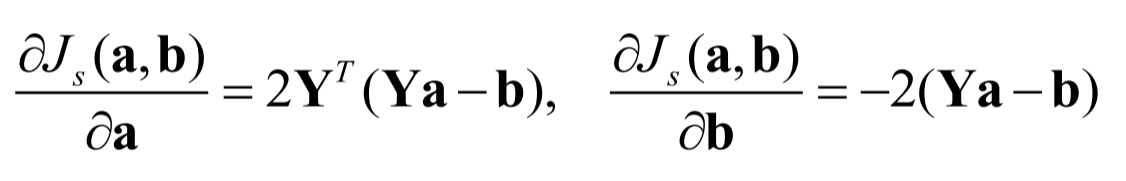
J=|Ya−b|2现在具有a,b两个参数，需要对其分别求偏导：

a=Y+b,Y+为Y的伪逆
b采用梯度下降进行求解
bk+1=bk−ηk∂J∂b
但是因为b需要一直大于0，于是可以进行如下构造：

故而始终保证了b大于0.
具体算法为：

---

简单的实例：

有数据如下：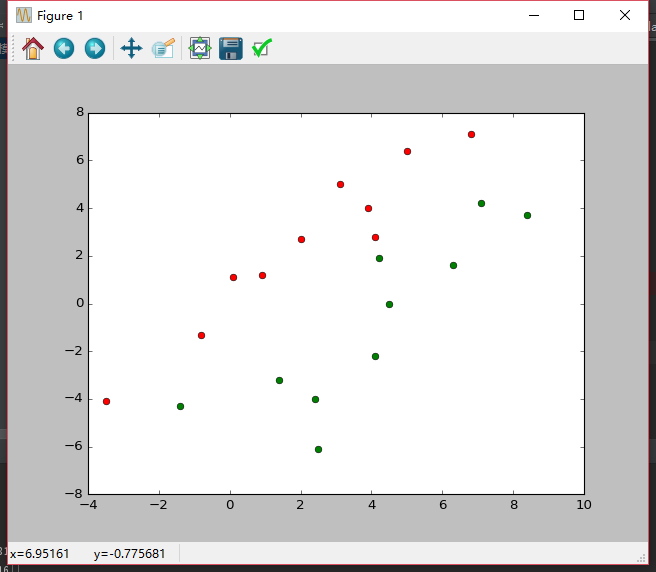

采用可变增量批处理感知器进行分类：
η=0.5,ηk+1=etak−0.0004(设置了最大迭代次数为1000保证其不会大于0)，a初始为0向量，迭代次数为24次
得：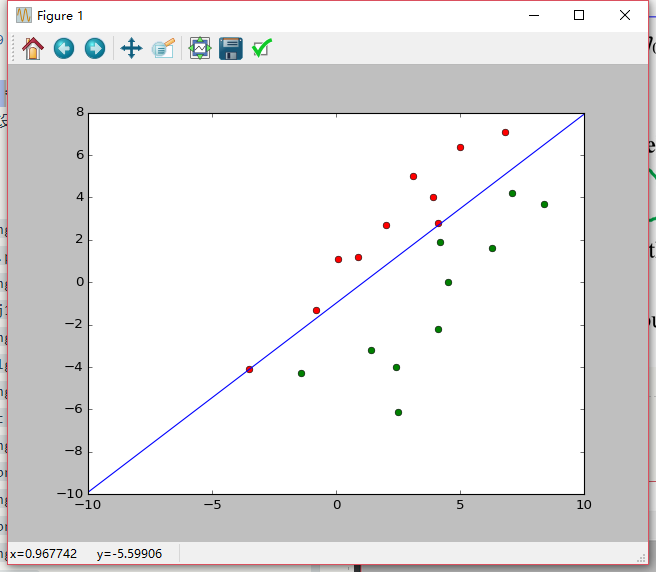

还是采用可变增量批处理感知器进行分类：，只是在判断错误样本时认为aTy<30为错误样本。
迭代次数为：343次
结果会比单纯的可变增量批处理感知器好：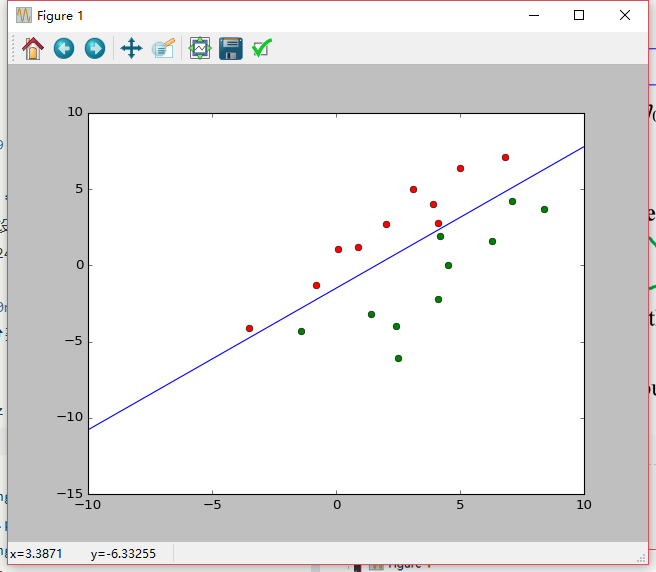

采用H-K算法：
η0=1,ηk+1=0.9998∗etak,a初始为全0向量，b初始为全1向量，bmin=0.1∗b
迭代次数为：352次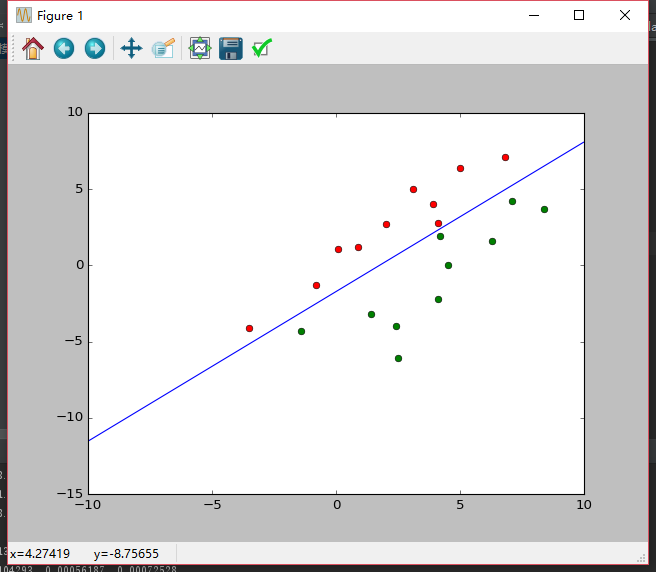

损失函数收敛图为：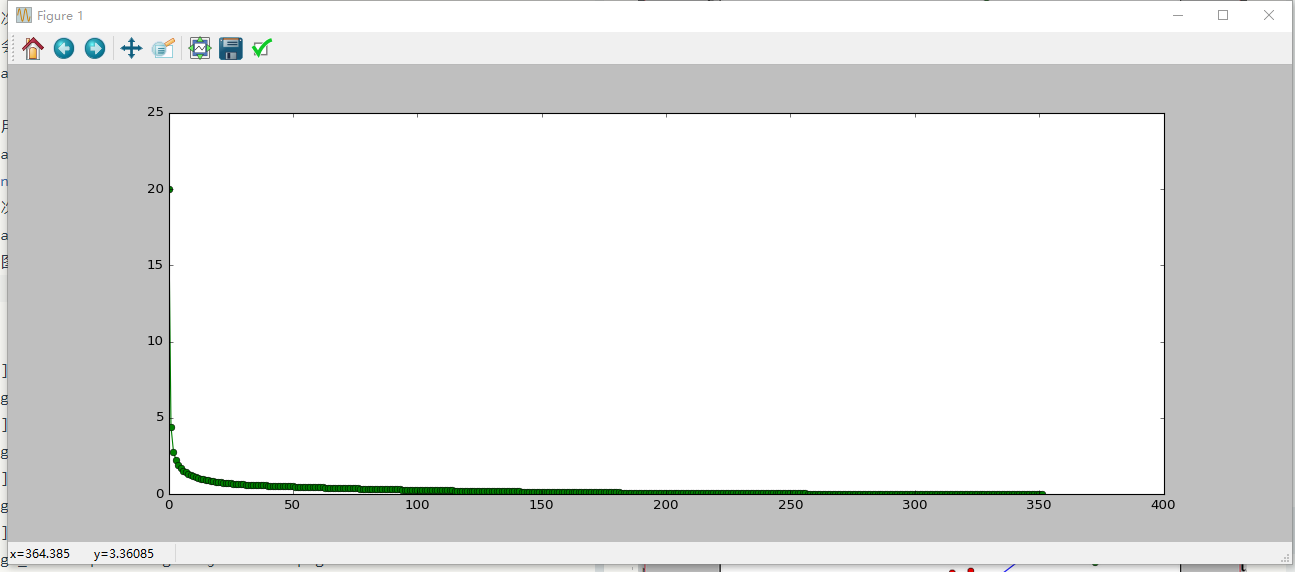

坐标轴取短一点则得如下图：