台大机器学习——可行性证明2

来源：互联网发布：高级计量经济学知乎编辑：程序博客网时间：2024/05/21 08:05

回顾与预览
基于统计的学习流程：
--- 如果备选函数集的大小|H|=M，M有限，训练数据量N足够大，则对于学习算法A选择的任意备选函数h，都有
E-out(h)≈E-in(h)
--- 如果A找到了一个备选函数，使得E-in(h)≈0，则有很大概率E-out(h)≈0 ---》学习是可能的
可以讲，机器学习有两个核心问题：
1. 我们能否保证E-out(h)与E-in(h)足够接近？
2. 我们能否使E-in(h)足够小？
对于M→∞的情况，能否把它reduce到有限，是这一讲将要讨论的问题。
二元分类的 Effective Number
回顾一下霍夫丁不等式的推导：
在训练数据集D上，有一个不好的备选函数h使得

只要有一个h不好，就可以认为这个H与D的搭配是不好的

为了让A能够自由选择，我们要求这个坏事件的发生概率必须小于某一个可以接受的值，考虑最坏的情况，利用Union Bound 获得上述概率的上限

从而得到第4讲中的霍夫丁不等式。
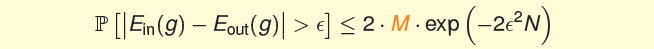
这里Union Bound所代表的情况只有在M个事件没有交集的时候才发生。
因此Union Bound过于高估了坏事件发生概率的上限。

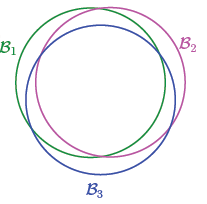
具体来说，假如有两个相似的备选函数h1≈h2，则有

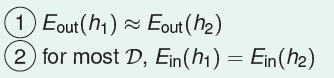
即h1与h2在D上几乎是同好或同坏的，或曰B1与B2高度相关，P[B1]与P[B2]可以合并，但Union Bound却将他们相加了。
解决过分估计的问题，可以将备选函数集分类，相似的函数分在一起。
以二元分类问题为例，备选函数集为

其中有无数条线。
当只有一个输入时，这些线可以被分成两类。

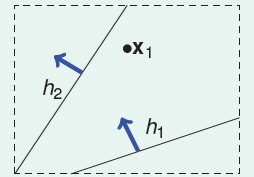
第一类，输出为○；第二类，输出为×。
输入变成2个：

显然有4种划分。
输入变成3个：
可以有8种划分；
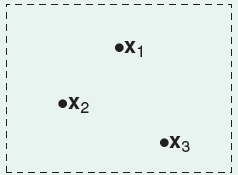
也可能只有6种。

此时3个输入共线。
所以3个输入情况下最多8种划分；
输入变成4个：

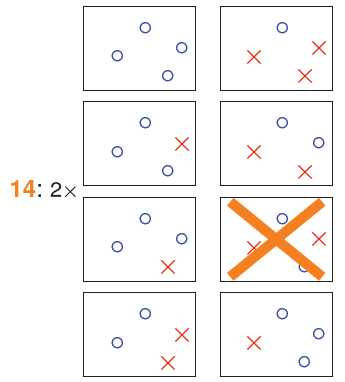
最多14种划分。
综上，N个输入下线性划分的最大个数即线性划分有效数（Effective Number of Lines），这里可以理解成有效划分。
由于是二分类问题，线性划分有效数一定 ≤ 2^N，我们希望：
1. 用线性划分有效数代替M，从而将无限reduce到有限；

2. 线性划分有效数 << 2^N，从而坏事件的发生概率上限不至于随着N的增大而指数增长。
一般备选函数的 EffectiveNumber
备选函数集中的每一个函数h都是输入X到输出Y的一个映射：

将

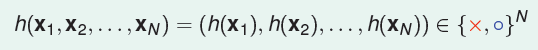
定义为h对D的一个Dichotomy(二分)。
所以
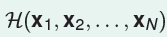
就包括了所有对D的dichotomies。
定义成长函数（Growth Function）为：
即成长函数是在N个输入上dichotomies的最大数量。
举个例子，平面二元分类，输入为3时，如果3个点共线，有6个划分，如果3个点不共线也不重合，有8个划分，所以此时成长函数值为8。
----------------------------------------------------------------------------------------------
Positive Ray

输入（x1,x2,...,xN）分布在实数轴上，确定一个分割点a，大于a的输出+1，小于a的输出-1。

显然，有N个输入，实数轴被分成N+1段，Positive Ray的成长函数为

此时N+1 << 2^N （N is large）。
----------------------------------------------------------------------------------------------
Positive Interval

输入（x1,x2,...,xN）分布在实数轴上，确定一个范围[ l, r )，在范围内的输出+1，其他输出-1。
N个输入，实数轴被分成N+1段，从其中任选两段构成一个interval，或两端落在同一段中，Positive Interval的成长函数为

且
----------------------------------------------------------------------------------------------
Convex Set - 凸集

顾名思义，划分区域必须是凸的。左图蓝色区域是凸集，右图则不是。

凸集的成长函数长什么样？
假设N个输入（x1, x2, ..., xN）在2维空间中刚好位于一个圆上，给定任意一种dichotomy，总能找出一个凸集刚好包含了所有+1的点，并将-1的点排斥在外。
即
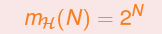
此时我们已经找到了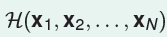的上限，从而不必关心N个输入不在一个圆上的情况。我们可以说：（这个概念很绕但是很重要！）
break point
在霍夫丁不等式中，用成长函数代替M：

如果成长函数是指数函数，则随着N的增大，概率上限也急剧增加，所以我们希望成长函数是多项式。
回顾下上一小节的4个成长函数：
Positive Ray和Positive Interval的成长函数是多项式，而Convex Set的成长函数是指数函数。那2D-PLA的成长函数是多项式吗？
为了回答这个问题，引入一个新概念 - Break Point。
有k个输入，如果它不能被当前的备选函数集H shatter，那么k就是H的一个Break Point。
或者说对于任意k个输入，H都无法穷尽所有可能的划分。
这里讨论的Break Point指的是minimum break point k，也就是第一个被shatter的N。
对于2D-PLA，break point k = 4。

说了半天，Break Point 与成长函数的成长性到底有什么关系？

首先我们能确定，对于二元分类问题，如果一个H没有break point，给定任意N，一定能找到N个输入，H能穷尽它的所有划分，此时：

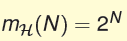
如果 break point = k 从上图可以猜测：
如果猜测成立，那么只要N足够大，训练结果的正确性就有保障了！让我们下一讲讨论。
补充：关于 “shatter”与 “break point”这两个有点晦涩的概念，我在课程论坛里看到一个精彩的诠释，分享给大家。

这位仁兄的ID叫 -- beader。