程序博客网 > js 获取class值

可视化与多维数据分析

来源：互联网发布：js 获取class值编辑：程序博客网时间：2024/05/13 22:02

可视化数据是把数据转换成视觉或表格的形式，以便可以分析数据和数据项或属性之间的关系与特性。

可视化基本步骤：

1.表示

2.安排

3.选择

可视化技术：1.直方图、多维直方图 2.盒状图（通常显示数据内部的变化）

3.散布图矩阵。下面转载一篇关于介绍散布矩阵的博文如下（地址http://blog.csdn.net/breeze5428/article/details/25612763）：

因为最近需要用到散布矩阵做数据分析，因此在此做些关于散布矩阵的小总结。在多变量概率统计中，散布矩阵是用来估计多维正态分布协方差的统计量。

定义

给定n个 $m$ 维的样本，用矩阵 $m\times n$ 的矩阵 $X$ 表示以上数据，其中 $X=[x_1,x_2,\cdot\cdot\cdot,x_n]$ 。于是可得样本的均值为

$\overline{\mathbf{x}} = \frac{1}{n}\sum_{j=1}^n \mathbf{x}_j$

其中 $\mathbf{x}_j$ 是矩阵 $X\,$ 的第 $j$ 列.

散布矩阵为 $m\times m$ 的半正定矩阵

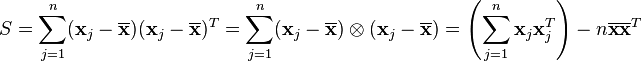
$S = \sum_{j=1}^n (\mathbf{x}_j-\overline{\mathbf{x}})(\mathbf{x}_j-\overline{\mathbf{x}})^T = \sum_{j=1}^n (\mathbf{x}_j-\overline{\mathbf{x}})\otimes(\mathbf{x}_j-\overline{\mathbf{x}}) = \left( \sum_{j=1}^n \mathbf{x}_j \mathbf{x}_j^T \right) - n \overline{\mathbf{x}} \overline{\mathbf{x}}^T$

其中 $T$ 表示矩阵的转置。散布矩阵可以简要的表示为

$S = X\,C_n\,X^T$

在此， $\,C_n$ 定义为centering matrix，具体定义为

$C_n = I_n - \tfrac{1}{n}\mathbb{O}$ 。

应用

在最大似然估计中，给定n个样本，一个多元正太分布的协方差可以表示为归一化的散度矩阵：

C_{ML}=\frac{1}{n}S.

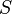若 $X\,$ 中的样本从多元正态分布中独立抽取，则 $S\,$ 服从Wishart分布.

与协方差的关系

以上仅是从维基百科上翻译过来的内容，不难发现散布矩阵和协方差矩阵的关系。散布矩阵前乘以系数1/n就可以得到协方差矩阵。如果熟悉PCA，我们就会发现可以利用散度矩阵做PCA。

4.等高线图：适用于连续属性是且空间网格测量时。

5.平行坐标：用来绘制高维数据的属性值，采用同一平行轴与垂直轴

OLAP操作：

切片，切块，向上浏览，向下浏览

0 0

js 获取class值

js 获取class值

原创粉丝点击

热门问题 老师的惩罚人脸识别我在镇武司摸鱼那些年重生之率土为王我在大康的咸鱼生活盘龙之生命进化天生仙种凡人之先天五行春回大明朝姑娘不必设防，我是瞎子评书白眉大侠全集白眉大侠武功排名暴走大侠修改器暴走大侠破解版下载白眉大侠全320回高清版白眉大侠全320回全集梦见大便大便成形大便带血痛大便成型大便颜色大便粘液梦见拉大便大便臭大便是黑色大便干婴儿大便婴儿大便小孩大便婴儿的大便大便便大便有宝宝大便干大便英文宝宝大便大便图大便的图片大便照片大便超人大便正常幼儿大便正常大便大便形状宝宝的大便大便英语大便很困难大便有黑色大便黑色大便深褐色大便青黑色大便完