Codeforces 763B Timofey and rectangles（四色定理）（思维）

Timofey and rectangles

One of Timofey’s birthday presents is a colourbook in a shape of an infinite plane. On the plane n rectangles with sides parallel to coordinate axes are situated. All sides of the rectangles have odd length. Rectangles cannot intersect, but they can touch each other.

Help Timofey to color his rectangles in 4 different colors in such a way that every two rectangles touching each other by side would have different color, or determine that it is impossible.

Two rectangles intersect if their intersection has positive area. Two rectangles touch by sides if there is a pair of sides such that their intersection has non-zero length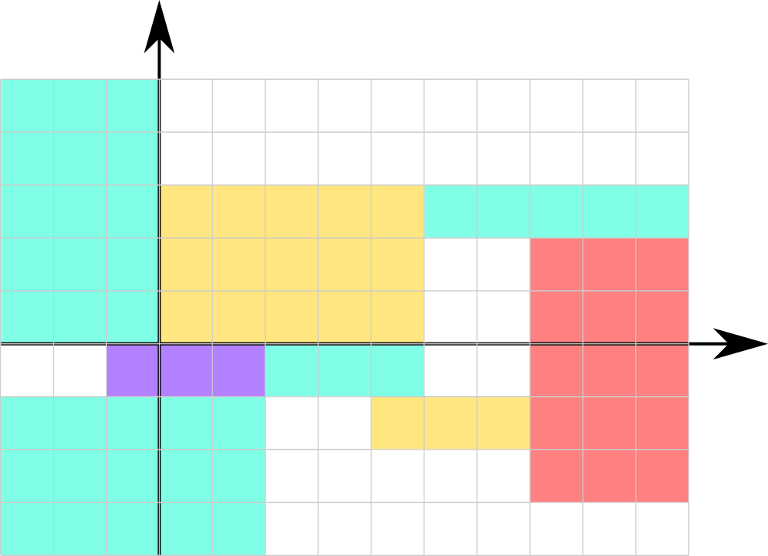

The picture corresponds to the first example

Input
The first line contains single integer n (1 ≤ n ≤ 5·105) — the number of rectangles.

n lines follow. The i-th of these lines contains four integers x1, y1, x2 and y2 ( - 109 ≤ x1 < x2 ≤ 109,  - 109 ≤ y1 < y2 ≤ 109), that means that points (x1, y1) and (x2, y2) are the coordinates of two opposite corners of the i-th rectangle.

It is guaranteed, that all sides of the rectangles have odd lengths and rectangles don’t intersect each other.

Output
Print “NO” in the only line if it is impossible to color the rectangles in 4 different colors in such a way that every two rectangles touching each other by side would have different color.

Otherwise, print “YES” in the first line. Then print n lines, in the i-th of them print single integer ci (1 ≤ ci ≤ 4) — the color of i-th rectangle.

Example
input
8
0 0 5 3
2 -1 5 0
-3 -4 2 -1
-1 -1 2 0
-3 0 0 5
5 2 10 3
7 -3 10 2
4 -2 7 -1
output
YES
1
2
2
3
2
2
4
1

题意：给出n个矩形的左下角和右上角的坐标定点，并保证矩形边长为奇数，给矩形涂色并保证相接触的矩形颜色不同，问能否用四种不同的颜色完成

分析：根据四色定理知道，四种颜色一定能完成染色。 （表示对四色定理毫不知情~Orz）

因为所有矩形的边长均为奇数，所以可以根据矩形左下角纵横坐标的奇偶性来把矩形分为四类（奇奇，偶偶，奇偶，偶奇）
偶偶涂1号色，偶奇涂2号色，奇偶涂3号色，奇奇涂4号色

代码：

#include<stdio.h>#include<stdlib.h>int main(){    int n,a,b,c,d;    scanf("%d",&n);    printf("YES\n");    while(n--)    {        scanf("%d%d%d%d",&a,&b,&c,&d);        printf("%d\n",2*(abs(a)&1)+(abs(b)&1)+1);    }    return 0;}

ps：我这种智商弱爆了的真是不适合做这种题啊~Orz