强化学习进阶第六讲策略梯度方法

来源：互联网发布：淘宝达人推广费多少钱编辑：程序博客网时间：2024/05/17 01:17

转载自知乎专栏天津包子馅儿的知乎

说明：从这讲开始，我们进入强化学习的进阶课程学习。进阶课程以强化学习入门第一讲到第五讲为基础，所以请读者先读前面的课程讲义。该进阶课程也有五讲，主要讲解直接策略搜索方法。内容涉及到近十几年比较主流的直接策略搜索方法。本课程参考资料是Pieter Abbeel 在NIPS2016给的tutorial，视频网址为：

Deep Reinforcement Learning Through Policy Optimization

图6.1 强化学习分类

如图6.1所示为强化学习的分类示意图，我们这一节讲解策略搜索方法。

我们首先要弄清楚，什么是策略搜索？

回忆第一讲到第五讲的内容，前面讲的是值函数的方法。广义值函数的方法包括两个步骤：策略评估+策略改善。当值函数最优时，策略是最优的。此时最优策略是贪婪策略。我们回忆下什么是贪婪策略。贪婪策略是指 $arg\\max_a\ Q_{\theta}\left(s,a\right)$ ，即在状态s，对应最大行为值函数的动作，是一个状态空间向动作空间的映射，该映射就是最有策略。利用这种方法得到的策略往往是状态空间向有限集动作空间的映射。

策略搜索是将策略进行参数化即 $\pi_{\theta}\left(s\right)$ ，利用线性或非线性（如神经网络）对策略进行表示，寻找最优的参数 $\theta$ 使得强化学习的目标：累积回报的期望 $E\left[\sum_{t=0}^H{R\left(s_t\right)|\pi_{\theta}}\right]$ 最大。

在值函数的方法中，我们迭代计算的是值函数，然后根据值函数对策略进行改进；而在策略搜索方法中，我们直接对策略进行迭代计算，也就是迭代更新参数值，直到累积回报的期望最大，此时的参数所对应的策略为最优策略。

在正式讲解策略搜索方法之前，我们先比较一下值函数方法和直接策略搜索方法的优缺点。其实正因为直接策略搜索方法比值函数方法拥有更多的优点，我们才有理由或才有动机去研究和学习及改进直接策略搜索方法：

（1）直接策略搜索方法是对策略 $\pi$ 进行参数化表示，与值函数方中对值函数进行参数化表示相比，策略参数化更简单，有更好的收敛性。

（2）利用值函数方法求解最优策略时，策略改进需要求解 $arg\\max_a\ Q_{\theta}\left(s,a\right)$ ，当要解决的问题动作空间很大或者动作为连续集时，该式无法有效求解。

（3）直接策略搜索方法经常采用的随机策略，能够学习随机策略。可以将探索直接集成到策略之中。

当然与值函数方法相比，策略搜索方法也普遍存在一些缺点，比如：

（1）策略搜索的方法容易收敛到局部最小值。

（2）评估单个策略时并不充分，方差较大。

对于这些缺点，最近十几年，学者们正在探索各种直接策略搜索的方法进行改进。

策略搜索方法已经成功应用的案例如图6.2所示

图6.2 直接策略搜索方法成功案例

从图6.2我们看出，直接策略搜索的方法主要应用在机器人领域。本节主要讲解策略梯度的方法，第七节会讲TRPO的方法，第八节会讲确定性策略搜索方法，第九节会讲GPS方法，第十节会讲逆向强化学习方法。这些方法之间的关系可用图6.3表示。

图6.3 策略搜索方法分类

策略搜索方法按照是否利用模型可以分为无模型的策略搜索方法和基于模型的策略搜索方法。其中无模型的策略搜索方法根据策略是采用随机策略还是确定性策略分为随机策略搜索方法和确定性策略搜索方法。随机策略搜索方法最先发展起来的是策略梯度方法；然而策略梯度方法存在着学习速率难以确定等问题，为了解决这个问题学者们提出了基于统计学习的方法，基于路径积分的方法，回避学习速率问题。而TRPO并没有回避这个问题，而是找到了替代损失函数，利用优化方法局部找到使得损失函数单调的步长，我会在下一讲重点讲解。

基于似然率来推导策略梯度

用 $\tau$ 表示一组状态-行为序列 $s_0,u_0,\cdots ,s_H,u_H$ , 符号 $R\left(\tau\right)=\sum_{t=0}^H{R\left(s_t,u_t\right)}$ ,表示轨迹 $\tau$ 的回报， $P\left(\tau ;\theta\right)$ 表示轨迹 $\tau$ 出现的概率；则强化学习的目标函数可表示为：

$U\left(\theta\right)=E\left(\sum_{t=0}^H{R\left(s_t,u_t\right);\pi_{\theta}}\right)=\sum_{\tau}{P\left(\tau ;\theta\right)R\left(\tau\right)}$

强化学习的目标是找到最优参数 $\theta$ 使得： $\max_{\theta}U\left(\theta\right)=\max_{\theta}\sum_{\tau}{P\left(\tau ;\theta\right)R\left(\tau\right)}$

这时，策略搜索方法，实际上变成了一个优化问题。解决优化问题有很多种方法，比如：最速下降法，牛顿法，内点法等等。

其中最简单，也是最常用的是最速下降法，此处称为策略梯度的方法。

即 $\theta_{new}=\theta_{old}+\alpha\nabla_{\theta}U\left(\theta\right)$ 。

问题的关键是如何计算策略梯度 $\nabla_{\theta}U\left(\theta\right)$ 。

我们对目标函数进行求导：

$\nabla_{\theta}U\left(\theta\right)=\nabla_{\theta}\sum_{\tau}{P\left(\tau ;\theta\right)R\left(\tau\right)}\]\[=\sum_{\tau}{\nabla_{\theta}P\left(\tau ;\theta\right)R\left(\tau\right)}\]\[=\sum_{\tau}{\frac{P\left(\tau ;\theta\right)}{P\left(\tau ;\theta\right)}\nabla_{\theta}P\left(\tau ;\theta\right)R\left(\tau\right)}\]\[=\sum_{\tau}{P\left(\tau ;\theta\right)\frac{\nabla_{\theta}P\left(\tau ;\theta\right)R\left(\tau\right)}{P\left(\tau ;\theta\right)}}\]\[=\sum_{\tau}{P\left(\tau ;\theta\right)\nabla_{\theta}\log P\left(\tau ;\theta\right)R\left(\tau\right)}$ (6.1)

最终策略梯度变成了求 $\nabla_{\theta}\log P\left(\tau ;\theta\right)R\left(\tau\right)$ 的期望，我们可以利用经验平均来进行估算。因此，当利用当前策略 $\pi_{\theta}$ 采样m条轨迹后，可以利用这m条轨迹的经验平均对策略梯度进行逼近：

$\nabla_{\theta}U\left(\theta\right)\approx\hat{g}=\frac{1}{m}\sum_{i=1}^m{\nabla_{\theta}\log P\left(\tau ;\theta\right)R\left(\tau\right)}$ (6.2)

从重要性采样的角度推导策略梯度：

目标函数为： $U\left(\theta\right)=E\left(\sum_{t=0}^H{R\left(s_t,u_t\right);\pi_{\theta}}\right)=\sum_{\tau}{P\left(\tau ;\theta\right)R\left(\tau\right)}$

利用参数 $\theta_{old}$ 产生的数据去评估参数 $\theta$ 的回报期望，由重要性采样得到： $U\left(\theta\right)=\sum_{\tau}{P\left(\tau |\theta_{old}\right)\frac{P\left(\tau ;\theta\right)}{P\left(\tau |\theta_{old}\right)}R\left(\tau\right)}\]\[=E_{\tau ~\theta_{old}}\left[\frac{P\left(\tau |\theta\right)}{P\left(\tau |\theta_{old}\right)}R\left(\tau\right)\right]$ (6.3)

导数为：

$\nabla_{\theta}U\left(\theta\right)=E_{\tau ~\theta_{old}}\left[\frac{\nabla_{\theta}P\left(\tau |\theta\right)}{P\left(\tau |\theta_{old}\right)}R\left(\tau\right)\right]$ (6.4)

令 $\theta =\theta_{old}$ ，我们可以得到当前策略的导数：

$\nabla_{\theta}U\left(\theta\right)|_{\theta =\theta_{old}}\]\[=E_{\tau ~\theta_{old}}\left[\frac{\nabla_{\theta}P\left(\tau |\theta\right)|_{\theta_{old}}}{P\left(\tau |\theta_{old}\right)}R\left(\tau\right)\right]\]\[=E_{\tau ~\theta_{old}}\left[\nabla_{\theta}\log P\left(\tau |\theta\right)|_{\theta_{old}}R\left(\tau\right)\right]$ (6.5)

从重要性采样的视角推导策略梯度，不仅得到了与似然率相同的结果，更重要的是得到了原来目标函数新的损失函数： $U\left(\theta\right)=E_{\tau ~\theta_{old}}\left[\frac{P\left(\tau |\theta\right)}{P\left(\tau |\theta_{old}\right)}R\left(\tau\right)\right]$

似然率策略梯度的直观理解

前面我们已经利用似然率的方法推导得到了策略梯度公式为： $\nabla_{\theta}U\left(\theta\right)\approx\hat{g}=\frac{1}{m}\sum_{i=1}^m{\nabla_{\theta}\log P\left(\tau ;\theta\right)R\left(\tau\right)}$

对这个公式中的两项，我们分别进行理解。

图6.4 策略梯度的直观理解示意图

其中第一项 $\nabla_{\theta}\log P\left(\tau ;\theta\right)$ 是轨迹 $\tau$ 的概率随参数 $\theta$ 变化最陡的方向，参数在该方向进行更新时，若沿着正方向，则该轨迹 $\tau$ 的概率会变大，而沿着负方向进行更新时，该轨迹 $\tau$ 的概率会变大。再看第二项 $R\left(\tau\right)$ ，该项控制了参数更新的方向和步长。 $R\left(\tau\right)$ 为正且越大则参数更新后该轨迹的概率越大； $R\left(\tau\right)$ 为负，则降低该轨迹的概率，抑制该轨迹的发生。

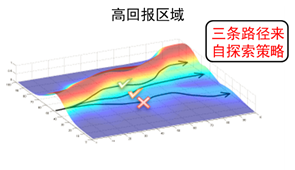
因此，策略梯度从直观上进行理解时，我们发现策略梯度会增加高回报路径的概率，减小低回报路径的概率。

前面我们已经推导出策略梯度的求解公式为： $\nabla_{\theta}U\left(\theta\right)\approx\hat{g}=\frac{1}{m}\sum_{i=1}^m{\nabla_{\theta}\log P\left(\tau ;\theta\right)R\left(\tau\right)}$

现在，我们解决如何求似然率的梯度： $\nabla_{\theta}\log P\left(\tau ;\theta\right)\textrm{？}$

已知 $\tau =s_0,u_0,\cdots ,s_H,u_H$ ，则轨迹的似然率可写为：

$P\left(\tau^{\left(i\right)};\theta\right)=\prod_{t=0}^H{P\left(s_{t+1}^{\left(i\right)}|s_{t}^{\left(i\right)},u_{t}^{\left(i\right)}\right)}\cdot\pi_{\theta}\left(u_{t}^{\left(i\right)}|s_{t}^{\left(i\right)}\right)$ (6.6)

式中， $P\left(s_{t+1}^{\left(i\right)}|s_{t}^{\left(i\right)},u_{t}^{\left(i\right)}\right)$ 表示动力学，式中无参数 $\theta$ ，因此可在求导过程中消掉。具体推导，如式（6.7）

$\nabla_{\theta}\log P\left(\tau^{\left(i\right)};\theta\right)=\nabla_{\theta}\log\left[\prod_{t=0}^H{P\left(s_{t+1}^{\left(i\right)}|s_{t}^{\left(i\right)},u_{t}^{\left(i\right)}\right)}\cdot\pi_{\theta}\left(u_{t}^{\left(i\right)}|s_{t}^{\left(i\right)}\right)\right]\]\[=\nabla_{\theta}\left[\sum_{t=0}^H{\log P\left(s_{t+1}^{\left(i\right)}|s_{t}^{\left(i\right)},u_{t}^{\left(i\right)}\right)}+\sum_{t=0}^H{\log\pi_{\theta}\left(u_{t}^{\left(i\right)}|s_{t}^{\left(i\right)}\right)}\right]\]\[=\nabla_{\theta}\left[\sum_{t=0}^H{\log\pi_{\theta}\left(u_{t}^{\left(i\right)}|s_{t}^{\left(i\right)}\right)}\right]\]\[=\sum_{t=0}^H{\nabla_{\theta}\log\pi_{\theta}\left(u_{t}^{\left(i\right)}|s_{t}^{\left(i\right)}\right)}$ (6.7)

从（6.7）的结果来看，似然率梯度转化为动作策略的梯度，与动力学无关。那么，如何求解策略的梯度呢？

下面，我们看一下常见的策略表示方法：

一般，随机策略可以写为确定性策略加随机部分，即：

$\pi_{\theta}=\mu_{\theta}+\varepsilon$

对于高斯策略： $\varepsilon \sim N\left(0,\sigma^2\right)$ ，是均值为零，标准差为 $\sigma$ 的高斯分布。像值函数逼近一样，确定性部分常见的表示为：

线性策略： $\mu\left(s\right)=\phi\left(s\right)^T\theta$

径向基策略： $\mu_{\theta}\left(s\right)=\omega^T\phi\left(s\right),\$ 其中：

$\phi_i\left(s\right)=\exp\left(-\frac{1}{2}\left(s-\mu_i\right)^TD_i\left(s-\mu_i\right)\right)$

参数为 $\theta =\left\{\omega ,\mu_i,d_i\right\}$

我们以确定性部分策略为线性策略为例来说明 $\log\pi_{\theta}\left(u_{t}^{\left(i\right)}|s_{t}^{\left(i\right)}\right)$ 如何计算。

首先 $\pi\left(u|s\right)~\frac{1}{\sqrt{2\pi}\sigma}\exp\left(-\frac{\left(u-\phi\left(s\right)^T\theta\right)^2}{2\sigma^2}\right)$ ，利用该分布进行采样，得到 $u_{t}^{\left(i\right)}$ ，然后将 $\left(s_{t}^{\left(i\right)},u_{t}^{\left(i\right)}\right)$ 带入，得到： $\nabla_{\theta}\log\pi_{\theta}\left(u_{t}^{\left(i\right)}|s_{t}^{\left(i\right)}\right)=\frac{\left(u_{t}^{\left(i\right)}-\phi\left(s_{t}^{\left(i\right)}\right)^T\theta\right)\phi\left(s_{t}^{\left(i\right)}\right)}{\sigma^2}$

其中方差参数 $\sigma^2$ 用来控制策略的探索性。

由此，我们已经推导除了策略梯度的计算公式： $\nabla_{\theta}U\left(\theta\right)\approx\hat{g}=\frac{1}{m}\sum_{i=1}^m{\left(\sum_{t=0}^H{\nabla_{\theta}\log\pi_{\theta}\left(u_{t}^{\left(i\right)}|s_{t}^{\left(i\right)}\right)}R\left(\tau^{\left(i\right)}\right)\right)}$ (6.8)

（6.8）式给出的策略梯度是无偏的，但是方差很大。我们在回报中引入常数基线b来减小方差。

首先，证明当回报中引入常数b时，策略梯度不变即：

$\nabla_{\theta}U\left(\theta\right)\approx\hat{g}=\frac{1}{m}\sum_{i=1}^m{\nabla_{\theta}\log P\left(\tau^{\left(i\right)};\theta\right)R\left(\tau^{\left(i\right)}\right)}\]\[=\frac{1}{m}\sum_{i=1}^m{\nabla_{\theta}\log P\left(\tau^{\left(i\right)};\theta\right)\left(R\left(\tau^{\left(i\right)}\right)-b\right)}$

证明：

$E\left[\nabla_{\theta}\log P\left(\tau ;\theta\right)b\right]\]\[=\sum_{\tau}{P\left(\tau ;\theta\right)}\nabla_{\theta}\log P\left(\tau ;\theta\right)b\]\[=\sum_{\tau}{P\left(\tau ;\theta\right)}\frac{\nabla_{\theta}P\left(\tau ;\theta\right)b}{P\left(\tau ;\theta\right)}\]\[=\sum_{\tau}{\nabla_{\theta}P\left(\tau ;\theta\right)b}\]\[=\nabla_{\theta}\left(\sum_{\tau}{P\left(\tau ;\theta\right)}b\right)\]\[=\nabla_{\theta}b\]\[=0$

其次，我们求使得策略梯度的方差最小时的基线b

令 $X=\nabla_{\theta}\log P\left(\tau^{\left(i\right)};\theta\right)\left(R\left(\tau^{\left(i\right)}\right)-b\right)$ ，则方差为： $Var\left(X\right)=E\left(X-\bar{X}\right)^2=EX^2-E\bar{X}^2$

方差最小处，方差对b的导数为零，即：

$\frac{\partial Var\left(X\right)}{\partial b}=E\left(X\frac{\partial X}{\partial b}\right)=0$

其中 $\bar{X}=EX$ 与b无关。

将X带入，得到：

$b=\frac{\sum_{i=1}^m{\left[\left(\sum_{t=0}^H{\nabla_{\theta}\log\pi_{\theta}\left(u_{t}^{\left(i\right)}|s_{t}^{\left(i\right)}\right)}\right)^2R\left(\tau\right)\right]}}{\sum_{i=1}^m{\left[\left(\sum_{t=0}^H{\nabla_{\theta}\log\pi_{\theta}\left(u_{t}^{\left(i\right)}|s_{t}^{\left(i\right)}\right)}\right)^2\right]}}$ (6.9)

进一步减小方差的方法：修改回报函数：

引入基线后，策略梯度公式变为：

$\nabla_{\theta}U\left(\theta\right)\approx\frac{1}{m}\sum_{i=1}^m{\left(\sum_{t=0}^H{\nabla_{\theta}\log\pi_{\theta}\left(u_{t}^{\left(i\right)}|s_{t}^{\left(i\right)}\right)}\left(R\left(\tau^{\left(i\right)}\right)-b\right)\right)}$ (6.10)

其中，b取（6.9）式。我们对公式（6.10）进行进一步分析。在（6.10）中，每个动作 $u_{t}^{\left(i\right)}$ 所对应的 $\nabla_{\theta}\log\pi_{\theta}\left(u_{t}^{\left(i\right)}|s_{t}^{\left(i\right)}\right)$ 都乘以相同的该轨迹的总回报 $\left(R\left(\tau^{\left(i\right)}\right)-b\right)$ ，如图6.5所示。

图6.5 REINFORCE方法

然而，当前的动作与过去的回报实际上是没有关系的，即 $E_p\left[\partial_{\theta}\log\pi_{\theta}\left(u_t|x_t,t\right)r_j\right]=0\\ for\\ j<t$

因此，我们可以修改（6.10）中的回报函数。存在两种修改方法：

第一种称为（G(PO)MDP）:

$\nabla_{\theta}U\left(\theta\right)\approx\frac{1}{m}\sum_{i=1}^m{\sum_{j=0}^{H-1}{\left(\sum_{t=0}^j{\nabla_{\theta}\log\pi_{\theta}\left(u_{t}^{\left(i\right)}|s_{t}^{\left(i\right)}\right)\left(r_j-b_j\right)}\right)}}$

图6.6 G(PO)MDP方法

第二种称为策略梯度理论：

$\nabla_{\theta}U\left(\theta\right)\approx\frac{1}{m}\sum_{i=1}^m{\sum_{t=0}^{H-1}{\nabla_{\theta}\log\pi_{\theta}\left(u_{t}^{\left(i\right)}|s_{t}^{\left(i\right)}\right)}\left(\sum_{k=t}^{H-1}{\left(R\left(s_{k}^{\left(i\right)}\right)-b\right)}\right)}$

图6.7 策略梯度理论

为了使得方差最小，可以利用前面的方法求解相应的基线b。

0 0

强化学习进阶 第六讲 策略梯度方法

强化学习进阶第六讲策略梯度方法