特征值和特征向量（一）

来源：互联网发布：linux 守护进程的好处编辑：程序博客网时间：2024/06/05 18:36

作者：阿狸
链接：https://www.zhihu.com/question/21874816/answer/85155697
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

想要理解特征值，首先要理解矩阵相似。什么是矩阵相似呢？从定义角度就是：存在可逆矩阵P满足B＝ $P^{-1} AP$ 则我们说A和B是相似的。让我们来回顾一下之前得出的重要结论：对于同一个线性空间，可以用两组不同的基 $[\alpha ]$ 和基 $[\beta ]$ 来描述，他们之间的过渡关系是这样的： $[\beta ]=[\alpha ]P$ ，而对应坐标之间的过渡关系是这样的： $x_{2}=P^{-1}x_{1}$ 。其中P是可逆矩阵，可逆的意义是我们能变换过去也要能变换回来，这一点很重要。

我们知道，对于一个线性变换，只要你选定一组基，那么就可以用一个矩阵T1来描述这个线性变换。换一组基，就得到另一个不同的矩阵T2（之所以会不同，是因为选定了不同的基，也就是选定了不同的坐标系）。所有这些矩阵都是这同一个线性变换的描述，但又都不是线性变换本身。具体来说，有一个线性变换 $x_{1}\rightarrow y_{1}$ ，我们选择基 $[\alpha ]$ 来描述，对应矩阵是 $T_{1}$ ；同样的道理，我们选择基 $[\beta ]$ 来描述 $x_{2}\rightarrow y_{2}$ ，，对应矩阵是 $T_{2}$ ；我们知道基 $[\alpha ]$ 和基 $[\beta ]$ 是有联系的，那么他们之间的变换 $T_{1}$ 和 $T_{2}$ 有没有联系呢？

当然有， $T_{1}$ 和 $T_{2}$ 就是相似的关系，具体的请看下图：

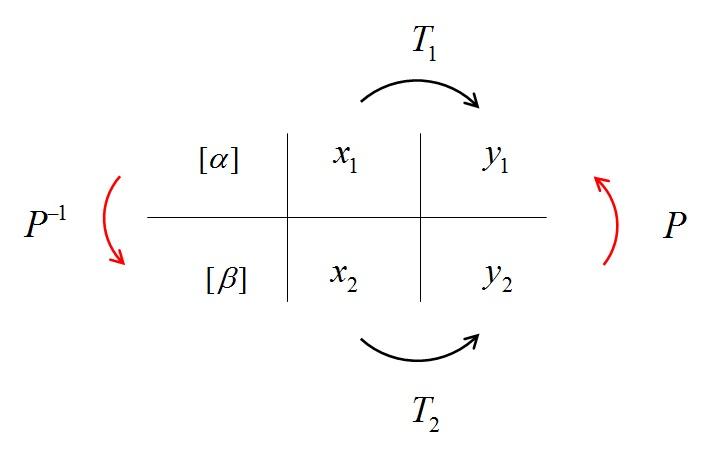
&lt;img src="https://pic1.zhimg.com/6cf43eca0f26cb1752f8fbf2633b699c_b.jpg" data-rawwidth="721" data-rawheight="449" class="origin_image zh-lightbox-thumb" width="721" data-original="https://pic1.zhimg.com/6cf43eca0f26cb1752f8fbf2633b699c_r.jpg"&gt;

没错，所谓相似矩阵，就是同一个线性变换的不同基的描述矩阵。这就是相似变换的几何意义。

这个发现太重要了。原来一族相似矩阵都是同一个线性变换的描述啊！难怪这么重要！工科研究生课程中有矩阵论、矩阵分析等课程，其中讲了各种各样的相似变换，比如什么相似标准型，对角化之类的内容，都要求变换以后得到的那个矩阵与先前的那个矩阵式相似的，为什么这么要求？因为只有这样要求，才能保证变换前后的两个矩阵是描述同一个线性变换的。就像信号处理（积分变换）中将信号（函数）进行拉氏变换，在复数域处理完了之后又进行拉式反变换，回到实数域一样。信号处理中是主要是为了将复杂的卷积运算变成乘法运算。其实这样的变换还有好多，有兴趣可以看积分变换的教材。

为什么这样做呢？矩阵的相似变换可以把一个比较丑的矩阵变成一个比较美的矩阵，而保证这两个矩阵都是描述了同一个线性变换。至于什么样的矩阵是“美”的，什么样的是“丑”的，我们说对角阵是美的。在线性代数中，我们会看到，如果把复杂的矩阵变换成对角矩阵，作用完了之后再变换回来，这种转换很有用处，比如求解矩阵的n次幂！而学了矩阵论之后你会发现，矩阵的n次幂是工程中非常常见的运算。这里顺便说一句，将矩阵对角化在控制工程和机械振动领域具有将复杂方程解耦的妙用！总而言之，相似变换是为了简化计算！

从另一个角度理解矩阵就是：矩阵主对角线上的元素表示自身和自身的关系，其他位置的元素aij表示i位置和j位置元素之间的相互关系。那么好，特征值问题其实就是选取了一组很好的基，就把矩阵 i位置和j位置元素之间的相互关系消除了。而且因为是相似变换，并没有改变矩阵本身的特性。因此矩阵对角化才如此的重要！

特征向量的引入是为了选取一组很好的基。空间中因为有了矩阵，才有了坐标的优劣。对角化的过程，实质上就是找特征向量的过程。如果一个矩阵在复数域不能对角化，我们还有办法把它化成比较优美的形式——Jordan标准型。高等代数理论已经证明：一个方阵在复数域一定可以化成Jordan标准型。这一点有兴趣的同学可以看一下高等代数后或者矩阵论。

经过上面的分析相信你已经可以得出如下结论了：坐标有优劣，于是我们选取特征向量作为基底，那么一个线性变换最核心的部分就被揭露出来——当矩阵表示线性变换时，特征值就是变换的本质！特征值的几何意义前面的答主已经用很多图解释过了，接下来我们分析一下特征值的物理意义：特征值英文名eigen value。“特征”一词译自德语的eigen，由希尔伯特在1904年首先在这个意义下使用（赫尔曼·冯·亥姆霍兹在更早的时候也在类似意义下使用过这一概念）。eigen一词可翻译为“自身的”，“特定于...的”，“有特征的”或者“个体的”—这强调了特征值对于定义特定的变换上是很重要的。它还有好多名字，比如谱，本征值。为什么会有这么多名字呢？

原因就在于他们应用的领域不同，中国人为了区分，给特不同的名字。你看英文文献就会发现，他们的名字都是同一个。当然，特征值的思想不仅仅局限于线性代数，它还延伸到其他领域。在数学物理方程的研究领域，我们就把特征值称为本征值。如在求解薛定谔波动方程时，在波函数满足单值、有限、连续性和归一化条件下，势场中运动粒子的总能量(正)所必须取的特定值，这些值就是正的本征值。

前面我们讨论特征值问题面对的都是有限维度的特征向量，下面我们来看看特征值对应的特征向量都是无限维函数的例子。这时候的特征向量我们称为特征函数，或者本证函数。这还要从你熟悉的微分方程说起。方程本质是一种约束，微分方程就是在世界上各种各样的函数中，约束出一类函数。对于一阶微分方程

$\frac{dy}{dt} =\lambda y$

我们发现如果我将变量y用括号[]包围起来，微分运算的结构和线性代数中特征值特征向量的结构,即 $\frac{d}{dt}[ y]=\lambda y$ 和 $T[y] =\lambda y$ 竟是如此相似。这就是一个求解特征向量的问题啊！只不过“特征向量”变成函数！我们知道只有 $e^{\lambda t}$ 满足这个式子。这里出现了神奇的数e，一杯开水放在室内，它温度的下降是指数形式的；听说过放射性元素的原子核发生衰变么？随着放射的不断进行，放射强度将按指数曲线下降；化学反应的进程也可以用指数函数描述……类似的现象还有好多。

为什么选择指数函数而不选择其他函数，因为指数函数是特征函数。为什么指数函数是特征？我们从线性代数的特征向量的角度来解释。这已经很明显了 $e^{\lambda t}$ 就是“特征向量”。于是，很自然的将线性代数的理论应用到线性微分方程中。那么指数函数就是微分方程（实际物理系统）的特征向量。用特征向量作为基表示的矩阵最为简洁。就像你把一个方阵经过相似对角化变换，耦合的矩阵就变成不耦合的对角阵一样。在机械振动里面所说的模态空间也是同样的道理。如果你恰巧学过振动分析一类的课程，也可以来和我交流。

同理，用特征函数解的方程也是最简洁的，不信你用级数的方法解方程，你会发现方程的解有无穷多项。解一些其他方程的时候(比如贝塞尔方程)我们目前没有找到特征函数，于是退而求其次才选择级数求解，至少级数具有完备性。实数的特征值代表能量的耗散或者扩散，比如空间中热量的传导、化学反应的扩散、放射性元素的衰变等。虚数的特征值(对应三角函数)代表能量的无损耗交换，比如空间中的电磁波传递、振动信号的动能势能等。复数的特征值代表既有交换又有耗散的过程，实际过程一般都是这样的。复特征值在电路领域以及振动领域将发挥重要的作用，可以说，没有复数，就没有现代的电气化时代！

对于二阶微分方程方程，它的解都是指数形式或者复指数形式。可以通过欧拉公式将其写成三角函数的形式。复特征值体现最多的地方是在二阶系统，别小看这个方程，整本自动控制原理都在讲它，整个振动分析课程也在讲它、还有好多课程的基础都是以这个微分方程为基础，这里我就不详细说了，有兴趣可以学习先关课程。说了这么多只是想向你传达一个思想，就是复指数函数式系统的特征向量！

如果将二阶微分方程转化成状态空间 $\frac{dx}{dt} =Ax$ 的形式(具体转化方法见现代控制理论，很简单的)

。则一个二阶线性微分方程就变成一个微分方程组的形式这时就出现了矩阵A，矩阵可以用来描述一个系统：如果是振动问题，矩阵A的特征值是虚数，对应系统的固有频率，也就是我们常说的，特征值代表振动的谱。如果含有耗散过程，特征值是负实数，对应指数衰减；特征值是正实数，对应指数发散过程，这时是不稳定的，说明系统极容易崩溃，如何抑制这种发散就是控制科学研究的内容。

提到振动的谱，突然想到了这个经典的例子：美国数学家斯特让（G..Strang）在其经典教材《线性代数及其应用》中这样介绍了特征值作为频率的物理意义，他说："大概最简单的例子（我从不相信其真实性，虽然据说1831年有一桥梁毁于此因）是一对士兵通过桥梁的例子。传统上，他们要停止齐步前进而要散步通过。这个理由是因为他们可能以等于桥的特征值之一的频率齐步行进，从而将发生共振。就像孩子的秋千那样，你一旦注意到一个秋千的频率，和此频率相配，你就使频率荡得更高。一个工程师总是试图使他的桥梁或他的火箭的自然频率远离风的频率或液体燃料的频率；而在另一种极端情况，一个证券经纪人则尽毕生精力于努力到达市场的自然频率线。特征值是几乎任何一个动力系统的最重要的特征。"

&lt;img src="https://pic2.zhimg.com/0a02c56afda30b25d653ae4e24629d5d_b.jpg" data-rawwidth="395" data-rawheight="216" class="content_image" width="395"&gt;

对于一个线性系统，总可以把高阶的方程转化成一个方程组描述，这被称为状态空间描述。因此，他们之间是等价的。特征值还有好多用处，原因不在特征值本身，而在于特征值问题和你的物理现象有着某种一致的对应关系。学习特征值问题告诉你一种解决问题的方法：寻找事物的特征，然后特征分解。

最后声明一下，本文是在整理孟岩老师的《理解矩阵》和任广千、胡翠芳老师的《线性代数的几何意义》基础上形成的，只是出于一种对数学的爱好！有兴趣的读者建议阅读原文。也欢迎下载《神奇的矩阵》和《神奇的矩阵第二季》了解更多有关线性代数和矩阵的知识。

0 0