旋转矩阵和角速度的一些应用
来源:互联网 发布:什么是域名根目录 编辑:程序博客网 时间:2024/05/21 22:24
科里奧利力、離心力和歐拉力是由於坐標系旋轉引起的假象力。設全局坐標系A(又稱慣性系)原點(Origin)為O,局部坐標系B(又稱非慣性系)原點為o,旋轉矩陣為R.
在全局坐標系下點P(X,Y,Z)由R變換到局部坐標系下p(x,y,z)的表達式如下:
P=Rp
這裡P和p是一個點,只不過參考系不同,表現出來的坐標也不同。p跟隨坐標系B運動。
對上面的位置函數二次求導就能得到慣性力的公式。
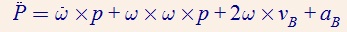
在全局坐標系下點P(X,Y,Z)由R變換到局部坐標系下p(x,y,z)的表達式如下:
P=Rp
這裡P和p是一個點,只不過參考系不同,表現出來的坐標也不同。p跟隨坐標系B運動。
對上面的位置函數二次求導就能得到慣性力的公式。
假定旋轉參照系B的角速度為Omega, 方向由右手定則確定。

準備
首先證明在參照系變換中, 。
。
這裡的D表示是在慣性坐標系下求導。前一項表示大小變化,後一項表示方向變化)這個公式在很多材料中一筆帶過,是十分有價值的結論。
定義 是某向量Q在慣性系下的微分。
是某向量Q在慣性系下的微分。
定義 是某向量Q在非慣性系下的微分。
是某向量Q在非慣性系下的微分。
設B中的單位正交向量為e1, e2, e3。

因為第二項的e在B系中是固定的,在A中不是,而是以omega為角速度旋轉,有

上式另外一種推導如下:

這裡把R看作了無窮小矩陣。

所以有:

推導
假設坐標系統 B 在 A 中的單位軸為 uj, j = { 1 , 2 , 3 } , 把旋轉等變換附著在這三個單位軸上 , 如上節所說

T是平動位移。

假設僅僅是轉動,平動加速度為零:

以上是從慣性系觀察的結果,而從非慣性系中觀看:

旋轉矩陣的進一步分析
三維下的旋轉矩陣在特定條件下使用三個數字就能表示,這是因為旋轉矩陣只改變向量方向,不改變大小,所以旋轉前後內積不變:

所以

也可以記為:

另一種推導
用矩陣表示向量叉積
因為

上述3乘3矩陣是一個反對稱矩陣,這裡也可稱為叉積矩陣。
用叉 乘矩陣可以很方便地表示旋轉矩陣的導數。
假設B中有固定點l, 在L=Rl中對R求導:

證明如下:

一個有趣的驗證法是假定一個旋轉代入:

與R的導數結果相同。
下面分析P=Rp的情況:

所以:

注意這裡微分的時候,時間間隔很小,所以

接近於零,R近似於單位陣。因此:
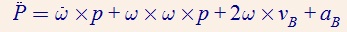
0 0
- 旋转矩阵和角速度的一些应用
- 旋转矩阵和角速度的一些应用
- 角速度与旋转矩阵的转换关系及思考
- 关于协方差矩阵和相关系数矩阵的一些应用认识
- 矩阵在CSS3 3D旋转和2D旋转上的应用
- 旋转矩阵和旋转向量
- 旋转矩阵的理解和使用
- 矩阵的平移,缩放和旋转
- 欧拉角和旋转矩阵的转换
- 旋转向量和旋转矩阵的互转换
- 旋转矩阵和平移矩阵
- 旋转矩阵和变换矩阵
- 四元数和旋转矩阵
- 四元数和旋转矩阵
- 四元数和旋转矩阵
- 笛卡尔坐标系的旋转矩阵在OpenGL坐标系的应用
- 六轴系统中陀螺仪输出的角速度的一些问题
- 2559矩阵的旋转
- Git(3)——创建版本库
- c语言编程题目(一)
- 山东省第八届acm省赛C题 巨坑
- ubuntu系统常用软件的安装及常见问题解决办法
- 远程传输工具
- 旋转矩阵和角速度的一些应用
- 机器学习概念速查
- Git(4)——把文件添加并提交到版本库
- 接口和抽象类有什么区别
- Leetcode学习(39)—— Majority Element
- poj-1502(最短路dijkstra算法)
- 排序算法之插入排序
- HTML学习笔记
- windows防火墙无法启动0x8007042c解决办法


