优化算法——拟牛顿法之DFP算法
来源:互联网 发布:洛阳中国联合网络通信 编辑:程序博客网 时间:2024/05/17 06:20
一、牛顿法
在博文“优化算法——牛顿法(Newton Method)”中介绍了牛顿法的思路,牛顿法具有二阶收敛性,相比较最速下降法,收敛的速度更快。在牛顿法中使用到了函数的二阶导数的信息,对于函数) ,其中
,其中 表示向量。在牛顿法的求解过程中,首先是将函数
表示向量。在牛顿法的求解过程中,首先是将函数) 在
在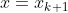 处展开,展开式为:
处展开,展开式为:
其中,) ,表示的是目标函数在
,表示的是目标函数在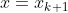 的梯度,是一个向量。
的梯度,是一个向量。) ,表示的是目标函数在
,表示的是目标函数在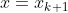 处的Hesse矩阵。省略掉最后面的高阶无穷小项,即为:
处的Hesse矩阵。省略掉最后面的高阶无穷小项,即为:
上式两边对 求导,即为:
求导,即为:
在基本牛顿法中,取得最值的点处的导数值为 ,即上式左侧为
,即上式左侧为 。则:
。则:
求出其中的 :
:
从上式中发现,在牛顿法中要求Hesse矩阵是可逆的。
当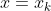 时,上式为:
时,上式为:
此时,是否可以通过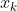 ,
,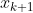 ,
,) 和
和) 模拟出Hesse矩阵的构造过程?此方法便称为拟牛顿法(QuasiNewton),上式称为拟牛顿方程。在拟牛顿法中,主要包括DFP拟牛顿法,BFGS拟牛顿法。
模拟出Hesse矩阵的构造过程?此方法便称为拟牛顿法(QuasiNewton),上式称为拟牛顿方程。在拟牛顿法中,主要包括DFP拟牛顿法,BFGS拟牛顿法。
二、DFP拟牛顿法
1、DFP拟牛顿法简介
DFP拟牛顿法也称为DFP校正方法,DFP校正方法是第一个拟牛顿法,是有Davidon最早提出,后经Fletcher和Powell解释和改进,在命名时以三个人名字的首字母命名。
对于拟牛顿方程:
化简可得:
令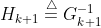 ,可以得到:
,可以得到:
在DFP校正方法中,假设:
2、DFP校正方法的推导
令: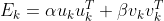 ,其中
,其中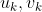 均为
均为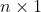 的向量。
的向量。-\bigtriangledown&space;f\left&space;(&space;x_k&space;\right&space;)) ,
,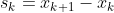 。
。
则对于拟牛顿方程![H_{k+1}\left [ \bigtriangledown f\left ( x_{k+1} \right )-\bigtriangledown f\left ( x_k \right ) \right ]=x_{k+1}-x_k](http://latex.codecogs.com/gif.latex?H_{k+1}\left&space;[&space;\bigtriangledown&space;f\left&space;(&space;x_{k+1}&space;\right&space;)-\bigtriangledown&space;f\left&space;(&space;x_k&space;\right&space;)&space;\right&space;]=x_{k+1}-x_k) 可以简化为:
可以简化为:
将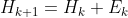 代入上式:
代入上式:
将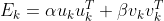 代入上式:
代入上式:
已知: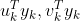 为实数,
为实数,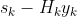 为
为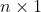 的向量。上式中,参数
的向量。上式中,参数 和
和 解的可能性有很多,我们取特殊的情况,假设
解的可能性有很多,我们取特殊的情况,假设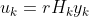 ,
,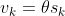 。则:
。则:

代入上式:
令&space;+1=0) ,
,&space;-1=0) ,则:
,则:
则最终的DFP校正公式为:
3、DFP拟牛顿法的算法流程
设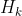 对称正定,
对称正定,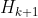 由上述的DFP校正公式确定,那么
由上述的DFP校正公式确定,那么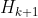 对称正定的充要条件是
对称正定的充要条件是 。
。
在博文“优化算法——牛顿法(Newton Method)”中介绍了非精确的线搜索准则:Armijo搜索准则,搜索准则的目的是为了帮助我们确定学习率,还有其他的一些准则,如Wolfe准则以及精确线搜索等。在利用Armijo搜索准则时并不是都满足上述的充要条件,此时可以对DFP校正公式做些许改变:
DFP拟牛顿法的算法流程如下:

4、求解具体的优化问题
求解无约束优化问题
其中,^T\in\mathbb{R}^2) 。
。
python程序实现:
- function.py
- dfp.py
- testDFP.py
5、实验结果

阅读全文
0 0
- 优化算法——拟牛顿法之DFP算法
- 优化算法——拟牛顿法之DFP算法
- 优化算法——拟牛顿法之DFP
- 拟牛顿法之DFP算法
- 拟牛顿法之DFP算法
- 最优化学习笔记(十八)——拟牛顿法(4)DFP算法
- 拟牛顿法中的DFP算法和BFGS算法
- 拟牛顿法、DFP算法及BFGS算法
- 优化算法——拟牛顿法之BFGS算法
- 优化算法——拟牛顿法之BFGS算法
- 优化算法——牛顿法和拟牛顿法
- 牛顿法与拟牛顿法学习笔记(三)DFP 算法
- 牛顿法与拟牛顿法学习笔记(三)DFP 算法
- 牛顿法与拟牛顿法学习笔记(三)DFP 算法
- 牛顿法与拟牛顿法学习笔记(三)DFP 算法
- 牛顿法与拟牛顿法学习笔记(三)DFP 算法
- 牛顿法与拟牛顿法学习笔记(三)DFP 算法
- 牛顿法与拟牛顿法学习笔记(三)DFP 算法
- ORACLE中数据查重及重复数据删除
- 欢迎使用CSDN-markdown编辑器
- SPRINGMYBATIS01 Unit05: 实战技巧 、 资费列表 、 拦截器
- WebRoot和WebContenct有什么区别
- Rails 中 scope
- 优化算法——拟牛顿法之DFP算法
- CentOS 7 用yum安装各种必需
- Python中Unicode字符串
- java 2 带有小数的进制转换
- js监听滚动条事件和获取浏览器及屏幕高度和宽度等信息的方法
- 数据库索引工作原理
- Android Studio MVP 构建模板
- 接口的例子代码
- 关于iOS原生条形码扫描,你需要注意的两三事


