优化算法——拟牛顿法之DFP算法
来源:互联网 发布:苏州园区网络托管 编辑:程序博客网 时间:2024/04/30 06:30
一、牛顿法
在博文“优化算法——牛顿法(Newton Method)”中介绍了牛顿法的思路,牛顿法具有二阶收敛性,相比较最速下降法,收敛的速度更快。在牛顿法中使用到了函数的二阶导数的信息,对于函数) ,其中
,其中 表示向量。在牛顿法的求解过程中,首先是将函数
表示向量。在牛顿法的求解过程中,首先是将函数) 在
在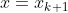 处展开,展开式为:
处展开,展开式为:
其中,) ,表示的是目标函数在
,表示的是目标函数在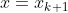 的梯度,是一个向量。
的梯度,是一个向量。) ,表示的是目标函数在
,表示的是目标函数在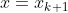 处的Hesse矩阵。省略掉最后面的高阶无穷小项,即为:
处的Hesse矩阵。省略掉最后面的高阶无穷小项,即为:
上式两边对 求导,即为:
求导,即为:
在基本牛顿法中,取得最值的点处的导数值为 ,即上式左侧为
,即上式左侧为 。则:
。则:
求出其中的 :
:
从上式中发现,在牛顿法中要求Hesse矩阵是可逆的。
当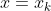 时,上式为:
时,上式为:
此时,是否可以通过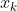 ,
,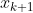 ,
,) 和
和) 模拟出Hesse矩阵的构造过程?此方法便称为拟牛顿法(QuasiNewton),上式称为拟牛顿方程。在拟牛顿法中,主要包括DFP拟牛顿法,BFGS拟牛顿法。
模拟出Hesse矩阵的构造过程?此方法便称为拟牛顿法(QuasiNewton),上式称为拟牛顿方程。在拟牛顿法中,主要包括DFP拟牛顿法,BFGS拟牛顿法。
二、DFP拟牛顿法
1、DFP拟牛顿法简介
DFP拟牛顿法也称为DFP校正方法,DFP校正方法是第一个拟牛顿法,是有Davidon最早提出,后经Fletcher和Powell解释和改进,在命名时以三个人名字的首字母命名。
对于拟牛顿方程:
化简可得:
令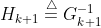 ,可以得到:
,可以得到:
在DFP校正方法中,假设:
2、DFP校正方法的推导
令: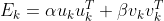 ,其中
,其中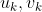 均为
均为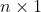 的向量。
的向量。-\bigtriangledown&space;f\left&space;(&space;x_k&space;\right&space;)) ,
,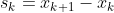 。
。
则对于拟牛顿方程![H_{k+1}\left [ \bigtriangledown f\left ( x_{k+1} \right )-\bigtriangledown f\left ( x_k \right ) \right ]=x_{k+1}-x_k](http://latex.codecogs.com/gif.latex?H_{k+1}\left&space;[&space;\bigtriangledown&space;f\left&space;(&space;x_{k+1}&space;\right&space;)-\bigtriangledown&space;f\left&space;(&space;x_k&space;\right&space;)&space;\right&space;]=x_{k+1}-x_k) 可以简化为:
可以简化为:
将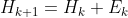 代入上式:
代入上式:
将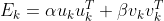 代入上式:
代入上式:
已知: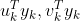 为实数,
为实数,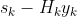 为
为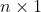 的向量。上式中,参数
的向量。上式中,参数 和
和 解的可能性有很多,我们取特殊的情况,假设
解的可能性有很多,我们取特殊的情况,假设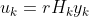 ,
,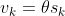 。则:
。则:

代入上式:
令&space;+1=0) ,
,&space;-1=0) ,则:
,则:
则最终的DFP校正公式为:
3、DFP拟牛顿法的算法流程
设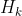 对称正定,
对称正定,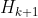 由上述的DFP校正公式确定,那么
由上述的DFP校正公式确定,那么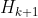 对称正定的充要条件是
对称正定的充要条件是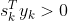 。
。
在博文“优化算法——牛顿法(Newton Method)”中介绍了非精确的线搜索准则:Armijo搜索准则,搜索准则的目的是为了帮助我们确定学习率,还有其他的一些准则,如Wolfe准则以及精确线搜索等。在利用Armijo搜索准则时并不是都满足上述的充要条件,此时可以对DFP校正公式做些许改变:
DFP拟牛顿法的算法流程如下:

4、求解具体的优化问题
求解无约束优化问题
其中,^T\in\mathbb{R}^2) 。
。
python程序实现:
- function.py
#coding:UTF-8'''Created on 2015年5月19日@author: zhaozhiyong'''from numpy import *#fundef fun(x): return 100 * (x[0,0] ** 2 - x[1,0]) ** 2 + (x[0,0] - 1) ** 2#gfundef gfun(x): result = zeros((2, 1)) result[0, 0] = 400 * x[0,0] * (x[0,0] ** 2 - x[1,0]) + 2 * (x[0,0] - 1) result[1, 0] = -200 * (x[0,0] ** 2 - x[1,0]) return result
- dfp.py
#coding:UTF-8'''Created on 2015年5月19日@author: zhaozhiyong'''from numpy import *from function import *def dfp(fun, gfun, x0): result = [] maxk = 500 rho = 0.55 sigma = 0.4 m = shape(x0)[0] Hk = eye(m) k = 0 while (k < maxk): gk = mat(gfun(x0))#计算梯度 dk = -mat(Hk)*gk m = 0 mk = 0 while (m < 20): newf = fun(x0 + rho ** m * dk) oldf = fun(x0) if (newf < oldf + sigma * (rho ** m) * (gk.T * dk)[0,0]): mk = m break m = m + 1 #DFP校正 x = x0 + rho ** mk * dk sk = x - x0 yk = gfun(x) - gk if (sk.T * yk > 0): Hk = Hk - (Hk * yk * yk.T * Hk) / (yk.T * Hk * yk) + (sk * sk.T) / (sk.T * yk) k = k + 1 x0 = x result.append(fun(x0)) return result
- testDFP.py
#coding:UTF-8'''Created on 2015年5月19日@author: zhaozhiyong'''from bfgs import *from dfp import dfpimport matplotlib.pyplot as plt x0 = mat([[-1.2], [1]])result = dfp(fun, gfun, x0)n = len(result)ax = plt.figure().add_subplot(111)x = arange(0, n, 1)y = resultax.plot(x,y)plt.show()
5、实验结果

0 0
- 优化算法——拟牛顿法之DFP算法
- 优化算法——拟牛顿法之DFP算法
- 优化算法——拟牛顿法之DFP
- 拟牛顿法之DFP算法
- 拟牛顿法之DFP算法
- 最优化学习笔记(十八)——拟牛顿法(4)DFP算法
- 拟牛顿法中的DFP算法和BFGS算法
- 拟牛顿法、DFP算法及BFGS算法
- 优化算法——拟牛顿法之BFGS算法
- 优化算法——拟牛顿法之BFGS算法
- 优化算法——牛顿法和拟牛顿法
- 牛顿法与拟牛顿法学习笔记(三)DFP 算法
- 牛顿法与拟牛顿法学习笔记(三)DFP 算法
- 牛顿法与拟牛顿法学习笔记(三)DFP 算法
- 牛顿法与拟牛顿法学习笔记(三)DFP 算法
- 牛顿法与拟牛顿法学习笔记(三)DFP 算法
- 牛顿法与拟牛顿法学习笔记(三)DFP 算法
- 牛顿法与拟牛顿法学习笔记(三)DFP 算法
- 第10周项目2-1职员有薪水了
- 在Ubuntu下进行MongoDB安装步骤
- LinkedList源码分析
- NGUI之UITab Bar的不能将Sprite与SelectedSprite设置成相同的精灵
- SpringMVC-07 mvc:annotation-driven
- 优化算法——拟牛顿法之DFP算法
- VM中安装CentOS
- # Android Activity 的生命周期
- OC的方法和 函数
- 【Java心得总结三-----初识泛型】
- #笔记#圣思园 JavaSE 第48讲——Map映射
- 课堂作业1
- POJ2406寻找循环节
- NSUserDefaults重置数据


