01背包和完全背包

01背包：

有N件物品和一个容量为V的背包。第i件物品的费用是c[i]，价值是w[i]。求解将哪些物品装入背包可使价值总和最大。

从这个题目中可以看出，01背包的特点就是：每种物品仅有一件，可以选择放或不放。

其状态转移方程是：

dp[i][v]=max{f[i-1][v],f[i-1][v-c[i]]+w[i]}

对于这方方程其实并不难理解，方程之中，现在需要放置的是第i件物品，这件物品的体积是c[i],价值是w[i],因此f[i-1][v]代表的就是不将这件物品放入背包，而f[i-1][v-c[i]]+w[i]则是代表将第i件放入背包之后的总价值，比较两者的价值，得出最大的价值存入现在的背包之中。

理解了这个方程后，将方程代入实际题目的应用之中，可得

for(i = 1; i<=n; i++)  {      for(j = v; j>=c[i]; j--)//在这里，背包放入物品后，容量不断的减少，直到再也放不进了      {          f[i][v]=max(f[i-1][v],f[i-1][v-c[i]]+w[i]);      }  } 

以下直接给出优化后的代码：
//求解将哪些物品装入背包可使这些物品的重量总和不超过背包承重量t，且价值总和最大。

#include <stdio.h>#include <string.h>int f[1010],w[1010],v[1010];//f记录不同承重量背包的总价值，w记录不同物品的重量，v记录不同物品的价值int max(int x,int y){//返回x,y的最大值    if(x>y) return x;    return y;}int main(){    int t,m,i,j;    memset(f,0,sizeof(f));  //总价值初始化为0    scanf("%d %d",&t,&m);  //输入背包承重量t、物品的数目m    for(i=1;i<=m;i++)        scanf("%d %d",&w[i],&v[i]);  //输入m组物品的重量w[i]和价值v[i]    for(i=1;i<=m;i++){  //尝试放置每一个物品        for(j=t;j>=w[i];j--){//倒叙是为了保证每个物品都使用一次            f[j]=max(f[j-w[i]]+v[i],f[j]);            //在放入第i个物品前后，检验不同j承重量背包的总价值，如果放入第i个物品后比放入前的价值提高了，则修改j承重量背包的价值，否则不变        }    }    printf("%d",f[t]);  //输出承重量为t的背包的总价值    printf("\n");    getch();    return 0;}

完全背包：

　完全背包：有N种物品和一个容量为V的背包，每种物品都有无限件可用。第i种物品的费用是c[i]，价值是w[i]。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量，且价值总和最大。　　
　根据第i种物品放多少件进行决策，所以状态转移方程为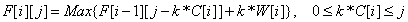

   　　其中F[i-1][j-K*C[i]]+K*W[i]表示前i-1种物品中选取若干件物品放入剩余空间为j-K*C[i]的背包中所能得到的最大价值加上k件第i种物品；   　　设物品种数为N，背包容量为V，第i种物品体积为C[i]，第i种物品价值为W[i]。   　　与01背包相同，完全背包也需要求出NV个状态F[i][j]。但是完全背包求F[i][j]时需要对k分别取0,…，j/C[i]求最大F[i][j]值。

很明显，这样一般情况下会超时，需要转化成时间复杂度比较低的在进行求解

　　经过思考可以想到完全背包可以转化为01背包：

   因为同种物品可以多次选取，那么第i种物品最多可以选取V/C[i]件价值不变的物品，然后就转化为01背包问题。如果把第i种物品拆成体积为C[i]×2k价值W[i]×2k的物品，其中满足C[i]×2k≤V。即设F[i][j]表示出在前i种物品中选取若干件物品放入容量为j的背包所得的最大价值。那么对于第i种物品的出现，我们对第i种物品放不放入背包进行决策。如果不放那么F[i][j]=F[i-1][j]；如果确定放，背包中应该出现至少一件第i种物品，所以F[i][j]种至少应该出现一件第i种物品,即F[i][j]=F[i][j-C[i]]+W[i]。为什么会是F[i][j-C[i]]+W[i]？因为F[i][j-C[i]]里面可能有第i种物品，也可能没有第i种物品。我们要确保F[i][j]至少有一件第i件物品，所以要预留C[i]的空间来存放一件第i种物品。

　　状态方程为：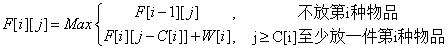

#include<cstdio>#include<algorithm>using namespace std;int w[300],c[300],f[300010];int V,n;int main(){    scanf("%d%d",&V,&n);    for(int i=1; i<=n; i++)    {        scanf("%d%d",&w[i],&c[i]);    }    for(int i=1; i<=n; i++)        for(int j=w[i]; j<=V; j++)//注意此处，与0-1背包不同，这里为顺序，0-1背包为逆序            f[j]=max(f[j],f[j-w[i]]+c[i]);    printf("max=%d\n",f[V]);    return 0;}

　0-1背包和完全背包的不同：

　　从二维数组上区别0-1背包和完全背包也就是状态转移方程就差别在放第i中物品时，完全背包在选择放这个物品时，最优解是F[i][j-c[i]]+w[i]即画表格中同行的那一个，而0-1背包比较的是F[i-1][j-c[i]]+w[i]，上一行的那一个。

　　从一维数组上区别0-1背包和完全背包差别就在循环顺序上，0-1背包必须逆序，因为这样保证了不会重复选择已经选择的物品，而完全背包是顺序，顺序会覆盖以前的状态，所以存在选择多次的情况，也符合完全背包的题意。状态转移方程都为F[i] = max(F[i],dp[F-c[i]]+v[i])。